算額（その112）

算額（その112）

愛媛県松山市 伊佐爾波神社 嘉永3年(1850)5月
http://www.wasan.jp/ehime/isaniwa14.html

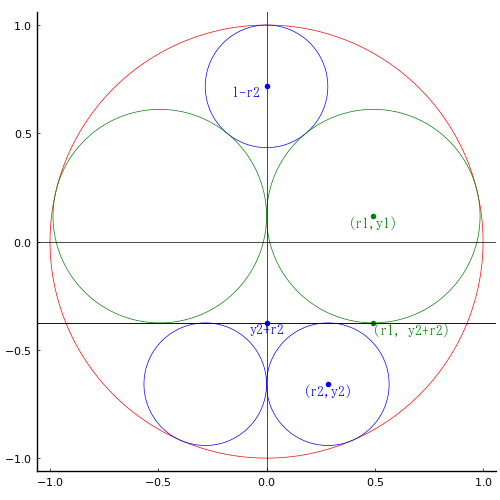
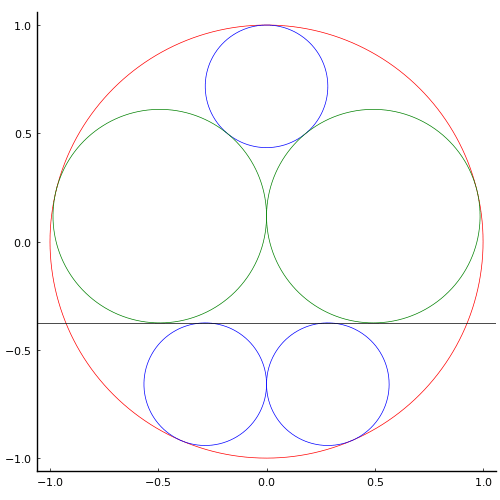
円内に 2 つの甲円，3 つの乙円が入っている。それぞれの円の半径を求めよ。

算額（その111）に似ているのだが，写真が不鮮明であるが，下の 2 つの乙円と甲円がそれぞれ直線に接している。

外円の半径を 1 とする。甲円，乙円の中心座標と半径を (r1, y1, r1)，(r2, y2, r2) とおき，以下の方程式を立てて解く。
算額（その111）と違うのは eq4 である。しょうもない条件であるが，これでは以下のように無意味な解しか得られない。

using SymPy
@syms r1, r2, y1, y2;
eq3 = r1^2 + (1 - r2 - y1)^2 - (r1 + r2)^2 |> expand
eq4 = y1 - (y2 + r2) - r1
eq5 = r1^2 + y1^2 - (1 - r1)^2 |> expand
eq6 = r2^2 + y2^2 - (1 - r2)^2 |> expand;

solve([eq3, eq4, eq5, eq6], (r1, r2, y1, y2))

   1-element Vector{NTuple{4, Sym}}:
    (0, 0, 1, 1)

そこで， nlsolve() で数値解を求めることにする。

eq3 |> println
eq4 |> println
eq5 |> println
eq6 |> println

   -2*r1*r2 + 2*r2*y1 - 2*r2 + y1^2 - 2*y1 + 1
   -r1 - r2 + y1 - y2
   2*r1 + y1^2 - 1
   2*r2 + y2^2 - 1

using NLsolve

function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;

function H(u)
  (r1, r2, y1, y2) = u
  return [
       -2*r1*r2 + 2*r2*y1 - 2*r2 + y1^2 - 2*y1 + 1,
       -r1 - r2 + y1 - y2,
       2*r1 + y1^2 - 1,
       2*r2 + y2^2 - 1
   ]
end;

iniv = [0.5, 0.3, 0.1, -0.6]
res = nls(H, ini=iniv)
println(res)

ちゃんと解が求まった。

   ([0.49309632821478017, 0.28307747532588534, 0.11750465339908704, -0.6586691501415785], true)

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, y1, y2) = [0.49309632821478017, 0.28307747532588534, 0.11750465339908704, -0.6586691501415785]
   plot()
   circle(0, 0, 1)
   circle(r2, y2, r2, :blue)
   circle(-r2, y2, r2, :blue)
   circle(0, 1 - r2, r2, :blue)
   circle(r1, y1, r1, :green)
   circle(-r1, y1, r1, :green)
   hline!([y2+r2], color=:black, lw=0.5)
   if more == true
       @printf("r1 = %.5f; r2 = %.5f;  y1 = %.5f;  y2 = %.5f", r1, r2, y1, y2)
       point(r1, y1, "(r1,y1)", :green, :center)
       point(0, 1 - r2, "1-r2 ", :blue, :right)
       point(r2, y2, "(r2,y2)", :blue, :center)
       point(0, y2+r2, "y2+r2", :blue, :center)
       point(r1, y2+r2, "(r1, y2+r2)")
       hline!([0, y2+r2], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   end
end;

   r1 = 0.49310; r2 = 0.28308;  y1 = 0.11750;  y2 = -0.65867