算額（その1109）

算額（その1109）

四十一 岩手県一関市牧沢 牧沢八幡神社 明治8年(1875)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円5個，外円，弦

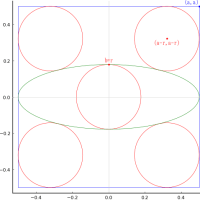
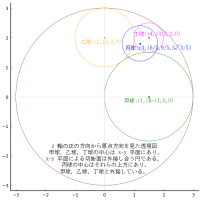
全円の中に弦を引き，その上下に 4 個の等円を容れる。等円の直径が 1 寸のとき，全円の直径はいかほどか。

注：弦の傾斜をどのようにしようとも，弦の上下（両側）は対称，すなわち弦は全円の直径であり，弦の傾斜はどのようにしても同じ図形になる（図を回転すれば弦は水平にできる）。弦を水平にすれば，4 個の等円はそれぞれが x 軸，y 軸に接する。

全円の半径と中心座標を R, (0, 0)
第一象限にある等円の半径と中心座標を r, (r1, r1)
とおき，以下の方程式を解く。

include("julia-source.txt")

using SymPy
@syms R::positive, r::positive
eq1 = 2r^2 - (R - r)^2
res = solve(eq1, R)[1]
res |> println

   r*(1 + sqrt(2))

全円の半径 R は等円の半径 r の 1 + √2 倍である。
等円の直径が 1 寸のとき，全円の直径は 2.414213562373095 寸である。

「答」には「全円の径二寸六分一厘八毛有奇」とあり，「術」には「置一ケ二分5厘開平方余加一ケ五分乗等径得全円径」とある。
つまり，等円の径を √1.25 + 1.5 = 2.618033988749895 倍すれば全円径が得られるというのだが，山村もなんの疑問も呈していない。
山村とわたし，どちらが間違っているのか?

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   R = r*(1 + √2)
   @printf("等円の直径が %g のとき，全円の直径は %g である。\n", 2r, 2R)
   plot()
   circle(0, 0, R)
   rotate(√2r*cosd(67.5), √2r*sind(67.5), r, :blue, angle=90)
   segment(R*cosd(22.5), R*sind(22.5), R*cosd(202.5), R*sind(202.5), :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(√2r*cosd(67.5), √2r*sind(67.5), "等円:r", :blue, :center, delta=-delta/2)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
   end
end;