「Excel 方眼紙はこんな時に役に立つ《Excel 方眼紙を究める》」だけど，マジかよ...
ここにも，お笑いのネタが埋蔵されている。
> 実はExcelは優れた文書作成ツールであり
> 「Excel方眼紙」とすることで、使いやすさはさらに高まる
> 罫線やセルの結合などの機能を使い、自由に表を作成できる
弱点もあると認めているが、だから止めようなんてつゆほども思っていない。
> 複雑な構造の文書を作成したとき、ほかの人がどう再編集したらよいかが一見しただけでは分かりにくい。同僚や取引先と共有するなら複雑な構造は控えるなど、配慮が必要な場合もある
> 入力したデータの再利用がしづらくなる
「効果量でものを言え」といってもね...
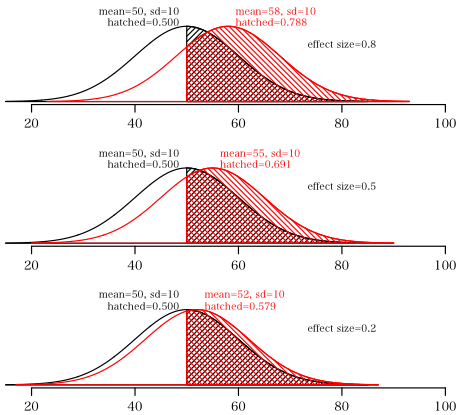
効果量大，中，小が 0.8, 0.5, 0.2 ということは，図に示すように明らかなことなんだけど，
対照群（平均値=50，標準偏差=10）のとき，処置群（平均値=58, 55, 52, 標準偏差=10）なわけで，
対照群では平均値以上のものの割合は 50% であるが，処置群では対照群の平均値より大きいものの割合はそれぞれ 78.8%, 69.1%，57.9% と確かに多いわけではあるが...
それらは，対照群に比べて実質的にどれくらい優れていると評価できるのか？
効果量が 0.2 程度の制がん剤は意味があるのか？おそらく無いであろう。
しかも，社会学や心理学のように，サンプルサイズをふんだんに確保することなんかできないのだから。
そんな場合には，サンプルサイズを考慮して評価せざるを得ないだろう。つまり，究極的には検定だ。
appendix
上の図を描いたプログラム
draw = function(mean=50, sd=10, cp=50, col=1, angle=45, density=30, pos=2) {
lo = mean-3.5*sd
hi = mean+3.5*sd
x = seq(lo, hi, length=1000)
y = dnorm(x, mean, sd)
lines(c(x, hi, lo), c(y, 0, 0), col=col)
x = seq(cp, hi, length=1000)
y = dnorm(x, mean, sd)
polygon(c(x, hi, cp), c(y, 0, 0), col=col, angle=angle, density=density)
text(mean, 0.047, sprintf("mean=%i, sd=%i", mean, sd), col=col, pos=pos, xpd=TRUE, cex=0.8)
text(mean, 0.041, sprintf("hatched=%.3f", pnorm(50, mean=mean, sd=sd, lower.tail=FALSE)), xpd=TRUE, col=col, pos=pos, cex=0.8)
}
draw2 = function(mean=58) {
plot(0, 0, xlim=c(15, 100), ylim=c(0,0.04), type="n", xlab="score", ylab="", bty="n", yaxt="n")
draw()
draw(mean=mean, col=2, angle=135, pos=4)
text(80, 0.03, sprintf("effect size=%.1f", (mean-50)/10), cex=0.8)
}
layout(matrix(1:3, 3))
old=par(mgp=c(1.8, 0.8, 0), mar=c(2, 2, 2, 1))
draw2(58)
draw2(55)
draw2(52)
par(old)
layout(1)
