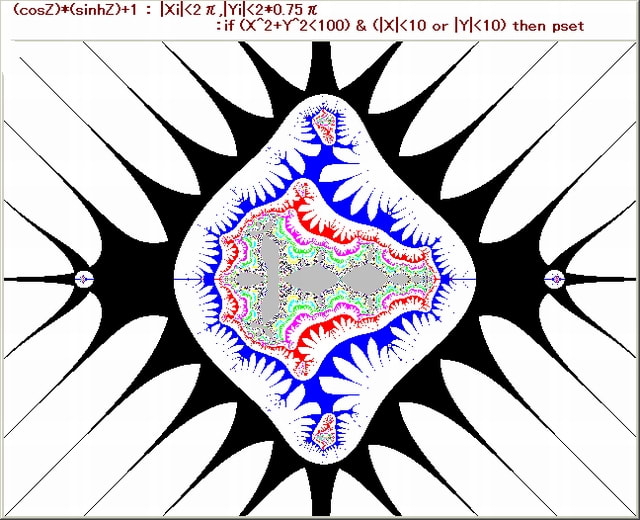
下図の画像の作成条件は、以下のとおり。
1. 複素関数:Z^2*sinZ+0.46。
2. N-loop脱出条件:Q=1/(log|X|log|Y|),(|Q|>10 or |Q|<0.1)
3. pset条件:|X|<10 or |Y|<10
4. 色設定:N-loop貫通時はC=15。N-loop脱出時は其の時のNをNoとすると C=No mod 16,C=7→8
5. Nmax=50

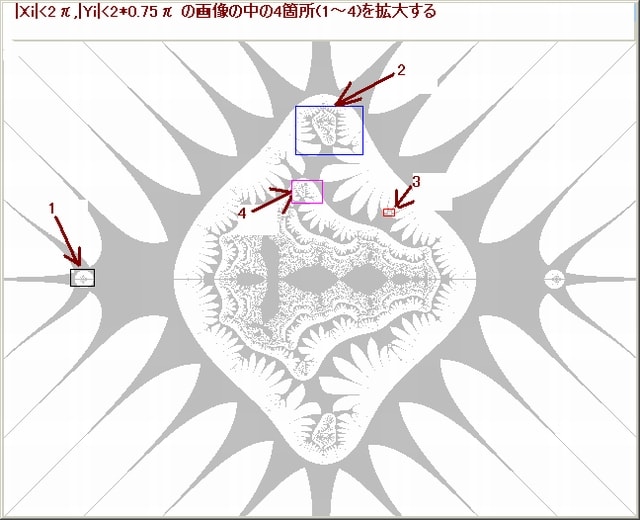
上の画像の中を下図に示した 4 箇所(1~4)を拡大する。


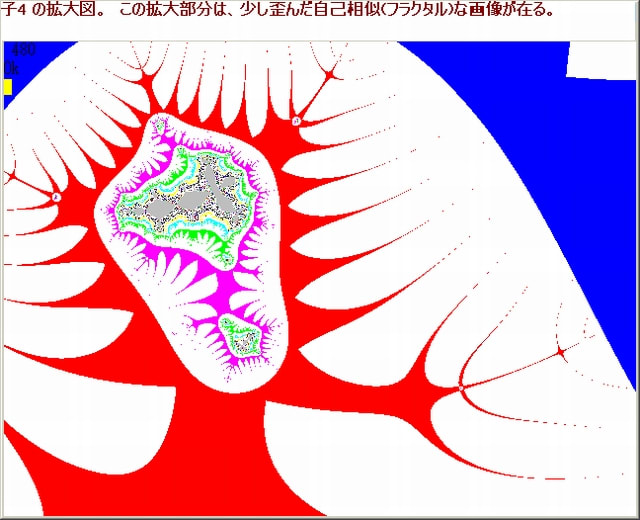
以下の画像は、上の 4 箇所の拡大画像である。これらの画像には奇妙な「腕」のような形をした図形が、ら腺階段状に1点へと収束しています。その様子は互いに相似な形をしている。




上図の 3 の画像の中の一部を更に拡大してみる。下図は、その拡大部分(1~3)を示す。


下図は上図の 3 箇所の拡大画像である。これらの画像には、上図と相似な図形であることが分かる。
つまり、Z^2*sinZ+0.46画像は自己相似(フラクタル)な画像となっています。
このブログの画像で常に現れる画像構造になっている。画像作成のプログラムが自己回帰になっているのですから、それが画像では自己相似(フラクタル)な構造として反映されているのである。



1. 複素関数:Z^2*sinZ+0.46。
2. N-loop脱出条件:Q=1/(log|X|log|Y|),(|Q|>10 or |Q|<0.1)
3. pset条件:|X|<10 or |Y|<10
4. 色設定:N-loop貫通時はC=15。N-loop脱出時は其の時のNをNoとすると C=No mod 16,C=7→8
5. Nmax=50

上の画像の中を下図に示した 4 箇所(1~4)を拡大する。


以下の画像は、上の 4 箇所の拡大画像である。これらの画像には奇妙な「腕」のような形をした図形が、ら腺階段状に1点へと収束しています。その様子は互いに相似な形をしている。




上図の 3 の画像の中の一部を更に拡大してみる。下図は、その拡大部分(1~3)を示す。


下図は上図の 3 箇所の拡大画像である。これらの画像には、上図と相似な図形であることが分かる。
つまり、Z^2*sinZ+0.46画像は自己相似(フラクタル)な画像となっています。
このブログの画像で常に現れる画像構造になっている。画像作成のプログラムが自己回帰になっているのですから、それが画像では自己相似(フラクタル)な構造として反映されているのである。