どもども。
今回からは今年の京大の入試問題(理系数学)を取り扱っていきます
誘導のない問題が幾つかあります。それゆえ手をつけにくいかもしれません。
幅広い発想力が試されそうです。
特に第6問はなかなか面白い問題だと思いました


今回は第1問(1)をやっていきます。
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon1.html
数IIIの微積分の問題です
分数ベキとか含んでるので扱いが面倒そうです。
eの定義式に関係してくるパターンかと思ったらそうでもないようです。
aが1より大きいか小さいか,あるいは1か,で場合分けが必要です。
0<a<1 のときは 0<a^n<1
1<a のときは a^n>1
が成り立つので,この不等式を使って (1+a^n)^(1/n) の評価式が簡単に得られます。
あとはハサミウチでやっつけてしまいましょう

指数の 1/n が鬱陶しい,なんとかならないか!
という人は対数をとって考えるのもいいかもしれません。
b_n=log(1+a^n)^(1/n)={log(1+a^n)}/n
とおいてb_nの極限を考察してみましょう。それを経由して答えを求めます。

この解法に関しては1つ注意を挙げておきます。
指数の極限を求めて最後はeの肩にそれを乗せて答えを求めていますが
これは関数 f(x)=e^x が連続関数だから正しいのだということを
気に留めておくと良いと思います。
無条件では lim f(a_n) と f(lim a_n) は等しくありません
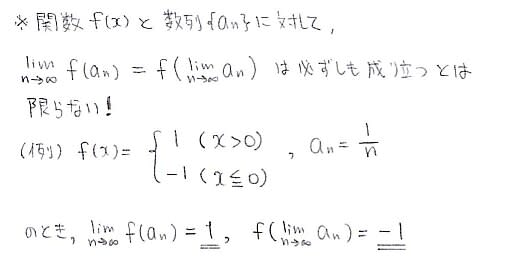
後半のa>1の場合ですが,x>0で連続な関数 f(x)={log(1+a^x)}/x の
x→∞の極限に置き換えれば∞/∞型の不定形になっているのでロピタルの定理なんかも使えます。
試験場ではロピタルの定理を使うのは躊躇われますが,ここは試験場ではないので
気にせず使っちゃいます。

ちなみに実数上で定義された関数f(x)に対して数列{f(n)}が考えられますが,
lim_{n→∞} f(n)=β であったとしても,lim_{x→∞} f(x)=β であるとは限りません。
さて,最後にもう1つ解法を挙げて終わりたいと思います。
…といっても,これは既に上の解法で答えの値を知っているから作れる解法ではあるんですが
数列{x_n}が極限αを持つことを証明する手段の1つに
lim_{n→∞}(x_n-α)=0 を証明するというものがあります。
コイツをやってみようと思います。
極限の値が1とaであるということが何らかの直感でピンときた場合
以下で挙げる手法が使えます。
それを説明するためにまず次の因数分解をみてみましょう。
x^n-1=(x-1){x^(n-1)+x^(n-2)+…+x+1}
これは等比数列の和の公式を式変形すれば直ちに得られますね。
n=2 のときの x^2-1=(x-1)(x+1) の式はあまりにもお馴染み過ぎるわけですが
ルートがらみの式の極限を求める時にしばしば分母か分子を有理化するとうまくいく,
ということがありますね
そのときによく使うのが x^2-1=(x-1)(x+1) の式だったわけです。
今回の問題は 1/n という分数ベキが出てきますが,
よくよく考えるとこれはn乗根なんですよね。
n乗根がらみの式を有理化して考えるという発想を使ってみましょう

この式を利用してみます。

有理化したときになんか上手くいきそーな値を探そう~
という観点から模索すれば直感的に1とaという値を見つけ出せるかもしれないですね。
ではでは次回は(2)をやっていきます
今回からは今年の京大の入試問題(理系数学)を取り扱っていきます

誘導のない問題が幾つかあります。それゆえ手をつけにくいかもしれません。
幅広い発想力が試されそうです。
特に第6問はなかなか面白い問題だと思いました



今回は第1問(1)をやっていきます。
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon1.html
数IIIの微積分の問題です

分数ベキとか含んでるので扱いが面倒そうです。
eの定義式に関係してくるパターンかと思ったらそうでもないようです。
aが1より大きいか小さいか,あるいは1か,で場合分けが必要です。
0<a<1 のときは 0<a^n<1
1<a のときは a^n>1
が成り立つので,この不等式を使って (1+a^n)^(1/n) の評価式が簡単に得られます。
あとはハサミウチでやっつけてしまいましょう


指数の 1/n が鬱陶しい,なんとかならないか!

という人は対数をとって考えるのもいいかもしれません。
b_n=log(1+a^n)^(1/n)={log(1+a^n)}/n
とおいてb_nの極限を考察してみましょう。それを経由して答えを求めます。

この解法に関しては1つ注意を挙げておきます。
指数の極限を求めて最後はeの肩にそれを乗せて答えを求めていますが
これは関数 f(x)=e^x が連続関数だから正しいのだということを
気に留めておくと良いと思います。
無条件では lim f(a_n) と f(lim a_n) は等しくありません

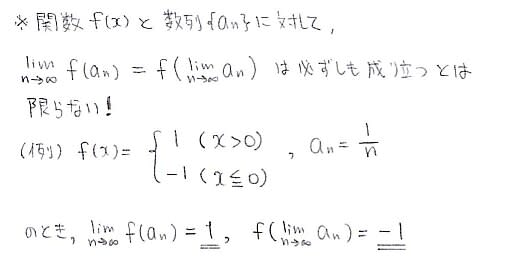
後半のa>1の場合ですが,x>0で連続な関数 f(x)={log(1+a^x)}/x の
x→∞の極限に置き換えれば∞/∞型の不定形になっているのでロピタルの定理なんかも使えます。
試験場ではロピタルの定理を使うのは躊躇われますが,ここは試験場ではないので
気にせず使っちゃいます。

ちなみに実数上で定義された関数f(x)に対して数列{f(n)}が考えられますが,
lim_{n→∞} f(n)=β であったとしても,lim_{x→∞} f(x)=β であるとは限りません。
さて,最後にもう1つ解法を挙げて終わりたいと思います。
…といっても,これは既に上の解法で答えの値を知っているから作れる解法ではあるんですが

数列{x_n}が極限αを持つことを証明する手段の1つに
lim_{n→∞}(x_n-α)=0 を証明するというものがあります。
コイツをやってみようと思います。
極限の値が1とaであるということが何らかの直感でピンときた場合
以下で挙げる手法が使えます。
それを説明するためにまず次の因数分解をみてみましょう。
x^n-1=(x-1){x^(n-1)+x^(n-2)+…+x+1}
これは等比数列の和の公式を式変形すれば直ちに得られますね。
n=2 のときの x^2-1=(x-1)(x+1) の式はあまりにもお馴染み過ぎるわけですが
ルートがらみの式の極限を求める時にしばしば分母か分子を有理化するとうまくいく,
ということがありますね

そのときによく使うのが x^2-1=(x-1)(x+1) の式だったわけです。
今回の問題は 1/n という分数ベキが出てきますが,
よくよく考えるとこれはn乗根なんですよね。
n乗根がらみの式を有理化して考えるという発想を使ってみましょう


この式を利用してみます。

有理化したときになんか上手くいきそーな値を探そう~
という観点から模索すれば直感的に1とaという値を見つけ出せるかもしれないですね。
ではでは次回は(2)をやっていきます
















※コメント投稿者のブログIDはブログ作成者のみに通知されます