僅か20歳のガロアは遺書の中の第1論文の序章で、”ある群が置換SとTを含めばその群は必ず置換STを含む”と「置換の定義」を簡単に述べてる。確かに、置換が群の定義である”結合法則と単位置換と逆置換S⁻¹を満たす”のは明らかで、”演算にて閉じてる”というだけで群の定義を保証した。
一方で、群の定義とは上の””内の4つの条件を満たす必要がある。受験生を除く多くの中高生は、これを見て”群論はアカン”となるだろう。
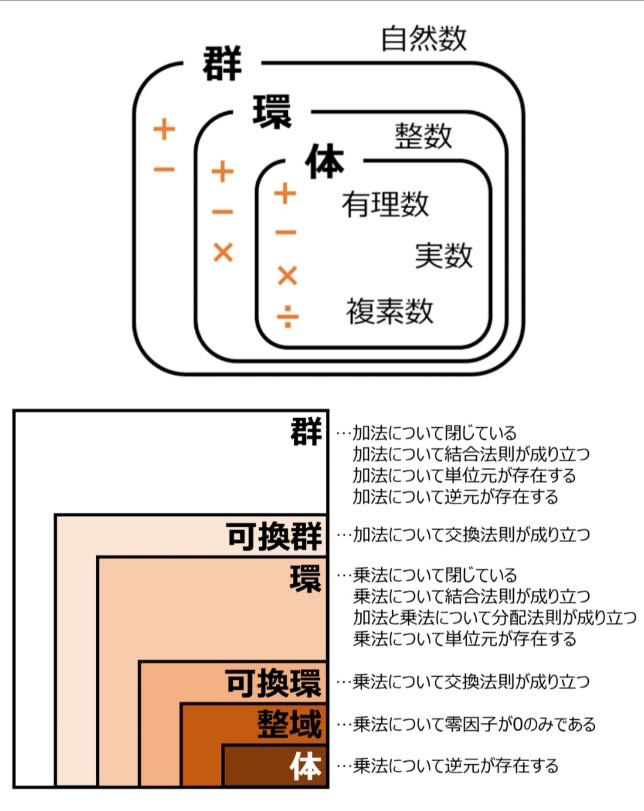
確かに、文献やサイトによって群と環と体の定義の表記は微妙に異なる(上図下参照)。
そういう私も、実は群の定義はその抽象性の高さもあり、非常に苦手で、あえて「群と環と体」というテーマで記事を書いた事があった。
勿論、書いてる事自体は間違ってはいないが、”計算の上を行く”ガロアの言葉に比べれば、まるで原始人かサルが書いてる様な次元にも思える。
そこで原点に立ち返り、もう一度、”群と環と体”をテーマにする。
解の置換がもたらしたガロア群
ガロアは、”ある群が置換SとTを含めば、その群は必ず置換STを含む”とのシンプルな条件だけで”置換が群を成す”事を述べている。つまり、僅か1つの条件だけで群の本質を見抜いてたのだ。
「代数に惹かれた数学者たち」(Jダービーシャー著)に従えば、元々群論とは置換の言葉を意味していた。ガロアによって大きな変革ををもたした方程式論だが、ジョルダンにより置換論としてガロアの死後約40年に発表された。
若干20歳にも満たないガロアは、与えられた方程式に対し、解の置換を考える事で方程式の可解性を見出す。
例えば、5次方程式のガロア群は5つの根の置換全てからなる群で解の対称性を表すが、群の構造が複雑すぎて対称性が高くなり、解の対称性を崩せない。が故にガロアは、方程式はベキ根で解けないので”5次方程式のガロア群は可解群ではない”と結論づけた。
一方で、ルフィニとアーベルは解の置換に注目し、ある置換に対しては対称だが別の置換では変更される事に気付いた。そこで、係数の体を広げて”解の体”にしたいが、一般の5次以上の方程式ではそんな拡大体が作れない事を示した。因みに、当時は”順列”と呼ばれてた置換を使い、5次方程式の非可解性を最初に証明したのはルフィニだが、ルフィニの証明は複雑すぎて、正否の判断が困難だったとされる。
アーベルは、ルフィニの不足を補い、背理法とコーシーの置換の定理を使い、5次方程式の非可解性を直接的に証明した(1824,26年)が、更に深い考察を与え、ガウスが発見した”xⁿ−1=0が可解である”という非可解性の例外を一般化した(1828年)。つまり、可解性と可換性(巡回的対称性)を結びつけ、”アーベル方程式が可解である”所までは辿り着いたが、そこで命が尽きた。
つまり、係数体にべき根を加えて拡大する手法は天才アーベルも気付いていた。だがガロアは、この拡大体をガロア群に置き換えて、群の構造を調べたのだ。
但し、こうしたアーベルの代数方程式論に関しては、別途テーマにしたいと思う。
500年先を行くとされるアーベルとガロアの2人の天才は、”観念で数学を捉えた”史上初めての数学者だと感心する。特に”計算の上を飛ぶ”ガロアのアイデアは、今も世界中から愛され、継承されている。
そこで難しい数学の話はヤメにして、仮にガロアが長生きし、大人しくパリの教育大学に通い、学校の先生になってたら、群と環と体をどんな風に教えるのであろうか。
上述した様に、代数学の教科書では”結合法則と単位元と逆元と二項演算”と、4つの条件を持ち出して群を定義し、環を通り越し(群よりも条件のキツい)体を説明する。
この群と体は、19世紀初頭に発見された2つの数学的名称だが、群の方が体よりも単純で柔軟である分、数学者にとっては取り組み甲斐があった。
ただ、群と環と体はセットにして理解すれば、怖いものなしである。
再び、群と環と体とは?
そこで今日は、”一目で分かる群と環と体”というテーマで話を進めたい。
群と環と体を一言で説明すれば”数の概念を一般化した”ものとも言える。但し、”一般化”とは物事の本質だけを切り取る事で、つまり、数を”群れ”で捉え、その本質を見抜く事である。
因みに、自然数では引き算ができない場合がある。そこで整数に拡張し、その整数も割り算ができない場合があり、有理数に拡張するが、その有理数もべき根が取れない場合があり、無理数が生まれ、2つを統合して実数とした。だが、実数では方程式の解がない場合があり、虚数が生まれ、実数と虚数を複素数(平面)としてまとめた。
こうして数の概念は拡張されていくが、こうした数の概念を一般化出来ないものか?と当時の数学者らは考えた。つまり群論とは、そんな状況から生まれた概念でもある。
と言えば、小難しい話だと思われそうだが、ガロア的に群を表現すれば至極単純になる。
そこで一旦”結合法則と単位元と逆元と二項演算”という専門用語を頭の中から外してもらいたい。
まずガロア理論には、群と体という代数的構造が登場するが、その中間に”環”という構造が存在する。
そこで、ガロア風に言えば、”群とは加算と減算の二則(加減)で閉じ、体は四則演算(加減乗除)で、環は加減乗の三則のみで閉じた集合”と二項演算のみで定義する事が出来る。
つまり、”群(ニ則)⊃環(三則)⊃体(四則)”と単純に覚えとけば、まずは間違いない(上図参照)。
因みに、整数・有理数・実数・複素数は加算に関して交換則が成り立ち、可換群(加法群)となる。一方で、”0を除く”という条件では、実数や有理数や複素数は”積に関しては”群となる。これは、0には積に関する逆元1がないからだ。
しかし、自然数は減算で閉じないので群にはなりえない。また、整数は加減乗の三則で閉じるので環となる。更に、整数は乗算にて(交換則が成立し)可換環となるが、同じ理由で有理数・実数・複素数も可換環となる。
一方で、整数だけは体にはなり得ない。当然だが、四則のうち除算を満たさないからだ。
故に体を満たすのは、自然数Nと整数Zを除いた有理数Q・実数R・複素数Cのみとなる(上図参照)。
群と置換の密な関係
この様に、”結合法則と単位元と逆元”という3つ専門用語を切り離すだけで、群と環と体の理解はずっと身近に、そして楽になる。
また、こうした群の概念は置換や数以外にも、写像や多項式や関数などにも使える。
例えば、写像は合成を演算とすれば群をなし、対称群と見れば、その元は(ものを置き換える操作である)置換を成す。
また、多項式も整数同様に可換環をなし、”ユークリッドの互除法”が使え、ガロアは”最大公約式は有理的である”とみなし、”ラグランジュの定理”(単拡大定理)に結びつけ、方程式論の起点にした。
今のように群の定義が明確でなかった当時においては、群といえど置換を調べるツールに過ぎなかった。少なくとも、今の様に複雑に絡み合った定義で縛り上げられたものではなかった筈だ。少なくともガロアは計算の上を飛んだのだから・・・
一方で、ガロア理論の元となった”体の概念”では、Q,R,C以外の体と言えば、有限体と拡大体の2つしかない。
つまり、Q,R,Cは全て無限に多くの元があるが、有限体とは有限個の元を持つ体という集合だ。勿論、5次方程式の係数を元として集めたものは係数体(基礎体)と呼ばれ、有限体となる。
事実、前出のルフィニは、5次方程式の解の置換を120個(=5!)の元からなる5次の対称群とみなし、1つ1つ調べ上げた。それでもアーベルがいなかったら、彼の証明は不完全なままであった筈だ。
一方で拡大体だが、係数体にべき根を次々と添加していった拡大体の事を言う。こうして拡大体を大きく膨らませる事で解けなかった方程式が解ける様になる。
この拡大体は元の係数体Q上のベクトル空間となるが、べき根を加える事で拡大体の次元は増え、ベクトルの次数(基底)も増える。
ガロアはこうして広げた拡大体を”解の体”とみなし、係数体と解の体の関係を探り、方程式の解の置換で得られたガロア群と1対1で結びつけた。これこそがガロア群による代数方程式論だが、彼が生み出したガロア理論の理想はもっと高みにあった。
”計算の上を飛ぶ”という次元よりもずっと高みにあった筈だ。事実、モジュラ関数や超楕円関数論に飛躍させたガロア理論を(泣く子も黙る)ヒルベルトを師に持つ高木貞治氏は”夢のようだ”と絶賛し、感服した。
事実、ガロアの代数方程式論は約40年後にジョルダンが判読し、「置換論」を成した。だが、アーベルを引き継いだガロアの積分論は25年後にリーマンに発見されて後、初めて記録に上がったのだ。
最後に
今では、”群”で検索すれば、ありとあらゆるきめ細かい定義でサイトは埋め尽くされている。群とは(今更だが)厳密には、(結合則のみを満たす)半群・(結合則と単位元を満たす)モノイド・(結合則と単位元と逆元を満たす)群・(更に交換則を満たす)可換群とに区別され、故にそれらに応じた様々な約束事も例外も存在する。
こうした、後付けされた細かい形式を述べればキリがないが、もうこの時点でアウトという人も多いだろう。私もその1人であり、そこまでして数学に人生を捧げたいとも思わない。
それに、それら抽象的で複雑でややこしい理論はガロアの本意ではない筈だ。
冒頭でも述べたが、群論とは置換の言葉を意味するに過ぎないし、ガロアはそれを代数方程式の解の判定に利用しただけである。事実、前出の高木氏はガロアの方程式論(第一論文)を”長足の進歩”と評価はしてるが、”夢のようだ”と絶賛した”積分法”ほどでもない。
つまり、ガロア理論の本質は第2論文の楕円関数論や第3論文の積分法(超楕円関数論)にあったのだから・・・
一方で群の歴史を見れば、その概念が数学史上初めて明確に表出したのは、ガロアによる根の置換群を用いた代数方程式の研究である。
18世紀後半にラグランジュにより方程式の解法が根の置換と関係してる事が発見され、群の研究は進んではいた。故に、群の歴史を語る時に、”ラグランジュの定理”が外せないのもその為である。
19世紀に入り、(前述の様に)ルフィニやアーベルによって、係数体にべき婚を加え拡大し、5次以上の方程式には代数的な解法が存在しない事が示され、代数方程式の未解決問題に決着がついたかに思えた。
一方でガロアは更に歩を進め、べき根で解けるか否かを(方程式の)ガロア群の可解性に帰着した。
こうした群を用いたガロアの方程式論は、今ではガロア理論と呼ばれ、5次以上の代数方程式の非可解性は”交代群が単純(正規部分群を持たない群)である”事で説明がつく。
事実、ガロア群が正規部分群に分解できれば可解となる。
一方で、有限群の理論は市場調査や宇宙論に至る数々の実用分野に用途が見つかっている。また群の分類の研究も進み、色んな位数の群が発見された。実際に、5次方程式のガロア群で言えば、位数120の対称群S₅や位数60の交代群A₅や位数5の巡回群C₅の他に位数20のフロベニウス群F₅や位数10の2面体群D₅の5種類ある事が知られている。故に、既約な5次方程式のガロア群は位数120の対称群S₅に分類される。
結局は、ややこしい抽象論で終始したが、群を数の”群れ”と捉え、その定義を”群(ニ則)⊃環(三則)⊃体(四則)”と演算のみで理解すれば、頭を悩ます事はない筈だ(と思うのだが)。
数学は本質を見抜く学問である。記号のお遊びでも関数等式の羅列でも、更に言えば、定理や定義や命題の牢獄でもない。
が悲しいかな、私が書いてるのは(所詮は)抽象論の羅列に過ぎないのだろう。










x⁵−ax⁴+bx³−cx²+dx−e=0と書き、その解xをべき根と係数を含む形の代数式で表す。
これはオイラーが予想した解の一般形に近いが、5次方程式の解をこの様な代数式であるとし、これが矛盾する事を示して、5次方程式の非可解性を証明した。
1854年の論文では、このxの代数式の詳細な証明を省略してたが、勘のいい人はある程度はこの代数式の形を予測できるかもしれない。
つまり、べき根と係数が方程式の解の有理式となる訳だが、ルフィニはこの証明を飛ばし、仮定だけで先に進めたとされる。
アーベルの天才ぶりはこういう所にあり、解の有理式を求める際に、この代数式を使って解を置換するのだが、コーシーの置換の法則より、矛盾が発生して解の公式が作れない。
以上から、アーベルの天才が当時の数学界において如何に突出していたか?
ガロアは更にアーベルの天才の核心を掴んでいた。ガロアの天才もまた脅威である。
言われる通り
アーベルによる代数的解の一般形(代数式)ですが、係数から作られる有理式全体にべき根を添加する操作を繰り返した結果得られるもので、この厳密な証明を1824年の論文では省略してました。
だた、このアイデアこそがアーベルの天才であり、彼の純朴で直線的な性格を表してます。
例えば、2次方程式でみれば、その解は(a,b,cの有理式)+√(a,b,cの有理式)の形の代数式となりますから、5次方程式はこの延長上にあると直感で閃いたんですかね。
これ以上書くとネタバレになりますが、アーベルの天才的アイデアには只々脱帽です。
何時もコメントとても勉強になります。
”(a,b,cの有理式)+√(a,b,cの有理式)”と書きましたが、正確には”(aの有理式)+√(a,bの有理式)”でした。
悪しからずです。
相手にしたくはないのですが
①は35で
②は15+3=18で