開平と開立（第12回）：237,169の算盤による開平（倍根法６）

「開平はん」に237,169を置いたところ

拡大

[English]

前回に続き、算盤での開平の手順を解説する。今回も倍根法で、根が３桁、過大根が生じ途中で根を還元する必要がでてくる。理論編も参考にしていただきたい。

開平（平方根）：倍根法(2商法)、倍根法別法、半九九法、半九九法別法、乗減法、定数法(折衷法) 、過大数開平、省略開平など


算盤による237,169の2乗根の解法（答は487）

第１群の数とは平方根を求める数を２桁ずつ区切り、いちばん大きい（いちばん左）の２桁のことである。群の数が根の桁数となる。

237169 -> (23|71|69) : 23が第１群の数、根の桁数は3


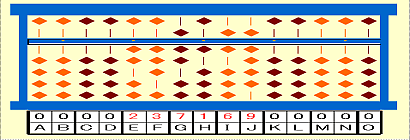
手順１：237169を置く。第1群は23。


手順２：23以下の平方数は16=4x4。4を初根としてDに立てる。


手順３：4の平方を第1群の23から引く。23-16=07となる。： -a^2


手順４：初根4の2倍8をAに置き、倍根とする。77に注目する。


手順５：77を倍根8で割る。商9を得て、割止める。次根9をEに置く。


手順６：FGの77から倍根8と次根9の積を引く。77-8x9=05をFGに置く。


手順７：9の平方=81を第2群の51から引けないので9は過大根だとわかる。よって次根9から1を引き8をEに置く。そして倍根8を還元して05+08=13をFGに置く。


手順８：次根8とFGHの131に注目する。


手順９：次根8の平方=64をFGHの131から引く。131-64=67をGHに置く。


手順１０：倍根80と次根8に注目する。


手順１１：次根8の2倍(=16)を倍根80に加える。2x8+80=96をABに置く。


手順１２：GHIの676を倍根96で割る。


手順１３：商7を得て、割止め、この商を第3根とする。第3根の7をFに置き、余り676-96x7=004をGHIに置く。


手順１４：第3根7と第3群IJの49に注目する。


手順１５：第3根7の平方=49を第3群の49から引く。49-49=00をIJに置く。


手順１６：根は487と求まる。


最終状態： 答 487

珠の状態推移を表にすると次のようになる。（クリックで拡大）



第１３回も引き続き倍根法による開平を行う。


関連記事：

ファインマン v.s. 算盤の達人： ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb

目次：算盤による平方根、立方根の計算（開平、開立）
http://blog.goo.ne.jp/ktonegaw/e/bb0449f357398a2c24026f33af7f70ee


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。
　　

とね日記は長年放置されている科学ブログランキングの不正クリックに対し、次のランキングサイトには適切な運営を期待します。
「FC2自然科学ブログランキング」：不正の例１ 例２
「にほんブログ村、科学ブログランキング」：New-不正の例１
（不正クリックブログの見分け方）