
「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ: 中山茂」(感想記事)
内容紹介:
IBMから提供される無料の量子計算プラットフォームを体験する!大学での講義を想定した豊富な例題、演習、実験で理解を深める。16の量子実験を通して、量子アルゴリズムを学び、量子シミュレーションで実行する。
2016年10月10日刊行、331ページ。
著者について:
中山茂(なかやましげる)
京都生まれ。京都大学大学院工学研究科博士課程修了後、上智大学、英国Reading大学、京都工芸繊維大学、兵庫教育大学、英国Oxford大学、鹿児島大学を経て、2014年に定年退職。京都大学工学博士。
理数系書籍のレビュー記事は本書で329冊目。
IBM Quantum Experience(入口)
http://www.research.ibm.com/quantum/
前回の「クラウド量子計算入門: 中山茂:(2) ブログ記事の方針変更」という記事で『「Real Quantum Processor」を選択すると、配置できる測定アイコンはひとつだけなので、量子ビット毎に複数の測定アイコンを置くことができない。またブロッホ球測定のアイコンは現在の仕様では無くなってしまっている。』と書いたのだが、まったく違うことがわかったので取り急ぎ訂正記事として投稿させていただこう。
まず、測定アイコンはずらした形に置けば複数配置して実験することができることがわかった。この図でQuantum Circuitの中で斜めに3つ配置したピンク色のアイコンのことである。

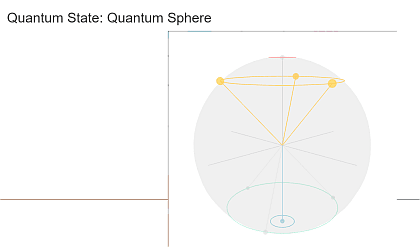
またブロッホ球測定のアイコンがComposer上に配置できないというのは本当だが、現在の仕様で(ブロッホ球ではなく)量子球が測定結果のページに自動的に表示されるようになっている。ただし、本書が書かれていたときの表示方法とは違うので、注意が必要だ。たとえばこの画像のように3つの量子ビットが1つの量子球に表示されるのが現在の仕様だ。
ブロッホ球と量子球の違いはこのページをお読みいただきたい。
上にあげた2つのスクリーンショットは本書の268ページで説明されている「GHZ状態のZZZ測定」という実験を行った結果だ。実験結果はユーザー登録していなくても「このリンク」を開いて「Show Results」というボタンをクリックするとご確認いただける。
これは多粒子(この場合は3粒子)のもつれ状態である「GHZ状態」を用いて量子非局所性状態を証明するための実験だ。2粒子系の「ベル状態」よりも3粒子系の「GHZ状態」を用いたほうが局所実在性の破れが強く出て、ベル状態の局所実在性の確率論的な破れよりも、GHZ状態の局所実在性のほうが決定論的な破れがあるとされている。
この実験でアインシュタインが「不可解な遠隔作用」、「EPRパラドックス」として忌み嫌った状況が量子コンピュータ内に再現できたことになる。
ということで、本書に解説されているすべての実験は現在公開されている量子コンピュータで実験可能であることがわかった。けれども、章ごとにすべて実験して紹介すると1年くらいかかってしまう。だから、いくつかめぼしい実験を紹介をするにとどめ、本全体の感想記事として後日書かせていただくことにしたい。
著者の中山先生は次の本も2年前にお書きになっている。目次を見ると本書の理論的側面を学べる本だということがわかる。合わせてお読みになるとよいだろう。Kindle版は固定レイアウトなのでご注意。
「量子アルゴリズム:中山茂」(Kindle版)(目次)

量子コンピュータ関連の本: Amazonで検索
関連記事:
発売情報: クラウド量子計算入門: 中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d
クラウド量子計算入門: 中山茂:(4) 全体の感想
http://blog.goo.ne.jp/ktonegaw/e/ad7dfbad69e1e196848be123e3f4ea3f
量子コンピュータ入門:宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320
ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79
量子コンピュータ、量子アルゴリズムを学びたい高校生のために
http://blog.goo.ne.jp/ktonegaw/e/1b2940b648bda682aa27192eb8261972
発売情報:量子プログラミングの基礎: イン・ミンシェン
http://blog.goo.ne.jp/ktonegaw/e/27e4d9a10982d4d69c0029fc4c801708
関連ページ:
IBMの量子コンピュータを使ってみた
http://kadora.hatenablog.com/entry/2016/09/10/230116
従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー
http://gigazine.net/news/20151210-quantum-computers-explained/
わかりやすい量子コンピュータ
http://matome.naver.jp/odai/2133630808407668301
「ITエンジニアのための量子コンピュータ入門」連載一覧
http://codezine.jp/article/corner/629
量子力学の反常識が創りだす量子コンピューティングの世界
~量子コンピュータの頭脳としての量子アルゴリズム~
http://www.kyoto-su.ac.jp/project/st/st14_03.html
米メリーランド大学、世界初となる「汎用計算可能量子コンピュータ」モジュールを開発
http://pc.watch.impress.co.jp/docs/news/1014034.html
関連動画:
量子論、量子テレポーテーション、量子コンピュータ
量子の制御とコンピュータ(量子コンピュータの原理の概要説明)
量子コンピュータ授業 #1(15回の講義。本書で解説される量子ゲート、量子アルゴリズムのほとんどを学ぶことができる。)
15回の講義内容

ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。







「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ: 中山茂」(感想記事)

第1章 はじめてのIBMの5量子ビット実験
1.1 IBMの量子シミュレーションと量子コンピュータ実験
1.2 クラウド量子計算に期待されること
1.3 クラウド量子計算への歩み
1.4 はじめてのIBMのクラウド量子計算
1.5 はじめてのIBMの量子シミュレータ
1.6 はじめてのIBMの量子コンピュータ
第2章 パウリゲートの量子実験
2.1 パウリゲートとは
2.2 恒等ゲートとパウリゲートを使った量子シミュレータ実験
第3章 アダマールゲートの量子実験
3.1 アダマール変換とは
3.2 アダマール演算による量子シミュレータ実験
第4章 位相シフトゲートの量子実験
4.1 位相シフト演算とは
4.2 T深度による量子実験
第5章 制御NOTゲートの量子実験
5.1 制御NOTゲートと重ね合わせ状態
5.2 制御NOTゲートによるもつれ状態生成
5.3 制御NOTゲートにおけるパウリ演算子
5.4 制御NOTゲートによる交換ゲート
5.5 制御Uゲートの生成
第6章 トフォリゲートの量子実験
6.1 3量子ビットのもつれ状態
6.2 トフォリゲートの量子実験
6.3 フレッドキンゲートの量子実験
第7章 ドイチ・ジョザ問題の量子実験
7.1 ドイチ問題の量子実験
7.2 ドイチ・ジョザ問題の量子実験
第8章 ベルンシュタイン・ヴァジラニ問題の量子実験
8.1 関数f(x)=x・aの定数aを求めるベルンシュタイン・ヴァジラニ問題
8.2 n=1のベルンシュタイン・ヴァジラニ問題
8.3 n=2のベルンシュタイン・ヴァジラニ問題
8.4 n=3のベルンシュタイン・ヴァジラニ問題
第9章 サイモン問題の量子実験
9.1 サイモン問題とは
9.2 n=2のサイモン問題の量子実験
第10章 量子フーリエ変換の量子実験
10.1 量子フーリエ変換の定義
10.2 量子フーリエ変換に必要な制御Sゲートの作成
10.3 量子フーリエ変換ゲートの実装
10.4 逆量子フーリエ変換ゲート
10.5 量子フーリエ変換によるシフト不変性
第11章 位相・固有値・位数推定問題の量子実験
11.1 位相推定問題の量子実験
11.2 ユニタリ変換の固有値推定アルゴリズムの量子実験
11.3 位数発見アルゴリズムの量子実験
第12章 ショアの素因数分解問題の量子実験
12.1 因数分解とユークリッドの互除法
12.2 ショアの素因数分解アルゴリズム
12.3 ショアの素因数分解のための量子回路
第13章 グローバーの探索問題の量子実験
13.1 グローバーの探索問題とは
13.2 グローバーの振幅増幅手法の量子回路
第14章 量子非局所性の量子実験
14.1 量子非局所性とCHSH不等式
14.2 GHZ状態の量子非局所性実験
第15章 量子通信の量子実験
15.1 量子高密度符号
15.2 量子転送
第16章 量子エラーとスタビライザー測定
16.1 量子エラーとシンドローム診断
16.2 ビットパリティ識別
16.3 符号パリティ識別
第17章 量子誤り訂正の量子実験
17.1 量子誤り訂正のための符号化と複合化
17.2 量子誤り訂正ゲート
内容紹介:
IBMから提供される無料の量子計算プラットフォームを体験する!大学での講義を想定した豊富な例題、演習、実験で理解を深める。16の量子実験を通して、量子アルゴリズムを学び、量子シミュレーションで実行する。
2016年10月10日刊行、331ページ。
著者について:
中山茂(なかやましげる)
京都生まれ。京都大学大学院工学研究科博士課程修了後、上智大学、英国Reading大学、京都工芸繊維大学、兵庫教育大学、英国Oxford大学、鹿児島大学を経て、2014年に定年退職。京都大学工学博士。
理数系書籍のレビュー記事は本書で329冊目。
IBM Quantum Experience(入口)
http://www.research.ibm.com/quantum/
前回の「クラウド量子計算入門: 中山茂:(2) ブログ記事の方針変更」という記事で『「Real Quantum Processor」を選択すると、配置できる測定アイコンはひとつだけなので、量子ビット毎に複数の測定アイコンを置くことができない。またブロッホ球測定のアイコンは現在の仕様では無くなってしまっている。』と書いたのだが、まったく違うことがわかったので取り急ぎ訂正記事として投稿させていただこう。
まず、測定アイコンはずらした形に置けば複数配置して実験することができることがわかった。この図でQuantum Circuitの中で斜めに3つ配置したピンク色のアイコンのことである。

またブロッホ球測定のアイコンがComposer上に配置できないというのは本当だが、現在の仕様で(ブロッホ球ではなく)量子球が測定結果のページに自動的に表示されるようになっている。ただし、本書が書かれていたときの表示方法とは違うので、注意が必要だ。たとえばこの画像のように3つの量子ビットが1つの量子球に表示されるのが現在の仕様だ。

ブロッホ球と量子球の違いはこのページをお読みいただきたい。
上にあげた2つのスクリーンショットは本書の268ページで説明されている「GHZ状態のZZZ測定」という実験を行った結果だ。実験結果はユーザー登録していなくても「このリンク」を開いて「Show Results」というボタンをクリックするとご確認いただける。
これは多粒子(この場合は3粒子)のもつれ状態である「GHZ状態」を用いて量子非局所性状態を証明するための実験だ。2粒子系の「ベル状態」よりも3粒子系の「GHZ状態」を用いたほうが局所実在性の破れが強く出て、ベル状態の局所実在性の確率論的な破れよりも、GHZ状態の局所実在性のほうが決定論的な破れがあるとされている。
この実験でアインシュタインが「不可解な遠隔作用」、「EPRパラドックス」として忌み嫌った状況が量子コンピュータ内に再現できたことになる。
ということで、本書に解説されているすべての実験は現在公開されている量子コンピュータで実験可能であることがわかった。けれども、章ごとにすべて実験して紹介すると1年くらいかかってしまう。だから、いくつかめぼしい実験を紹介をするにとどめ、本全体の感想記事として後日書かせていただくことにしたい。
著者の中山先生は次の本も2年前にお書きになっている。目次を見ると本書の理論的側面を学べる本だということがわかる。合わせてお読みになるとよいだろう。Kindle版は固定レイアウトなのでご注意。
「量子アルゴリズム:中山茂」(Kindle版)(目次)

量子コンピュータ関連の本: Amazonで検索
関連記事:
発売情報: クラウド量子計算入門: 中山茂
http://blog.goo.ne.jp/ktonegaw/e/d360b69100fbe723c5b9410dbf3f5f4d
クラウド量子計算入門: 中山茂:(4) 全体の感想
http://blog.goo.ne.jp/ktonegaw/e/ad7dfbad69e1e196848be123e3f4ea3f
量子コンピュータ入門:宮野健次郎、古澤明
http://blog.goo.ne.jp/ktonegaw/e/ef75709187cf4b35a12f2d9fdf73a320
ファインマン計算機科学:ファインマン, A.ヘイ, R.アレン
http://blog.goo.ne.jp/ktonegaw/e/4f7f453019fd463ed2bfdeaa7b288d79
量子コンピュータ、量子アルゴリズムを学びたい高校生のために
http://blog.goo.ne.jp/ktonegaw/e/1b2940b648bda682aa27192eb8261972
発売情報:量子プログラミングの基礎: イン・ミンシェン
http://blog.goo.ne.jp/ktonegaw/e/27e4d9a10982d4d69c0029fc4c801708
関連ページ:
IBMの量子コンピュータを使ってみた
http://kadora.hatenablog.com/entry/2016/09/10/230116
従来のPCの1億倍高速な量子コンピューターはどのような仕組みで動いて物理的限界を突破しているのかがわかるムービー
http://gigazine.net/news/20151210-quantum-computers-explained/
わかりやすい量子コンピュータ
http://matome.naver.jp/odai/2133630808407668301
「ITエンジニアのための量子コンピュータ入門」連載一覧
http://codezine.jp/article/corner/629
量子力学の反常識が創りだす量子コンピューティングの世界
~量子コンピュータの頭脳としての量子アルゴリズム~
http://www.kyoto-su.ac.jp/project/st/st14_03.html
米メリーランド大学、世界初となる「汎用計算可能量子コンピュータ」モジュールを開発
http://pc.watch.impress.co.jp/docs/news/1014034.html
関連動画:
量子論、量子テレポーテーション、量子コンピュータ
量子の制御とコンピュータ(量子コンピュータの原理の概要説明)
量子コンピュータ授業 #1(15回の講義。本書で解説される量子ゲート、量子アルゴリズムのほとんどを学ぶことができる。)
15回の講義内容

ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。




「クラウド量子計算入門―IBMの量子シミュレーションと量子コンピュータ: 中山茂」(感想記事)

第1章 はじめてのIBMの5量子ビット実験
1.1 IBMの量子シミュレーションと量子コンピュータ実験
1.2 クラウド量子計算に期待されること
1.3 クラウド量子計算への歩み
1.4 はじめてのIBMのクラウド量子計算
1.5 はじめてのIBMの量子シミュレータ
1.6 はじめてのIBMの量子コンピュータ
第2章 パウリゲートの量子実験
2.1 パウリゲートとは
2.2 恒等ゲートとパウリゲートを使った量子シミュレータ実験
第3章 アダマールゲートの量子実験
3.1 アダマール変換とは
3.2 アダマール演算による量子シミュレータ実験
第4章 位相シフトゲートの量子実験
4.1 位相シフト演算とは
4.2 T深度による量子実験
第5章 制御NOTゲートの量子実験
5.1 制御NOTゲートと重ね合わせ状態
5.2 制御NOTゲートによるもつれ状態生成
5.3 制御NOTゲートにおけるパウリ演算子
5.4 制御NOTゲートによる交換ゲート
5.5 制御Uゲートの生成
第6章 トフォリゲートの量子実験
6.1 3量子ビットのもつれ状態
6.2 トフォリゲートの量子実験
6.3 フレッドキンゲートの量子実験
第7章 ドイチ・ジョザ問題の量子実験
7.1 ドイチ問題の量子実験
7.2 ドイチ・ジョザ問題の量子実験
第8章 ベルンシュタイン・ヴァジラニ問題の量子実験
8.1 関数f(x)=x・aの定数aを求めるベルンシュタイン・ヴァジラニ問題
8.2 n=1のベルンシュタイン・ヴァジラニ問題
8.3 n=2のベルンシュタイン・ヴァジラニ問題
8.4 n=3のベルンシュタイン・ヴァジラニ問題
第9章 サイモン問題の量子実験
9.1 サイモン問題とは
9.2 n=2のサイモン問題の量子実験
第10章 量子フーリエ変換の量子実験
10.1 量子フーリエ変換の定義
10.2 量子フーリエ変換に必要な制御Sゲートの作成
10.3 量子フーリエ変換ゲートの実装
10.4 逆量子フーリエ変換ゲート
10.5 量子フーリエ変換によるシフト不変性
第11章 位相・固有値・位数推定問題の量子実験
11.1 位相推定問題の量子実験
11.2 ユニタリ変換の固有値推定アルゴリズムの量子実験
11.3 位数発見アルゴリズムの量子実験
第12章 ショアの素因数分解問題の量子実験
12.1 因数分解とユークリッドの互除法
12.2 ショアの素因数分解アルゴリズム
12.3 ショアの素因数分解のための量子回路
第13章 グローバーの探索問題の量子実験
13.1 グローバーの探索問題とは
13.2 グローバーの振幅増幅手法の量子回路
第14章 量子非局所性の量子実験
14.1 量子非局所性とCHSH不等式
14.2 GHZ状態の量子非局所性実験
第15章 量子通信の量子実験
15.1 量子高密度符号
15.2 量子転送
第16章 量子エラーとスタビライザー測定
16.1 量子エラーとシンドローム診断
16.2 ビットパリティ識別
16.3 符号パリティ識別
第17章 量子誤り訂正の量子実験
17.1 量子誤り訂正のための符号化と複合化
17.2 量子誤り訂正ゲート






















Q1.素粒子の世界では、未来の観測が過去に影響するという説があると聞きました。
この説はもう定説なのでしょうか?
Q2.またそれとは関係ないのですが、遠距離の電線や光ファイバを瞬時に電子や光が伝搬するのは、単に遅延時間を有しているからか、波動として伝搬するからと考えるべきなのでしょうか?
以前から疑問に感じていたことです。もし気が向いたらお応え下されば結構です。 以上
ブログをお読みいただき、ありがとうございます。ご質問いただいた2つはまさに量子力学の核心をつくところです。つまり電子や光子を波動として考えるか、粒子として考えるかということです。どちらも正しいということが量子性ということですよね。
Q1.素粒子の世界では、未来の観測が過去に影響するという説があると聞きました。
この説はもう定説なのでしょうか?
定説ですか?という質問はこの現象が正しいと科学者の多くが認めているか?というご質問ですよね?
僕の理解ではこの実験が行われ、この現象が確認されたという事実はあります。そして未来の観測が過去に影響を与えるか?ということについては半分正しく、半分正しくないということです。
つまりこれは「遅延選択実験」のことですね。光を光子(粒子)として考えれば未来の観測が過去に影響を与えたことになります。しかしこの実験は光を波動として考えれば、つまり古典的な電磁波として考えれば未来の観測が過去に影響を与えたとは考えられなくなります。(この実験は古典的な電磁波で説明可能という意味です。)次の2つの記事をお読みになるとわかると思います。量子力学の粒子性、波動性が両立していると考えるならば、どちらも正しいという結論になると思います。
遅延選択量子消去実験は本当なの?
http://www7b.biglobe.ne.jp/~kcy05t/nidcqe.html
過去は変えられる?思考実験『ホイーラーの遅延選択実験』が実際に行われた ? 量子における『観測』
http://sign.jp/df2c49f8
Q2.またそれとは関係ないのですが、遠距離の電線や光ファイバを瞬時に電子や光が伝搬するのは、単に遅延時間を有しているからか、波動として伝搬するからと考えるべきなのでしょうか?
光子の場合、波動として考えるならば電磁波の速度で伝わります。通過する物質の影響で速度に微妙な変化はありますね。真空中と水中で速度が違うから光線の屈折がおきるわけです。光ファイバの中を光が伝搬するのは電磁波の伝搬として考えるのが妥当だと思います。
電子の場合、電子を粒として考えれば量子力学の法則に従い電子はジグザグ運動をします。瞬間瞬間ごとに電子は光速で運動しますが、ジグザグ運動をするために広い範囲で考えれば遅く運動しているように見えるわけです。(ランダムウォークするからという意味です。)電線の中でもそのようなことがおきています。
電線を伝わる「電流」は電子の集合体の移動ですが、この移動速度は上記の電子のランダム運動のために「電子の速度」は毎秒数ミリメートルです。でも電子の集合体として考えると、電流は筒の中に詰めた「ところてん」のようなものですから、片方の端から押すともう一方の端からはみ出してくるようなことがおこり、瞬時(実は光速度と同じ)に伝わるように見えるのです。
波動関数としては光子の場合は電磁波、つまりマクスウェルの方程式、そして電子の場合はシュレディンガーの方程式ということになります。
電子の運動については以下の本の紹介記事の中で触れておきました。
量子波のダイナミクス:森藤正人
http://blog.goo.ne.jp/ktonegaw/e/20dea8ac600f55f0c79934c6342e8c5c
量子力学と経路積分:R.P.ファインマン、A.R.ヒッブス
http://blog.goo.ne.jp/ktonegaw/e/2b9d934a542cf04be54cbede8b16ecde
それは電線の中にもともとある自由電子による電場のことですよね?(違うかのかな?)
電線の電流は電子が電源から押されて動くのではなく、外にある電場で動かされるのですが、電場はスイッチを入れる前から存在し、スイッチは電子が動けるかどうかだけを変える物です。
電流のエネルギーは何処を動くかの答が、電線の周りに存在するポインティングベクトルなのと同様な話。
へえ、そうなのですね!教えていただき、ありがとうございます!
「ところてん方式」(電子が電源から押されることで電線の電流が流れる)は電子回路の入門書で読んで知ったものです。
オイラトライオ様
電流の流れるしくみについては間違ったことをお伝えしてしまいました。申し訳ありません。
また時々訪問します。
どういたしまして。僕もhirotaさんから教えていただき、電流の伝わり方について正しく理解できたのでよかったです。
残念ながら、現在のシミュレーターの仕様では、Bloch Measurement のアイコンが表示されないので、書籍で多用しているブロッホ球での動作確認ができず、標準基底測定でしか観察できません。この場合は、ブロッホ球ではなく、量子球での表示になってしまい、全体的な情報しか得られません。
また、|+> のベクトルの表示は、ブロッホ球と量子球では、まったく異なった方向を向いてしまいます。
本ページでお書きになっている『ブロッホ球』という用語は『量子球』ではないかと思いますが、いかがでしょうか?
本日より読み始めたばかりなので、勘違いかもしれませんが、その節はお許しください。
また、現在のバージョンでは、計算結果の Quantum State のグラフの横軸が、ソートされていない2進数になってしまっていて、読みづらいので、CSV出力して Excel でソートして眺めています。
Web 版で、横軸をソートして出力させるオプションなどがありましたら、是非、お教えください。
また、かつての、Bloch measurement と類似の機能を Web 版で使える方法などがありましたら、あわせてご教授いただけますと幸いです。
よろしくお願いいたします。
コメントいただき、ありがとうございます。
ご指摘のとおりこの記事ではブロッホ球と量子球を混同していました。記事を修正しておきました。
この本の執筆当時の仕様と変わってしまい、本書の使い勝手が悪くなったことを残念に思います。本書だけでなく、量子コンピュータの教科書ではブロッホ球で説明しているものばかりですから。
このブログ記事を書いたころより、いまでは次のページが充実してきましたので、本書とこちらを併読されるとよいでしょう。
IBM Quantum Computing で計算してみよう
https://www.ibm.com/developerworks/jp/cloud/library/cl-quantum-computing/index.html
> Web 版で、横軸をソートして出力させるオプションなどがありましたら、是非、お教えください。
調べてみました。残念ながらそのような(便利な)オプションは見つかりませんでした。
ユーザーとしては、現在の本書の改訂版がでるか、この無料実験サイトの仕様がもう少し改善されるかを待つしかありませんね。今後10~50量子ビットの量子コンピュータが無料公開されることになるかもしれませんが、初心者が学習するという意味では現在の5量子ビットくらいがちょうどよいと思います。