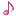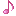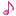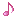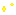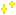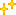Square root 164,836 using abacus (Double-root method 8)

[Set 164,836 on Mr. Square root]

Zoom

[Japanese]

We will continue from where we ended in the last article, the article shows actual solutions to calculate Square root using abacus. Today's example is simple - basic Double-root method, root is 3-digits case. There is Zero in root. Please check the Theory page for your reference.

Square root methods: Double-root method, Double-root alternative method, half-multiplication table method, half-multiplication table alternative method, multiplication-subtraction method, constant number method, etc.


Abacus steps to solve Square root of 164,836
(Answer is 406)

"1st group number" is the left most numbers in the 2-digits groups of the given number for square root calculation. Number of groups is the number of digits of the Square root.

164836 -> (16|48|36) : 16 is the 1st group number. The root digits is 3.


Step 1: Set 164836. 1st group is 16.


Step 2: Square number smaller than or equal to 16 is 16=4^2. 4 is the 1st root.


Step 3: Subtract 4^2 from the 1st group 16. 16-16=00


Step 4: Place 8 which is 2x of 1st root 4. This 8 is double root. Focus on 48.


Step 5: Cannot divide 04 by 8. Place 0 on E as 2nd root.


Step 6: Divide 483 by double root 80.


Step 7: Answer is 6 and this is 3rd root.


Step 8: Place 483-80x6=003 on GHI.


Step 9: Subtract square of 3rd root 6 from 36 on IJ.


Step 10: Place 36-6x6=00 on IJ.


Step 11: Square root of 164836 is 406.


Final state: Answer 406

Abacus state transition. (Click to Zoom)



Next article is also about Double-root method.


Related articles:

How to solve Cube root of 1729.03 using abacus? (Feynman v.s. Abacus man)
http://blog.goo.ne.jp/ktonegaw/e/cff5d6e7ecaa07230b9cc7af10b23aed

Index: Square root and Cube root using Abacus
http://blog.goo.ne.jp/ktonegaw/e/f62fb31b6a3a0417ec5d33591249451b


Please place your mouse on the buttons and click one by one. These are blog ranking sites.