七平方定理（垂心四面体の場合）

「四平方定理」を「一般の垂心四面体」へ拡張した「七平方定理」　2008.11.3(月)

☆　この「定理」は2008.10.30(木)に得たばかりである。

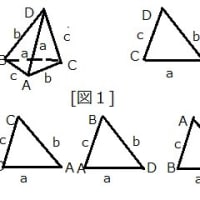
「垂心四面体ABCD」の6辺の長さを例によって、
BC＝a　，CA＝b　，AB＝c　，AD＝d　，BD＝e　，CD＝f　・・・(1.1.1)とし、
x＝((→AB)，(→AC))＝((→AB)，(→AD))＝((→AC)，(→AD))，
y＝((→BA)，(→BC))＝((→BA)，(→BD))＝((→BC)，(→BD))，
z＝((→CA)，(→CB))＝((→CA)，(→CD))＝((→CB)，(→CD)),
w＝((→DA)，(→DB))＝((→DA)，(→DC))＝((→DB)，(→DC))　・・・(1.1.2)とおくと、
x＝(b^2＋c^2－a^2)/2＝(c^2＋d^2－e^2)/2＝(d^2＋b^2－f^2)/2
y＝(c^2＋a^2－b^2)/2＝(e^2＋c^2－d^2)/2＝(a^2＋e^2－f^2)/2
z＝(a^2＋b^2－c^2)/2＝(b^2＋f^2－d^2)/2＝(f^2＋a^2－e^2)/2
w＝(d^2＋e^2－c^2)/2＝(f^2＋d^2－b^2)/2＝(e^2＋f^2－a^2)/2　・・・(1.1.3)
　kを　a^2＋d^2=b^2＋e^2=c^2＋f^2＝k^2　・・・(1.1.4)を満たす正の数とする。
また、△BCD　，△ACD　，△ABD　，△ABCの面積をそれぞれ、S_A　，S_B　，S_C　，S_D
とする。
このとき、次の関係式(1.1.5)があった。
　y＋z＝a^2　，x＋z＝b^2　，x＋y＝c^2　，
　x＋w＝d^2　，y＋w＝e^2　，z＋w＝f^2　　・・・(1.1.5)　
実は、
「四面体ABCD」が「垂心四面体」であること、つまり(1.1.2)　⇔　(1.1.5)　である。
このことは、また別の機会に示すつもりである。

さて、次の[定理2.1]が成り立ち、これは、「3直角四面体」で成立する「四平方定理」の
自然な拡張である。平方が7つあるので「七平方定理」と呼ぶことにする。

すなわち、
[定理2.1]　　　垂心四面体の「七平方定理」・・・・次の(2.1.5）を指す。
「垂心四面体ABCD」の6辺の長さを、
BC＝a　，CA＝b　，AB＝c　，AD＝d　、BD＝e　，CD＝f　・・・(2.1.1)とし、
x＝((→AB)，(→AC))＝((→AB)，(→AD))＝((→AC)，(→AD))，
y＝((→BA)，(→BC))＝((→BA)，(→BD))＝((→BC)，(→BD))，
z＝((→CA)，(→CB))＝((→CA)，(→CD))＝((→CB)，(→CD)),
w＝((→DA)，(→DB))＝((→DA)，(→DC))＝((→DB)，(→DC))　・・・(2.1.2)とおき、
　kを　a^2＋d^2=b^2＋e^2=c^2＋f^2＝k^2　・・・(2.1.3)を満たす正の数とする。
また、△BCD　，△ACD　，△ABD　，△ABCの面積をそれぞれ　S_A　，S_B　，S_C　，S_D
　とする。
このとき、aとd　，bとe　，cとfが3組の対辺であるが、

(1)　4[(S_A)^2＋(S_B)^2＋(S_C)^2＋(S_D)^2]＝(ad)^2＋(be)^2＋(cf)^2　・・・(2.1.4)

　　が成立する。

　　すなわち　(2S_A)^2＋(2S_B)^2＋(2S_C)^2＋(2S_D)^2＝(ad)^2＋(be)^2＋(cf)^2 ・・・(2.1.5）

(2)　「A－3直角四面体」では、上の(2.1.3)から
　　よく知られた、(S_A)^2＝(S_B)^2＋(S_C)^2＋(S_D)^2　・・・(2.1.6)　の式が

　　自然に導かれる。

「証明」
　(1)　2008.11.03(月)に、このBlogのあとにアップロードする予定のBlog「垂心四面体ABCDの垂心の
　ベクトルによる重心座標表現で見落としていた大事なこと」により、
　S_A　，S_B　，S_C　，S_Dは　それぞれ　△BCD　，△ACD　，△ABD　，△ABCの面積だから、

　4(S_A)^2＝zw＋yw＋yz　　・・・(2.2.1)，　4(S_B)^2＝zw＋xw＋xz　　・・・(2.2.2)
　4(S_C)^2＝yw＋xw＋xy　　・・・(2.2.3)，　4(S_D)^2＝yz＋xz＋xy　　・・・(2.2.4)

これらを加えれば、(1.1.5)を用いて
　　4[(S_A)^2＋(S_B)^2＋(S_C)^2＋(S_D)^2]
　＝(zw＋yw＋yz)＋(zw＋xw＋xz)＋(yw＋xw＋xy)＋(yz＋xz＋xy)
　＝2(xy＋xz＋xw＋yz＋yw＋zw）
　＝2{x(z＋w)＋y(x＋w)＋z(y＋w)}
　＝2{x(f^2)＋y(d^2)＋z(e^2)}
＝(2x)(f^2)＋(2y)(d^2)＋(2z)(e^2)　・・・(2.2.5)

ここで　(1.1.3)から　
　　2x＝b^2＋c^2－a^2　，2y＝c^2＋a^2－b^2　，2z＝a^2＋b^2－c^2　を代入して
　
　4[(S_A)^2＋(S_B)^2＋(S_C)^2＋(S_D)^2]
　　＝(b^2＋c^2－a^2)(f^2)＋(c^2＋a^2－b^2)(d^2)＋(a^2＋b^2－c^2)(e^2)
　
　ところで、(2.1.3)の　a^2＋d^2=b^2＋e^2=c^2＋f^2＝k^2　により、d^2，e^2，f^2を
　　k^2と、a^2，b^2，c^2で表せば、
　
　4[(S_A)^2＋(S_B)^2＋(S_C)^2＋(S_D)^2]
　＝(b^2＋c^2－a^2)(k^2－c^2)＋(c^2＋a^2－b^2)(k^2－a^2)＋(a^2＋b^2－c^2)(k^2－b^2)
　＝{(b^2＋c^2－a^2)＋(c^2＋a^2－b^2)＋(a^2＋b^2－c^2)}(k^2)
　　－[(c^2){(b^2)＋(c^2)－(a^2)}＋(a^2){(c^2)＋(a^2)－(b^2)}＋(b^2){(a^2)＋（b^2)－(c^2)}]
　＝{(a^2)＋(b^2)＋(c^2)}(k^2)
　　－[(bc)^2＋(c^4)－(ac)^2＋(ac)^2＋(a^4)－(ab)^2＋(ab)^2＋(b^4)－(bc)^2]
　＝{(a^2)＋(b^2)＋(c^2)}(k^2)－[(a^4)＋(b^4)＋(c^4)]
　＝(a^2){(k^2)－(a^2)}＋(b^2){(k^2)－(b^2)}＋(c^2){(k^2)－(c^2)}
　＝(a^2)(d^2)＋(b^2)(e^2)＋(c^2)(f^2)　
　＝(ad)^2＋(be)^2＋(cf)^2　
　
　ここで、(2.1.3)の　a^2＋d^2=b^2＋e^2=c^2＋f^2＝k^2　により
　(k^2)－(a^2)＝(d^2)　，(k^2)－(b^2)＝(e^2)　，(k^2)－(c^2)＝(f^2）を用いた。
　こうして　(2.1.4)の

　4[(S_A)^2＋(S_B)^2＋(S_C)^2＋(S_D)^2]＝(ad)^2＋(be)^2＋(cf)^2
　
　が導かれた。
次に
　(2)を示そう。
　　「A－3直角四面体ABCD」は、∠BAC＝∠BAD＝∠CAD＝90度の四面体で、これは「垂心H」が
　「頂点A」になる特殊な「垂心四面体」であった。
　よって　上の(1.1.2)の　x＝0　であって、
　x＝((→AB)，(→AC))＝((→AB)，(→AD))＝((→AC)，(→AD))＝0
　これは(1.1.3)から、
　b^2＋c^2－a^2＝c^2＋d^2－e^2＝d^2＋b^2－f^2＝0　，
　a^2＝b^2＋c^2　，e^2＝c^2＋d^2　，f^2＝b^2＋d^2　・・・(2.3.1)
　ゆえに　a^2，e^2，f^2は　b^2　，c^2　,　d^2　で表される。
　よって
　△ABCは∠BAC＝90度の直角三角形、△ABDは∠BAD＝90度の直角三角形，
　△ACDは∠CAD＝90度の直角三角形であり、
　S_D＝(bc)/2　，S_C＝(cd)/2　，S_B＝(bd)/2　ゆえに
　bc＝2(S_D)　，cd＝2(S_C)　，bd＝2(S_B)　・・・(2.3.2)　である。
さて、
(1)で証明した公式(2.1.4)の右辺に(2.3.1)を代入すれば、
　(2.1.4)の右辺＝(a^2)(d^2)＋(b^2)(e^2)＋(c^2)(f^2)
　　　　　　　 ＝(b^2＋c^2)(d^2)＋(b^2)(c^2＋d^2)＋(c^2)(b^2＋d^2)
　　　　　　　 ＝2{(bd)^2＋(cd)^2＋(bc)^2}　・・・(2.3.3)
　　これに　(2.3.2)を代入すれば、
(2.1.4)の右辺＝8[(S_B)^2＋(S_C)^2＋(S_D)^2]となる。
　よって　(2.1.4)式は
　4[(S_A)^2＋(S_B)^2＋(S_C)^2＋(S_D)^2]＝8[(S_B)^2＋(S_C)^2＋(S_D)^2]　となる。

　ゆえに　4(S_A)^2＝4[(S_B)^2＋(S_C)^2＋(S_D)^2]

　すなわち　(S_A)^2＝(S_B)^2＋(S_C)^2＋(S_D)^2

　となり、(2.1.6)式が自然に導かれた。

　（証明　終わり）