算額(その202)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額1(105)
長野県伊那市東春近 春近神社 文政4年(1821)
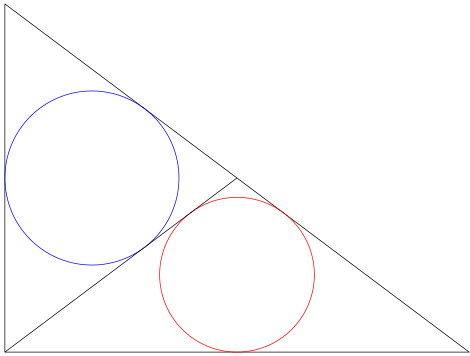
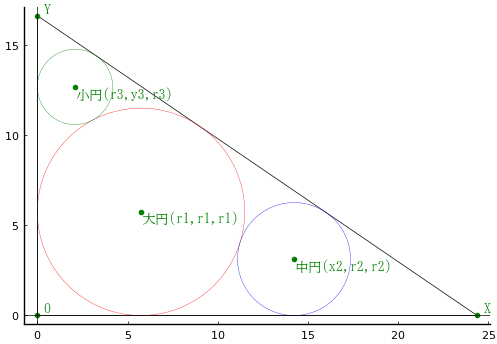
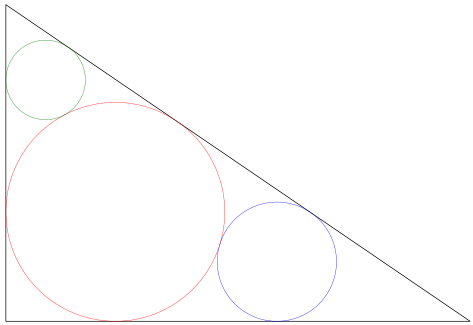
直線上に大円,中円,小円がある。それぞれの円は直線,垂直線,斜線に接している。3 個の円の径の和が 54 寸,小円を含む鉤股弦の和が 30 寸のとき,小円の径を求めよ。
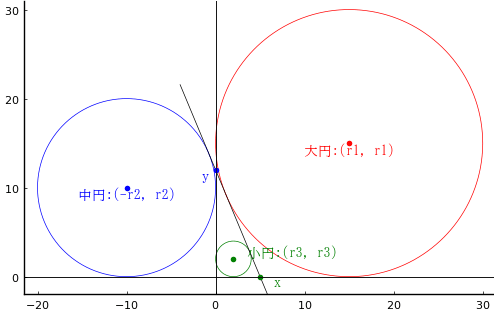
大円,中円,小円の半径をそれぞれ r1, r2, r3 とおく。また,鉤股の長さをそれぞれ x, y とおく。
using SymPy
function distance(x1, y1, x2, y2, x0, y0)
p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
l = sympy.Line(p1, p2)
l.distance(sympy.Point(x0, y0))^2 # 二乗距離を返す!!
end;
@syms r1::positive, r2::positive, r3::positive, x::positive, y::positive;
eq1 = distance(0, y, x, 0, r1, r1) - r1^2
eq2 = distance(0, y, x, 0, -r2, r2) - r2^2
eq3 = distance(0, y, x, 0, r3, r3) - r3^2
eq4 = 2(r1 + r2 + r3) - 54
eq5 = x + y + sqrt(x^2 + y^2) - 30;
# solve([eq1, eq2, eq3, eq4, eq5]);
println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
-r1^2 + (r1 - x*(r1*x - r1*y + y^2)/(x^2 + y^2))^2 + (r1 - y*(-r1*x + r1*y + x^2)/(x^2 + y^2))^2,
-r2^2 + (-r2 - x*(-r2*x - r2*y + y^2)/(x^2 + y^2))^2 + (r2 - y*(r2*x + r2*y + x^2)/(x^2 + y^2))^2,
-r3^2 + (r3 - x*(r3*x - r3*y + y^2)/(x^2 + y^2))^2 + (r3 - y*(-r3*x + r3*y + x^2)/(x^2 + y^2))^2,
2*r1 + 2*r2 + 2*r3 - 54,
x + y + sqrt(x^2 + y^2) - 30,
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(r1, r2, r3, x, y) = u
return [
-r1^2 + (r1 - x*(r1*x - r1*y + y^2)/(x^2 + y^2))^2 + (r1 - y*(-r1*x + r1*y + x^2)/(x^2 + y^2))^2,
-r2^2 + (-r2 - x*(-r2*x - r2*y + y^2)/(x^2 + y^2))^2 + (r2 - y*(r2*x + r2*y + x^2)/(x^2 + y^2))^2,
-r3^2 + (r3 - x*(r3*x - r3*y + y^2)/(x^2 + y^2))^2 + (r3 - y*(-r3*x + r3*y + x^2)/(x^2 + y^2))^2,
2*r1 + 2*r2 + 2*r3 - 54,
x + y + sqrt(x^2 + y^2) - 30,
]
end;
iniv = [big"20.0", 8, 3, 12, 8]
res = nls(H, ini=iniv)
(BigFloat[14.99999999999999999984666619116852447418727617700909974481543102428426836661943, 9.999999999999999998427131201068448021956451753434173348206627211441946563294198, 2.000000000000000001726202607763027503856272069556726906977939919601503399470133, 5.000000000000000001419534990100076452230824423574926396608810570956077428130958, 11.99999999999999999932144013561540591403353792037404330533967686003722496194269], true)
(r1, r2, r3, x, y) = res[1]
14.99999999999999999984666619116852447418727617700909974481543102428426836661943
9.999999999999999998427131201068448021956451753434173348206627211441946563294198
2.000000000000000001726202607763027503856272069556726906977939919601503399470133
5.000000000000000001419534990100076452230824423574926396608810570956077428130958
11.99999999999999999932144013561540591403353792037404330533967686003722496194269
r1 = 15.000; r2 = 10.000; r3 = 2.000; 鉤 = x = 5.000; 股 = y = 12.000; 弦 = 13.000
小円の半径は 2 である。元の単位でいえば,直径 4 寸。
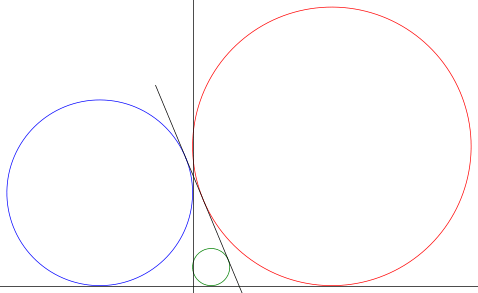
using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:blue, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function abline(x0, y0, slope, minx, maxx)
f(x0) = slope * x0 + y0
# println("slope = $slope $x0, $(f(x0)), $y0, $(f(y0))")
segment(minx, f(minx), maxx, f(maxx))
end
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, r3, x, y) = res[1]
@printf("r1 = %.3f; r2 = %.3f; r3 = %.3f; 鉤 = x = %.3f; 股 = y = %.3f; 弦 = %.3f\n",
r1, r2, r3, x, y, sqrt(x^2 + y^2))
plot(ylims=(-2, 31))
circle(r1, r1, r1)
circle(-r2, r2, r2, :blue)
circle(r3, r3, r3, :green)
abline(0, y, -y/x, -0.4r2, 2r1)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
if more == true
point(r1, r1, "大円:(r1, r1)", :red, :center)
point(-r2, r2, "中円:(-r2, r2)", :blue, :center)
point(r3, r3, " 小円:(r3, r3)", :green, :left, :bottom)
point(x, 0, " x", :green, :left)
point(0, y, "y ", :blue, :right)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;