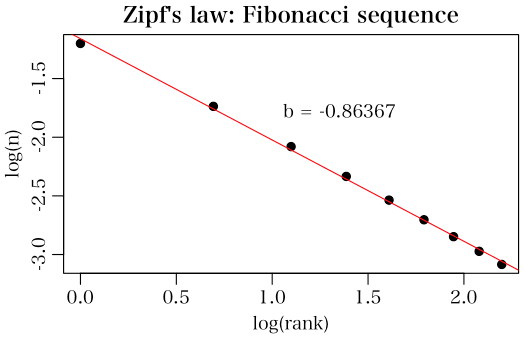
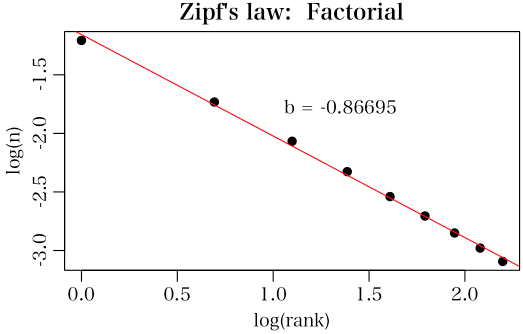
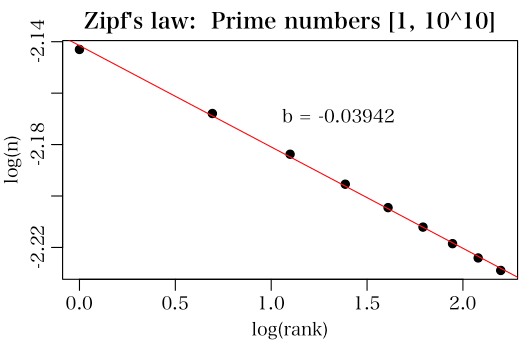
素数の先頭桁の数字の分布
Bartolo Luque and Lucas Lacasa: The first-digit frequencies of prime numbers and Riemann zeta zeros, Proc.R. Soc. A (2009) 465, 2197-2216.
について,誤解がずいぶんある。下の方に例。
論文を読めばわかることだけど,論文に書かれているのは「ベンフォードの法則」ではなく,「拡張されたベンフォードの法則」である。前者は '1' の出現比率はほぼ 30% というものだが,後者は,'1' の出現比率が一番高く,順次減少し,'9' の出現比率が最も低い。素数を探索する範囲を広くすればその違いは小さくなり,どの数字の出現比率も 1/9 に近づいていくというもの。
数式で書くと,前者は 数字 d の出現比率は P(d) =log10(1+1/d)。
後者は,P(d) = ((d+1)^(1-α) - d^(1-α)) / (10^(1-α)-1)。αは素数の探索範囲を [1,N] とすれば α(N) = 1/(log(N)-a)。α = 1 なら「ベンフォードの法則」,α = 0 なら一様分布(どの数字も等確率)。
N が大きくなるにつれ,それぞれの数字の出現比率は 1/9 に近づいていく。
[1, 10^8] にある素数は 5761455 個
素数の個数 比率 理論値
1 686048 0.11908 0.11891
2 664277 0.11530 0.11533
3 651085 0.11301 0.11307
4 641594 0.11136 0.11141
5 633932 0.11003 0.11011
6 628206 0.10904 0.10904
7 622882 0.10811 0.10813
8 618610 0.10737 0.10735
9 614821 0.10671 0.10665
[1, 10^9] にある素数は 50847534 個
素数の個数 比率 理論値
1 6003530 0.11807 0.11795
2 5837665 0.11481 0.11482
3 5735086 0.11279 0.11284
4 5661135 0.11134 0.11138
5 5602768 0.11019 0.11024
6 5556434 0.10928 0.10929
7 5516130 0.10848 0.10849
8 5481646 0.10781 0.10780
9 5453140 0.10724 0.10718
[1, 10^10] にある素数は 455052511 個
素数の個数 比率 理論値
1 53378283 0.11730 0.11720
2 52064915 0.11442 0.11442
3 51247361 0.11262 0.11265
4 50653546 0.11131 0.11136
5 50193913 0.11030 0.11034
6 49815418 0.10947 0.10949
7 49495432 0.10877 0.10878
8 49221187 0.10817 0.10815
9 48982456 0.10764 0.10760
以下のプログラムで計算したが,N = 10^10 までで数時間かかった。
> library(gmp)
> a = 1
> mx = 11
> tbl = matrix(0, mx, 9)
> freq = integer(9)
> for (i in 1:mx) {
+ N = 10^i
+ while(TRUE) {
+ a = nextprime(a)
+ b = as.integer(strsplit(as.character(a), "")[[1]][1])
+ if (a > N) {
+ a = a-1
+ tbl[i,] = freq
+ print(freq)
+ break
+ }
+ freq[b] = freq[b]+1
+ }
+ }
====== 誤解例,理解が不十分な例 ======
https://math-jp.net/2017/05/05/prime-benford/
> nを∞にしたときの極限をもとめたら、1から始まる素数の出現率になるはずですが、ものすごく収束がわるいようで30%になりそうではありませんでした
:
> 自分なりの結論ですが、素数はやはりベンフォードの法則のような偏りがあるのではなく一様に分布(大きくなっていくにつれ密度は薄くなっていきますが)していると考えられます。
1 で始まるものが 30% 近くになるなんて,原論文では言っていない。
極限では先頭桁の数字の出現比率はどの数字も 1/9 に近づいていくというのは正しい。
https://medium.com/@catindog/%E3%83%99%E3%83%B3%E3%83%95%E3%82%A9%E3%83%BC%E3%83%89%E3%81%AE%E6%B3%95%E5%89%87-b1382b65165e
> 自然界の数字(新聞記事に登場する数字とか)を集めていくと、先頭の文字が1が多く9に行くに従って単調減少していくというものであるそうです
:
> 10^7 までの数字の中の素数に関して、先頭の文字のヒストグラムを作成します。一番きれいに成り立っていますね。
筆者は '1' が 30% とは一言も書いていない。'1' 〜 '9' まで,単調減少している,と書いているわけだが,これが「拡張されたベンフォードの法則」であるとは書いていない。
https://mzp.hatenadiary.org/entry/20090515/benford
> スペインの数学者がBartolo LuqueとLucas Lacasaは素数にもこの法則が当てはまることをこの度解明したそうだ(論文要旨)
:
> とりあえず5000までの素数で確認したけど、特にベンフォードの法則には従っていなかった。まあ、そんなに簡単に分かることだったら論文にもならないだろうし、当然な気もする。
孫引きで,当然ながら原論文を読んでいないので,ベンフォードの法則と拡張されたベンフォードの法則の違いに気づいてもいない。
https://science.srad.jp/story/09/05/13/0641229/
> 12桁の数の場合でもやっぱり、1xxxが2xxxの2倍近いくらいになるような、明確な違いは出ないですねえ。というより、比は均等に近くなっているような?
> もっと巨大な数の領域になると法則に従うのでしょうか。(なんだか、もっと均等になりそうなヨカン)
> それとも、私がなにか勘違いしているのでしょうか。数論詳しい方ツッコミお願いします。
ベンフォードの法則と拡張されたベンフォードの法則の違いに気づいていない。
> 論文では、素数の先頭桁の分布がある意味で generalized Benford's law という法則に従っていることを示しているようです。 generalized Benford's law は Benford's law の一般化であり、 Benford's law そのものではありません。 generalized Benford's law とは何かとか、「ある意味で」とはどういう意味かとかは、僕には説明できません。知りたければ論文を読んでください。
「ボクには説明できません」なら,しかたないね。
> 直感的には桁の限界までの範囲で全部数えれば、どれも1/9、つまり11%になりそうな気がした。素数は違うか。
原論文を読んでいないので,ベンフォードの法則と拡張されたベンフォードの法則の違いに気づいていない。