算額（その395）

算額（その395）

東京都府中市 大國魂神社 明治18年(1885)
佐藤健一『多摩の算額』
山口正義『やまぶき』第8号
https://yamabukiwasan.sakura.ne.jp/ymbk8.pdf

半円の中に大円，小円，甲円，乙円，丙円が入っている。甲円，乙円の直径がそれぞれ 36 寸，22 寸のとき，丙円の直径を求めよ。

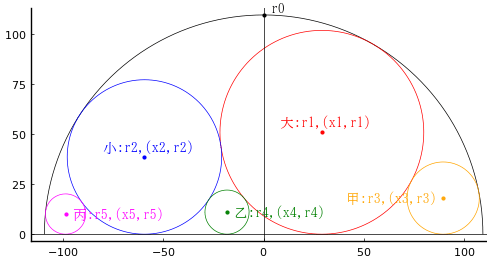
半円の半径と中心座標を r0, (0, 0)
大円の半径と中心座標を r1, (x1, r1)
小円の半径と中心座標を r2, (x2, r2)
甲円の半径と中心座標を r3, (x3, r3)
乙円の半径と中心座標を r4, (x4, r4)
丙円の半径と中心座標を r5, (x5, y5)
として，以下の連立方程式を立て，nlsove() で数値解を求める。

include("julia-source.txt");

using SymPy

@syms r0::positive, r1::positive, x1::positive, r2::positive,
     x2::negative, r3::positive, x3::positive, r4::positive,
     x4::negative, r5::positive, x5::negative;

(r3, r4) = (Sym(36), Sym(22)) .// 2
eq1 = (x1 - x2)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = (x3 - x1)^2 + (r1 - r3)^2 - (r1 + r3)^2
eq3 = (x1 - x4)^2 + (r1 - r4)^2 - (r1 + r4)^2
eq4 = (x4 - x2)^2 + (r2 - r4)^2 - (r2 + r4)^2
eq5 = (x2 - x5)^2 + (r2 - r5)^2 - (r2 + r5)^2
eq6 = x1^2 + r1^2 - (r0 - r1)^2
eq7 = x2^2 + r2^2 - (r0 - r2)^2
eq8 = x3^2 + r3^2 - (r0 - r3)^2
eq9 = x5^2 + r5^2 - (r0 - r5)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9])

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-63")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-63")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r0, r1, x1, r2, x2, x3, x4, r5, x5) = u
   return [
       (r1 - r2)^2 - (r1 + r2)^2 + (x1 - x2)^2,  # eq1
       (r1 - 18)^2 - (r1 + 18)^2 + (-x1 + x3)^2,  # eq2
       (r1 - 11)^2 - (r1 + 11)^2 + (x1 - x4)^2,  # eq3
       (r2 - 11)^2 - (r2 + 11)^2 + (-x2 + x4)^2,  # eq4
       (r2 - r5)^2 - (r2 + r5)^2 + (x2 - x5)^2,  # eq5
       r1^2 + x1^2 - (r0 - r1)^2,  # eq6
       r2^2 + x2^2 - (r0 - r2)^2,  # eq7
       x3^2 - (r0 - 18)^2 + 324,  # eq8
       r5^2 + x5^2 - (r0 - r5)^2,  # eq9
   ]
end;

iniv = [big"76.0", 34.0, 24.0, 32.0, -36.0, 60.0, -4.0, 12.0, -70.0]
res = nls(H, ini=iniv);
println(res);

  (BigFloat[109.2759607781864242781305327440617590523959228887413843855648291428112275807799, 50.78632222480445137700303498597358678562931717751496146783878544338869690961004, 29.0135708416527090497508430387449613589229832428047177392913207362097294847525, 38.48830848061307241285693076285644633867531725256882355802544542966271346448629, -59.40994721511970583145682953216998977779327580589532321869496230814697858668088, 89.48352371236297305829391802881040814933023875202264524826791200242400134239185, -18.25796581510720064785824833255286994844925646259226400277467085047377787714211, 10.0405052747635702369533443385048324890519598382837919173533224253202548503772, -98.72620666671672609506542347825094825128246061329118501178770677156669483447183], true)

r0 = 109.276;  r1 = 50.7863;  x1 = 29.0136;  r2 = 38.4883;  x2 = -59.4099;  x3 = 89.4835;  x4 = -18.258;  r5 = 10.0405;  x5 = -98.7262
丙円の直径 = 20.081

術を読み解くと以下のようである。
『8の平方根から1を引き天とする。乙円径を甲円径で割ったものの平方根をとり天を引き二乗したもので，乙円径を割る』

(乙円径, 甲円径) = (22, 36)
天 = √8 - 1
乙円径/(√(乙円径/甲円径) - 天)^2

   20.08101054952714

確かに数値解と同じになる。

2res[1][8]

   20.08101054952714047390668867700966497810391967656758383470664485064050970075439

using Plots

function draw(more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, r1, x1, r2, x2, x3, x4, r5, x5) = res[1]
   (r3, r4) = (36, 22) .// 2
   @printf("r0 = %g;  r1 = %g;  x1 = %g;  r2 = %g;  x2 = %g;  x3 = %g;  x4 = %g;  r5 = %g;  x5 = %g\n", r0, r1, x1, r2, x2, x3, x4, r5, x5)
   @printf("丙円の直径 = %g\n", 2r5)
   plot()
   circle(0, 0, r0, :black, beginangle=0, endangle=180)
   circle(x1, r1, r1)
   circle(x2, r2, r2, :blue)
   circle(x3, r3, r3, :orange)
   circle(x4, r4, r4, :green)
   circle(x5, r5, r5, :magenta)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       point(x1, r1, " 大:r1,(x1,r1)", :red, :center, :bottom, delta=delta)
       point(x2, r2, " 小:r2,(x2,r2)", :blue, :center, :bottom, delta=delta)
       point(x3, r3, "甲:r3,(x3,r3) ", :orange, :right, :vcenter)
       point(x4, r4, " 乙:r4,(x4,r4)", :green, :left, :vcenter)
       point(x5, r5, " 丙:r5,(x5,r5)", :magenta, :left, :vcenter)
       point(0, r0, " r0", :black, :left, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;