算額（その347）

算額（その347）

岐阜県大垣市赤坂町 金生山明星輪寺 元治2年(1865)
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF

菱形の中に交わる赤円が 2 個，白円が 2 個，青円が 5 個入っている。白円の直径が与えられているとき，青円の直径を求めよ。

菱形の中心を原点とし，縦，横の対角線の長さをそれぞれ 2y, 2x とする。
菱形の一辺の長さを z とする。z = sqrt(x^2 + y^2) である。
青，白，赤の円の直径を r1, r2, r3 とする。
上の青円の中心座標を (0, y1) とする。
右の青円の中心座標は (2r1 + 2r2, 0)
右の白円の中心座標は (r1 + r2, 0)
右の赤円の中心座標は (r1 + 2r2 - r3, 0)
である。

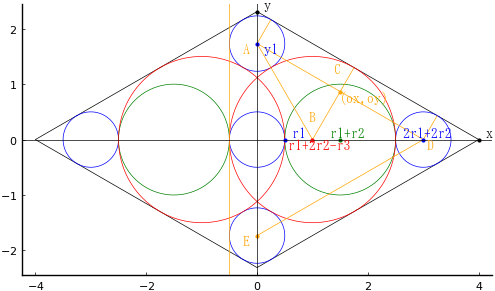
白円の半径を 1 として，連立方程式をたてる。簡単な4元連立方程式であるが，solve() で一度に求めるのは無理である。nlsolve() で数値解を求める過程について後半に記す。

しかし，図の見方を変えることにより，3 つの円の関係は非常に簡単に求めることができる。

1. 右の赤円の左端が接する y 軸に平行な補助線を引けば，三角ADEは正三角形になる。
2. ⊿ABC は直角三角形になる
   a. AB は青円と赤円の中心を結ぶ線分で，長さは r1 + r3
   b. AC は菱形の辺に平行な線分で，長さは 2sqrt(r1\*r3)
   c. BC は x 軸に 60°で交わる線分で，長さは AB/2
3. 赤円の直径は青円の直径と白園の直径の和に等しい。

これらの関係について連立方程式をたてる。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, r3::positive
eq1 = (r1 + r3)^2/4 + 4r1*r3 - (r1 + r3)^2
eq2 = r1 + r2 - r3
res = solve([eq1, eq2], (r1, r3))

   1-element Vector{Tuple{Sym, Sym}}:
    (r2/2, 3*r2/2)

r1 は r2 の 1/2，r3 はr2 の 3/2 である。

白円の直径が与えられるので，r1, r3 は確定され，図を描くために必要なのは，菱形の縦横の対角線の長さと上にある青円の中心の y 座標だけである。

白円の半径 r2 = 1 とすれば，青円，赤円の半径は r1 = 1/2, r3 = 3/2 である。

using SymPy

@syms r1::positive, r2::positive, r3::positive,
     x::positive, y::positive, y1::positive
(r1, r2, r3) = (1//2, 1, 3//2)
eq1 = (r1 + 2r2 - r3)^2 + y1^2 - (r1 + r3)^2
eq2 = (r1*y/x + 4sqrt(Sym(r1*r3)) + r1*x/y)^2 - x^2 - y^2
eq3 = r3*x - y*(2sqrt(Sym(r1*r3)) + r1*x/y)
solve([eq1, eq2, eq3], (x, y, y1))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (4, 4*sqrt(3)/3, sqrt(3))

using Plots

function draw()
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3) = (1//2, 1, 3//2)
   (x, y, y1) = (4, 4*sqrt(3)/3, sqrt(3))
   plot([x, 0, -x, 0, x], [0, y, 0, -y, 0], color=:black, lw=0.5)
   circle(0, 0, r1, :blue)
   circle(2r1 + 2r2, 0, r1, :blue)
   circle(-2r1 - 2r2, 0, r1, :blue)
   circle(0, y1, r1, :blue)
   circle(0, -y1, r1, :blue)
   circle(r1 + r2, 0, r2, :green)
   circle(-r1 - r2, 0, r2, :green)
   circle(r1 + 2r2 - r3, 0, r3)
   circle(-r1 - 2r2 + r3, 0, r3)
   plot!(showaxis=false)
end;
draw()

---

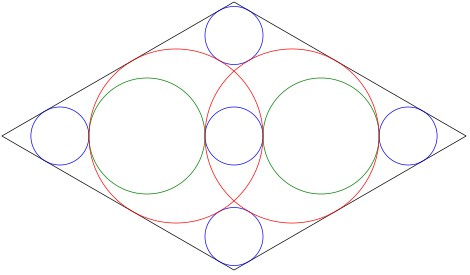
円の大きさの関係と図を描くために必要なパラメータを一括して求める

solve() では無理なので，nlsolve() で数値街を求める。

using SymPy

@syms r1, r2, r3, x, y, y1
@syms r1::positive, r2::positive, r3::positive, x::positive, y::positive, y1::positive

r2 = 1
r3 = r1 + r2

eq1 = (r1 + 2r2 - r3)^2 + y1^2 - (r1 + r3)^2
eq2 = (r1*y/x + 4sqrt(r1*r3) + r1*x/y)^2 - x^2 - y^2
eq3 = r3*x - y*(2sqrt(r1*r3) + r1*x/y)
eq4 = r1*sqrt(x^2 + y^2) - y*(x - 2r1 - 2r2);

# solve([eq1, eq2, eq3, eq4], (r1, x, y, y1))

println(eq1, ",  # eq1")
println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4")

   y1^2 - (2*r1 + 1)^2 + 1,  # eq1
   -x^2 - y^2 + (4*sqrt(r1)*sqrt(r1 + 1) + r1*x/y + r1*y/x)^2,  # eq2
   x*(r1 + 1) - y*(2*sqrt(r1)*sqrt(r1 + 1) + r1*x/y),  # eq3
   r1*sqrt(x^2 + y^2) - y*(-2*r1 + x - 2),  # eq4

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r1, x, y, y1) = u
   return [
       y1^2 - (2*r1 + 1)^2 + 1,  # eq1
       -x^2 - y^2 + (4*sqrt(r1)*sqrt(r1 + 1) + r1*x/y + r1*y/x)^2,  # eq2
       x*(r1 + 1) - y*(2*sqrt(r1)*sqrt(r1 + 1) + r1*x/y),  # eq3
       r1*sqrt(x^2 + y^2) - y*(-2*r1 + x - 2),  # eq4
   ]
end;

iniv = [big"0.45", 4.1, 2.2, 1.6]
res = nls(H, ini=iniv);
println(res);

   (BigFloat[0.5000000000000000000002647732231042221299746017703653458755774117300395986631534, 4.00000000000000000000150018442196727793019547881937562510553208700008372428873, 2.309401076758503058036288681801685476240636088014479770497112246296876844518601, 1.732050807568877293528878493906762400441924270519252071343713219148935154969712], true)

r1 = 0.5;  x = 4;  y = 2.3094;  y1 = 1.73205
x/y = 1.73205;  x/r2 = 4
白円直径 = 2;  赤円直径 = 3;  青円直径 = 1
青円の直径は白円の直径の 1/2 である。
なお，菱形は横の対角線の長さが縦の対角線の長さの √3 倍なので，正三角形を二個くっつけたものである。

using Plots

function draw(more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1
   (r1, x, y, y1) = [0.5, 4, 2.30940107675850305803, 1.73205080756887729352]  # res[1]
   r3 = r1 + r2
   @printf("r1 = %g;  x = %g;  y = %g;  y1 = %g\n", r1, x, y, y1)
   @printf("x/y = %g;  x/r2 = %g\n", x/y, x/r2)
   @printf("白円直径 = %g;  赤円直径 = %g;  青円直径 = %g\n", 2r2, 2r3, 2r1)
   plot([x, 0, -x, 0, x], [0, y, 0, -y, 0], color=:black, lw=0.5)
   circle(0, 0, r1, :blue)
   circle(2r1 + 2r2, 0, r1, :blue)
   circle(-2r1 - 2r2, 0, r1, :blue)
   circle(0, y1, r1, :blue)
   circle(0, -y1, r1, :blue)
   circle(r1 + r2, 0, r2, :green)
   circle(-r1 - r2, 0, r2, :green)
   circle(r1 + 2r2 - r3, 0, r3)
   circle(-r1 - 2r2 + r3, 0, r3)
   if more
       vline!([-r1], color=:orange, lw=0.5)
       segment(0, y1, r1 + 2r2 - r3, 0, :orange)
       (ox, oy) = (r1 + 2r2 - r3 + (r3 - r1)*cos(pi/3), (r3 - r1)*sin(pi/3))
       segment(r1 + 2r2 - r3, 0, r1 + 2r2 - r3 + r3*cos(pi/3), r3*sin(pi/3), :orange)
       segment(2r1 + 2r2, 0, 0, y1, :orange)
       segment(2r1 + 2r2, 0, 0, -y1, :orange)
       segment(0, y1, r1*cos(pi/3), y1 + r1*sin(pi/3), :orange)
       segment(2r1 + 2r2, 0, 2r1 + 2r2 + r1*cos(pi/3), r1*sin(pi/3), :orange)
       point(ox, oy, "(ox,oy)", :orange)
       point(ox, oy, "C\n", :orange, :right, :bottom, mark=false)
       point(r1, 0, " r1", :blue, :left, :bottom)
       point(r1 + 2r2 - r3, 0, "  r1+2r2-r3", :red, :center, :top)
       point(r1 + 2r2 - r3, 0, "B\n", :orange, :center, :bottom, mark=false)
       point(r1 + r2, 0, "  r1+r2", :green, :center, :bottom)
       point(2r1 + 2r2, 0, " 2r1+2r2", :blue, :center, :bottom)
       point(2r1 + 2r2, 0, "  D", :orange, :center, :top, mark=false)
       point(x, 0, " x", :black, :left, :bottom)
       point(0, y1, " y1", :blue)
       point(0, y1, "A ", :orange, :right, mark=false)
       point(0, -y1, "E ", :orange, :right)
       point(0, y, " y", :black, :left, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;