Julia に翻訳--203 数量化 I 類

#==========
Julia の修行をするときに，いろいろなプログラムを書き換えるのは有効な方法だ。
以下のプログラムを Julia に翻訳してみる。

数量化 I 類
http://aoki2.si.gunma-u.ac.jp/R/qt1.html

ファイル名: qt1.jl　　関数名: qt1, printqt1, plotqt1

翻訳するときに書いたメモ

==========#

using Statistics, StatsBase, Rmath, LinearAlgebra, NamedArrays, Plots

function qt1(dat, y; vnames=[], vnamey="")
    dat = hcat(dat, y)
    nc, p = size(dat)
    ncat = p - 1
    length(vnames) > 0 || (vnames = ["x$i" for i = 1:ncat])
    vnamey != "" || (vnamey = "dep. var.")
    mx = [maximum(dat[:, i]) for i = 1:ncat]
    start = vcat(0, cumsum(mx)[1:ncat - 1])
    nobe = sum(mx)
    x = zeros(nc, nobe - ncat + 1)
    for i = 1:nc
        x0 = []
        for j = 1:ncat
            zeros0 = zeros(mx[j])
            zeros0[dat[i, j]] = 1
            append!(x0, zeros0[2:end])
        end
        x[i, :] = vcat(x0, dat[i, end])
    end
    a = cov(x)
    ndim = nobe - ncat
    B = a[1:ndim, 1:ndim] \ a[ndim + 1, 1:ndim]
    m = mean(x, dims=1)
    constant = m[ndim + 1] - (m[1:ndim]' * B)
    predicted = x[:, 1:ndim] * B .+ constant
    observed = x[:, ndim + 1]
    residuals = observed .- predicted
    s = sum(x, dims=1)
    en = 0
    coef = []
    coefnames = []
    for i = 1:ncat
        st = en + 1
        en = st + mx[i] - 2
        target = st:en
        tempmean = (s[target]' * B[target]) / nc
        constant = constant + tempmean
        append!(coef, -tempmean, B[target] .- tempmean)
        append!(coefnames, ["$(vnames[i]).$j" for j = 1:mx[i]])
    end
    append!(coef, constant)
    append!(coefnames, ["constant"])
    q = ["a", "b"]
    par = zeros(nc, ncat)
    for j in 1:nc
        en = 0
        for i in 1:ncat
            st = en + 1
            en = st + mx[i] - 2
            target = st:en
            par[j, i] = x[j, target]' * B[target]
        end
    end
    par = hcat(par, observed)
    r = cor(par)
    i = inv(r)
    d = diag(i)
    partialcor = (-i ./ sqrt.(d * d'))[ncat + 1, 1:ncat]
    partialt = abs.(partialcor) .* sqrt.((nc - ncat - 1) ./ (1 .- partialcor .^ 2))
    partialp = pt.(partialt, nc - ncat - 1, false) .* 2
    Dict(:coef => coef, :coefnames => coefnames,
         :r => r, :partialcor => partialcor, :partialt => partialt,
         :partialp => partialp, :predicted => predicted,
         :observed => observed, :residuals => residuals,
         :vnames => vnames, :vnamey => vnamey)
end

function printqt1(obj)
    println("\ncategory score\n", NamedArray(reshape(obj[:coef], :, 1),
        (obj[:coefnames], ["category score"])))
    names = vcat(obj[:vnames], obj[:vnamey])
    println("\ncorrelation coefficient\n", NamedArray(obj[:r], (names, names)))
    println("\npartial correlation coeficiennt\n",
        NamedArray(hcat(obj[:partialcor], obj[:partialt], obj[:partialp]),
        (obj[:vnames], ["partial corr.", "t value", "p value"])))
    println("\nprediction\n",
        NamedArray(hcat(obj[:observed], obj[:predicted], obj[:residuals]),
        (1:length(obj[:observed]), ["observed", "predicted", "residuals"])))
end

function plotqt1(obj; which = "categoryscore") # or "fitness"
    pyplot()
    if which == "categoryscore"
        coefficients = obj[:coef][end-1:-1:1]
        plt = bar(coefficients, orientation=:h, grid=false,
                  yshowaxis=false, yticks=false,
                  xlabel="category score", label="")
        cname = [" $s " for s in obj[:coefnames][end-1:-1:1]]
        align = [c > 0 ? :right : :left for c in coefficients]
        annotate!.(0, 1:length(cname), text.(cname, align, 8))
        vline!([0], color=:black, label="")
    else
        minx, maxx = extrema(vcat(obj[:predicted], obj[:observed]))
        w = 0.05(maxx - minx)
        minx -= w
        maxx += w
        plt = scatter(obj[:predicted], obj[:observed], grid=false,
                      tick_direction=:out, xlabel = "predicted",
                      ylabel = "observed", aspect_ratio = 1,
                      lims=(minx, maxx), size=(600, 600), label="")
        plot!([minx, maxx], [minx, maxx], label="")
    end
    display(plt)
end

dat = [ 1  2  2
        3  2  2
        1  2  2
        1  1  1
        2  3  2
        1  3  3
        2  2  2
        1  1  1
        3  2  2
        1  1  2];
y = [6837, 7397, 7195, 6710, 6670, 6279, 6601, 4929, 5471, 6164];
obj = qt1(dat, y)
printqt1(obj)
#=====

category score
10×1 Named Matrix{Any}
   A ╲ B │ category score
─────────┼───────────────
x1.1     │          199.4
x1.2     │         -215.6
x1.3     │         -382.6
x2.1     │         -610.2
x2.2     │          241.8
x2.3     │          310.8
x3.1     │         -195.0
x3.2     │          149.5
x3.3     │         -656.5
constant │         6425.3

correlation coefficient
4×4 Named Matrix{Float64}
    A ╲ B │        x1         x2         x3  dep. var.
──────────┼───────────────────────────────────────────
x1        │       1.0  -0.510664  -0.463184  -0.103277
x2        │ -0.510664        1.0   0.164788   0.440587
x3        │ -0.463184   0.164788        1.0   0.290518
dep. var. │ -0.103277   0.440587   0.290518        1.0

partial correlation coeficiennt
3×3 Named Matrix{Float64}
A ╲ B │ partial corr.        t value        p value
──────┼────────────────────────────────────────────
x1    │      0.308748       0.795121       0.456835
x2    │      0.500942        1.41777       0.206039
x3    │      0.358395       0.940354       0.383335

prediction
10×3 Named Matrix{Float64}
A ╲ B │     observed     predicted     residuals
──────┼─────────────────────────────────────────
1     │       6837.0        7016.0        -179.0
2     │       7397.0        6434.0         963.0
3     │       7195.0        7016.0         179.0
4     │       6710.0        5819.5         890.5
5     │       6670.0        6670.0           0.0
6     │       6279.0        6279.0           0.0
7     │       6601.0        6601.0  -9.09495e-13
8     │       4929.0        5819.5        -890.5
9     │       5471.0        6434.0        -963.0
10    │       6164.0        6164.0  -9.09495e-13
=====#

plotqt1(obj) # savefig("fig1.png")

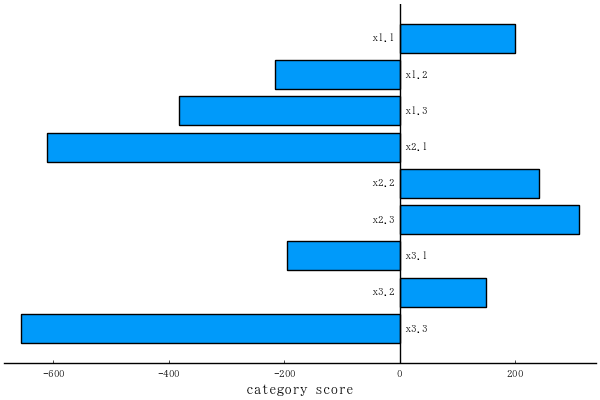
plotqt1(obj, which="fitness") # savefig("fig2.png")