算額（その1089）

算額（その1089）

四十三 岩手県一関市真滝 熊野白山滝神社 弘化3年(1846)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：楕円2個（楕円3個），正六角形（正三角形）

正六角形の中に等楕円（同じ大きさの楕円）を 2 個容れる。楕円の長径，短径が与えられたとき正六角形の一辺の長さを求めよ。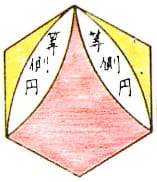

注：多分もとの算額の図でもそうなのであろうが，山村の図では楕円の書き方がまずく，図形を正確に表現できていない。正しくは下図のように，楕円は互いに接し，それぞれは正六角形の 2 辺にも接している。
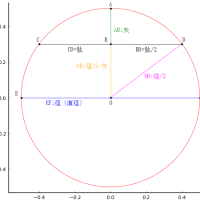
算額では楕円を 2 個としているが正六角形の中心を点対称として，3 個の楕円を考えるとわかりやすい。しかも，第 3 の楕円は長径，短径が水平，垂直なので，計算しやすい。以下では，第 3 の楕円について解く。

原点を 第 3 の楕円の中心に置く。
楕円の長半径，短半径を a, b
正六角形の一辺の長さを l
楕円同士の接点（符号は違うが正六角形の一辺との接点と同じ）の座標を (x0, y0)
とおき，以下の連立方程式を解く。
作図する際には，(x0, y0) は不要である。

include("julia-source.txt")

using SymPy
@syms a::positive, b::positive, l::positive,
     x0::positive, y0::positive
@syms a, b, l, x0, y0
eq1 = x0^2/a^2 + y0^2/b^2 - 1
eq2 = -b^2*x0/(a^2*y0) + 1/√Sym(3)
eq3 = √Sym(3)y0 - √Sym(3)l/2 + x0
res = solve([eq1, eq2, eq3], (l, x0, y0))[2];

l，x0，y0 は以下のように，少し簡約化できる。

(2√Sym(3)sqrt(a^2 + 3b^2)/3, a^2/sqrt(a^2 + 3b^2), √Sym(3)b^2/sqrt(a^2 + 3b^2));

たとえば，長半径 が 4 寸，短半径が 2 寸のとき，正六角形の一辺の長さは 6.110100926607786 寸である。

a = 4
b = 2
2√3sqrt(a^2 + 3b^2)/3

   6.110100926607786

術は「邪術」である。これでは答えは出ない。
たとえば，長径と短径がともに 1 である（これは，円である）ときに以下のように 0.8611513361757016 になる。

長径 = 1
短径 = 1
位 = 長径^2 + 短径^2
A = (sqrt(位^2 + 2長径^2*短径^2) + 位)/6
sqrt(A)

   0.8611513361757016

図を描いてみると正六角形の一辺の長さは 0.8611513361757016 ではないことが明らかである。
円の半径が 1/2 なので，正三角形の一辺の長さは 2 になる。更に，正六角形の一辺の長さは，正三角形の一辺の長さの半分の 2/√3 倍で 1.1547005383792515 になる。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (4, 2)
   (l, x0, y0) = (2*sqrt(3)*sqrt(a^2 + 3*b^2)/3, a^2/sqrt(a^2 + 3*b^2), sqrt(3)*b^2/sqrt(a^2 + 3*b^2))
   @printf("l = %.15g;  x0 = %g;  y0 = %g\n", l, x0, y0)
   plot([√3l/2, 0, -√3l/2, √3l/2], [0, 3l/2, 0, 0], color=:blue, lw=0.5)
   plot!(l .* [0, √3/2, √3/2, 0, -√3/2, -√3/2, 0],
       l .* [-1/2, 0, 1, 3/2, 1, 0, -1/2], color=:green, lw=0.5)
   circle(0, l/2, l)
   ellipse(0, 0, a, b, color=:magenta)
   ellipse(l/2*cosd(30), l/2*sind(30) + l/2, a, b, φ=120, color=:magenta)
   ellipse(-l/2*cosd(30), l/2*sind(30) + l/2, a, b, φ=240, color=:magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "", :magenta)
       point(l/2*cosd(30), l/2*sind(30) + l/2, "", :magenta)
       point(-l/2*cosd(30), l/2*sind(30) + l/2, "", :magenta)
       point(0, b, "b", :magenta, :center, :bottom, delta=delta/2)
       point(a, 0, " a", :magenta, :left, :bottom)
   end
end;