算額（その243）

算額（その243）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（227)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

正三角形とそれに内接する円 2 本の（左右対称な）斜線に接する貞円 3 個，元円，亨円，利円が 1 個ずつある。貞円の径を知って亨円の径を求めよ。

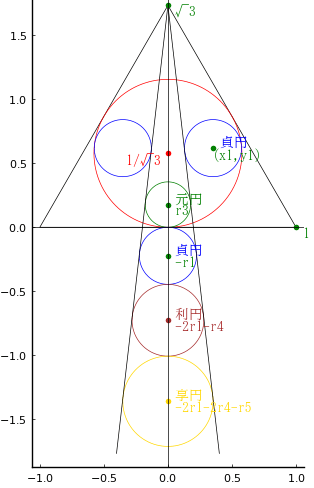
正三角形の一辺の長さを 1 とする。
右側の貞円の半径，中心座標を r1, (x1, y1)
下側の貞円の半径，中心座標を r1, (-r1, 0)
内接円の半径，中心座標を r2, (0, r2)
元円の半径，中心座標を r3, (0, r3)
利円の半径，中心座標を r4, (0, -2r1-r4)
亨円の半径，中心座標を r5, (0, -2r1-2r4-r5)
とする。
2 本の斜線の狭角の 1/2 を θとすると，sinθ= (√3 - r2) / (r2 - 2r1) である。
また，r2 = 1/√3，x1 = (r1 + r2)cos(π/6), y1 = (r1 + r2)sin(π/6) + r2 である。
以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, x1::positive, y1::positive, r2::positive, r3::positive, r4::positive, r5::positive;

r2 = 1/√Sym(3)
sinθ = (r2 - 2r1) / (√Sym(3) - r2)
cosθ = sqrt(1 - sinθ^2);

sqrt3 = sqrt(Sym(3))
eq1 = (sqrt3 + r1)sinθ - r1 |> expand
eq2 = (sqrt3 - r3)sinθ - r3 |> expand
eq3 = (sqrt3 + 2r1 + r4)sinθ - r4 |> expand
eq4 = (sqrt3 + 2r1 + 2r4 + r5)sinθ - r5 |> expand;

(r1, r3, r4, r5) = solve([eq1, eq2, eq3, eq4], (r1, r3, r4, r5))[1]

   (-7*sqrt(3)/12 + sqrt(219)/12, -sqrt(219)/24 + 11*sqrt(3)/24, -sqrt(219)/9 + 10*sqrt(3)/9, -83*sqrt(3)/54 + 11*sqrt(219)/54)

   r1 = 0.22286;  r2 = 0.57735;  r3 = 0.17725;  r4 = 0.28021; r5 = 0.35231
   x1 = 0.35218;  y1 = 0.61776

亨円と貞円の半径（直径）の比を求める。

(r5 / r1) |> simplify |> println

   37/18 - sqrt(73)/18

術では「74 から 292 の平方根を引き，貞円の径を掛け，36 で割れば亨円の径を得る」と言っている。分子分母を2倍しているだけで，同じである。

(74 - sqrt(Sym(292)))/36 |> simplify |> println

   37/18 - sqrt(73)/18

新しい術「37 から 73 の平方根を引き，貞円の径を掛け，18 で割れば亨円の径を得る」

(r5 / r1) * 0.22286 |> N

   0.352316851406585282011764975423176304679348938046109770889125810268254317780704

ついでに，利円，元円，内接円の半径（直径）と貞円の半径（直径）の関係を求めておく。

r4 / r1 |> simplify |> println  # 利円

   -1/6 + sqrt(73)/6

r3 / r1 |> simplify |> println  # 元円

   1/12 + sqrt(73)/12

r2 / r1 |> simplify |> println  # 内接円

   7/6 + sqrt(73)/6

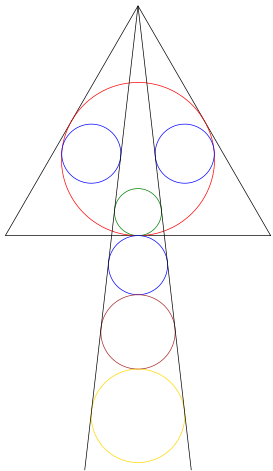
using Plots
using Printf
function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   sqrt3 = sqrt(3)
   r2 = 1/sqrt3
   (x1, r1, r3, r4, r5) = (5/24 + sqrt(2)*sqrt(61 - 7*sqrt(73))/6 + sqrt(73)/24, -7*sqrt(3)/12 + sqrt(219)/12, -sqrt(219)/24 + 11*sqrt(3)/24, -sqrt(219)/9 + 10*sqrt(3)/9, -83*sqrt(3)/54 + 11*sqrt(219)/54)
   sinθ = (r2 - 2r1) / (sqrt3 - r2)
   cosθ = sqrt(1 - sinθ^2)
   tanθ = sinθ / cosθ
   x1 = (r2 - r1)cosθ
   y1 = (r2 - r1)sinθ + r2
   @printf("r1 = %.5f;  r2 = %.5f;  r3 = %.5f;  r4 = %.5f; r5 = %.5f\n", r1, r2, r3, r4, r5)
   @printf("x1 = %.5f;  y1 = %.5f\n", x1, y1)
   plot([1, 0, -1, 1], [0, sqrt3, 0, 0], color=:black, lw=0.5)
   circle(0, r2, r2)
   circle(0, r3, r3, :green)
   circle(0, -r1, r1, :blue)
   circle(x1, y1, r1, :blue)
   circle(-x1, y1, r1, :blue)
   circle(0, -2r1-r4, r4, :brown)
   circle(0, -2r1-2r4-r5, r5, :gold)
   segment(0, sqrt3, 3.5tanθ, sqrt3 - 3.5)
   segment(0, sqrt3, -3.5tanθ, sqrt3 - 3.5)
   if more == true
       point(0, 1/sqrt3, "1/√3 ", :red, :right)
       point(x1, y1, "(x1,y1)")
       point(x1, y1, " 貞円", :blue, :left, :bottom, mark=false)
       point(1, 0, " 1")
       point(0, sqrt3, " √3")
       point(0, r3, " r3")
       point(0, r3, " 元円", :green, :left, :bottom, mark=false)
       point(0, -r1, " -r1")
       point(0, -r1, " 貞円", :blue, :left, :bottom, mark=false)
       point(0, -2r1-r4, " -2r1-r4", :brown)
       point(0, -2r1-r4, " 利円", :brown, :left, :bottom, mark=false)
       point(0, -2r1-2r4-r5, " -2r1-2r4-r5", :gold)
       point(0, -2r1-2r4-r5, " 亨円", :gold, :left, :bottom, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;