算額(その307)
「三重県に現存する算額の研究」福島完(2007/2/13)
https://mie-u.repo.nii.ac.jp/?action=repository_uri&item_id=7216
三重県伊賀市 永保寺 天保15年(1844)
問題文4
図のような五芒星を一本の糸で作る。中にできた正五角形の面積が 730925坪(7309.25平方寸)のとき,正五角形の一辺の長さと糸の長さを求めよ。
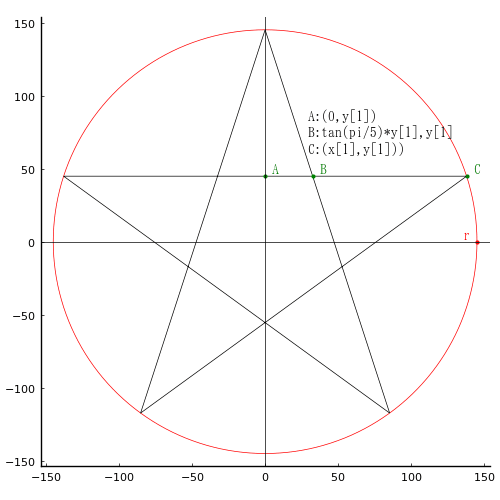
正五角形の一辺の長さを 2a,とする。この面積は (2a)^2\*sqrt(10\*sqrt(5) + 25)/4 である(注)。
五芒星が内接する外円の半径を r,五芒星の第1象限にある角の x 座標を x1 とする。
以下の連立方程式を解く(a だけが求まれば,あとは連鎖的に求まるので,連立方程式を解かなくてもよい)。
include("julia-source.txt");
using SymPy
@syms a::positive, r::positive, x1::positive
eq1 = a/(r*sin(PI/10)) - tan(PI/5)
eq2 = (2a)^2*sqrt(10sqrt(5) + 25)/4 - 7309.25
eq3 = x1 - r*cos(PI/10)
solve([eq1, eq2, eq3], (a, r, x1))
1-element Vector{Tuple{Sym, Sym, Sym}}:
(32.5898173447572, 145.157179706289, 138.052681646693)
外円の半径 = 145.157180寸
正五角形の一辺の長さ = 2a = 65.179635寸
糸の長さ = 10x1 = 1380.526816寸
using Plots
function draw(zoomin=false, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(a, r, x1) = (32.5898173447572, 145.157179706289, 138.052681646693)
delta = 2pi/5
x = zeros(5)
y = zeros(5)
for i in 1:5
θ = pi/2 + (i - 2)delta
x[i] = r*cos(θ)
y[i] = r*sin(θ)
end
b = tan(pi/5)*y[1]
@printf("外円の半径 = %.6f寸\n", r)
@printf("正五角形の一辺の長さ = %.6f寸\n", 2a)
@printf("糸の長さ = %.6f寸\n", 10x1)
plot()
circle(0, 0, r)
plot!(x[[1,3,5,2,4,1]], y[[1,3,5,2,4,1]], color=:black, lw=0.5)
if more
point(r, 0, "r ", :red, :right, :bottom)
point(0, y[1], " A", :green, :left, :bottom)
point(tan(pi/5)*y[1], y[1], " B", :green, :left, :bottom)
point(x[1], y[1], " C", :green, :left, :bottom)
annotate!(29, 75, text("A:(0,y[1])\nB:tan(pi/5)*y[1],y[1]\nC:(x[1],y[1]))", :left, 10))
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
x
cot(PI/5)*(x/2)^2 * 5 |> simplify |> println



























※コメント投稿者のブログIDはブログ作成者のみに通知されます