算額（その326）

算額（その326）

早坂平四郎:算額の一考察，苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf

正方形に関するもの
千葉県成田市 成田不動新勝寺光明堂 明治30年(1897)

正方形内に半円 2 個，等円 3 個を図のように入れる。正方形の一辺の長さを等円の半径で表わせ。

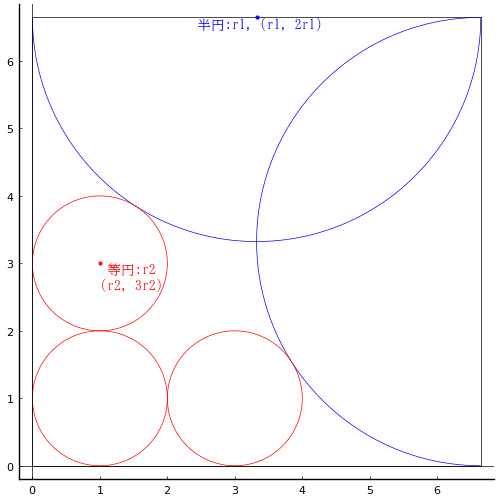
正方形の一辺の長さを 2r1 とする（半円の半径を r1 とする）。
等円の半径を r2 とする。
左上の半円と上の等円が接するという条件で，以下の方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive;

eq = (r1 - r2)^2 + (2r1 - 3r2)^2 - (r1 + r2)^2
solve(eq, r1) |> println

   Sym[r2*(4 - sqrt(7))/2, r2*(sqrt(7) + 4)/2]

二通りの解が得られるが，r1 = r2*(sqrt(7) + 4)/2 が題意を満たす。

すなわち，正方形の一辺の長さ 2r1 は等円の半径の 4 + √7 倍である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1
   r1 = (4 + √7)/2
   plot([0, 2r1, 2r1, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5)
   circle(r1, 2r1, r1, :blue, beginangle=180, endangle=360)
   circle(2r1, r1, r1, :blue, beginangle=90, endangle=270)
   circle(r2, r2, r2)
   circle(r2, 3r2, r2)
   circle(3r2, r2, r2)
   if more
       point(r1, 2r1, " 半円:r1, (r1, 2r1)", :blue, :center)
       point(r2, 3r2, " 等円:r2\n(r2, 3r2)", :red)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;