2変数が本質的に相関のある場合とない場合の時系列データの解析

時系列データの解析についてのコメントが流行っているのか...

「R: 時系列データ間の関係を状態空間モデルでみる」
「R: 時系列データ間の関係を状態空間モデルでみる（2）」 であるが...

状態空間モデルというのは，不勉強で知らなかったのだが，偏相関係数でも対応できるように思えたのでやってみた。

z を制御したときの x と y の間の偏相関係数を計算する関数

par.cor = function(x, y, z) {
     xy = cor(x, y)
     xz = cor(x, z)
     yz = cor(y, z)
     (xy-xz*yz)/sqrt((1-xz^2)*(1-yz^2))
}

第 1 部
本質的に無関係な x, y と，時間変数 z

> set.seed(1234)
>
> N.t = 60
> mu.x = numeric(N.t)
> x = numeric(N.t)
> mu.y = numeric(N.t)
> y = numeric(N.t)
> s1 = 2
> s2 = 1
>
> mu.x[1] = mu.y[1] = 10
>
> for (t in 1:(N.t - 1)) {
+   x[t] = rnorm(1, mu.x[t], s1)
+   mu.x[t + 1] = rnorm(1, mu.x[t] + 1, s2)
+   y[t] = rnorm(1, mu.y[t], s1)
+   mu.y[t + 1] = rnorm(1, mu.y[t] + 1, s2)
+ }
> x[N.t] = rnorm(1, mu.x[N.t - 1], s1)
> y[N.t] = rnorm(1, mu.y[N.t - 1], s1)
>
> z = 1:N.t # 時間変数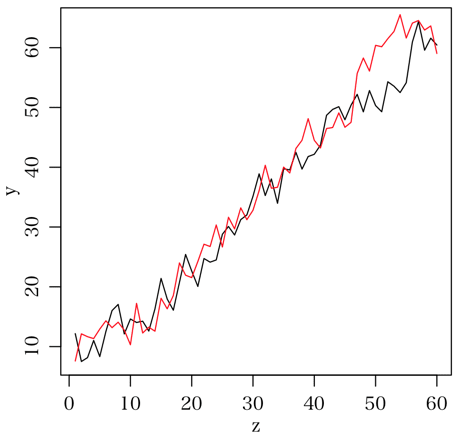


分析してみる。
 
> resid.x = lm(x ~ z)$residuals
> resid.y = lm(y ~ z)$residuals
> plot(resid.y ~ resid.x)
> text(-6, 6, sprintf("par.cor. = %.3f", par.cor(x, y, z)), pos=4)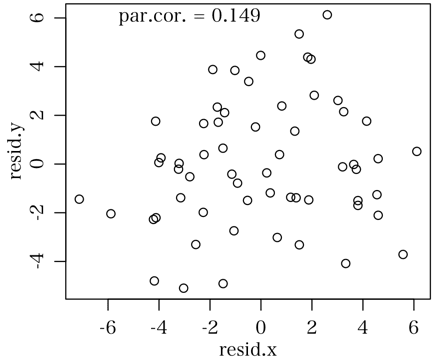



時間を制御したときの x, y 間の偏相関係数は小さいことがわかる。

> summary(lm(y ~ x+z))

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)   4.5894     0.8172   5.616 6.06e-07
x             0.1275     0.1117   1.141    0.259
z             0.8144     0.1175   6.934 4.10e-09

重回帰分析でも，x は y を説明しているとは言いがたい。z によって説明される。

===============================================

第 2 部
本質的に関連のある x, y と，時間変数 z は前のまま（元記事の変数名 y を  y2 に変更）

> # y2 は x から生成
> y2 = rnorm(N.t, x * 2, 8)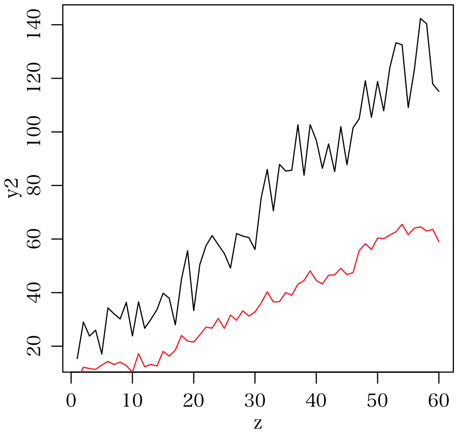



同じように分析してみる。
 
> resid.x = lm(x ~ z)$residuals
> resid.y2 = lm(y2 ~ z)$residuals
> plot(resid.y2 ~ resid.x)
> text(-6, 15, sprintf("par.cor. = %.3f", par.cor(x, y2, z)), pos=4)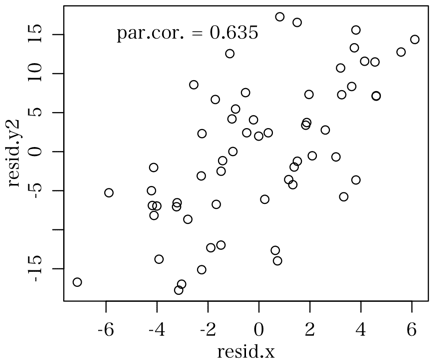



時間を制御したときの x, y2 間の偏相関係数は大きい（x と y2 には本質的な相関関係がある）。

> summary(lm(y2 ~ x + z))

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  3.09809    2.24666   1.379    0.173
x            1.90342    0.30705   6.199 6.77e-08
z            0.04705    0.32293   0.146    0.885

重回帰分析でも，x は y2 を有意に説明している。
それに反して，時間変数 z は y2 を説明していない（x が説明しているので，それで十分）。