算額（その477）

算額（その477）

宮城県丸森町小斎日向 鹿島神社 明治9年

徳竹亜紀子，谷垣美保: 2021年度の算額調査，仙台高等専門学校名取キャンパス 研究紀要，第 58 号, p.7-28, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2022/03/kiyo2022-2.pdf

円内に等円 2 個，菱形 2 個が入っている。等円の直径が与えられたとき，菱形の一辺の長さを求めよ。

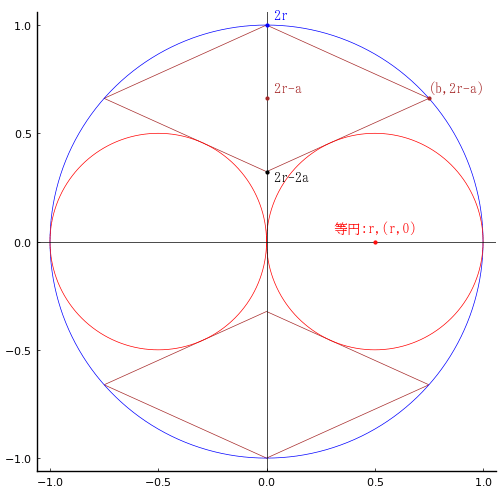
菱形の短い方の対角線の長さを 2a，長い方の対角線の長さを 2b とする。菱形の右の頂点の座標は (b, 2r - a) である。頂点は円周上にあるので，b = sqrt((2r)^2 - (2r - a)^2) である。

以下の方程式で a を求める。

include("julia-source.txt")

using SymPy
@syms a::positive, b::positive, r::positive;

b = sqrt((2r)^2 - (2r - a)^2)
eq = distance(0, 2r - 2a, b, 2r - a, r, 0) - r^2
res = solve(eq, a);

6 個の解が得られるが，2 番目のものが適解である。

すなわち，a = r*(2 - √7/2) である。

res[2] |> println

   r*(2 - sqrt(7)/2)

菱形の一辺の長さは sqrt(a^2 + b^2) = r*(√7 - 1) である。

@syms a::positive, b::positive, r::positive;
a = r*(2 - sqrt(Sym(7))/2)
b = sqrt((2r)^2 - (2r - a)^2)
sqrt(a^2 + b^2) |> simplify |> sympy.sqrtdenest |> println

   r*(-1 + sqrt(7))

等円の直径が 1 寸のとき，菱形の一辺の長さは 0.5(√7 - 1) = 0.8228756555322954 = 8分2厘2毛8糸有奇である。

0.5(√7 - 1) |> println

   0.8228756555322954

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1//2
   a = r*(2 - sqrt(7)/2)
   b = sqrt((2r)^2 - (2r - a)^2)
   length = r*(sqrt(7) - 1)
   @printf("a = %g; b = %g;  菱形の一辺の長さ = %g\n", a, b, length)
   plot([0, b,  0, -b, 0], [2r - 2a, 2r - a, 2r, 2r - a, 2r - 2a], color=:brown, lw=0.5)
   plot!([0, b,  0, -b, 0], [2a - 2r, a - 2r, -2r, a - 2r, 2a - 2r], color=:brown, lw=0.5)
   circle(0, 0, 2r, :blue)
   circle(r, 0, r)
   circle(-r, 0, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, 2r, " 2r", :blue, :left, :bottom, delta=delta/2)
       point(0, 2r - a, " 2r-a", :brown, :left, :bottom, delta=delta/2)
       point(b, 2r - a, "(b,2r-a)", :brown, :left, :bottom, delta=delta/2)
       point(0, 2r - 2a, " 2r-2a", :black, :left, :top)
       point(r, 0, "等円:r,(r,0)", :red, :center, :bottom, delta=delta)
   end
end;