算額（その770）

算額（その770）

神壁算法 天明8年戊申 二月 關流藤田貞資門人 細川能登守家士 渡邉金八源耀
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

正五角形に5本の斜線を入れ，内部に小さな正五角形を作り，できた 6 つの区画にそれぞれ同じ直径を持つ円を内接させる。
正五角形の一辺の長さが 533 寸 6 分のとき，等円の直径はいかほどか。

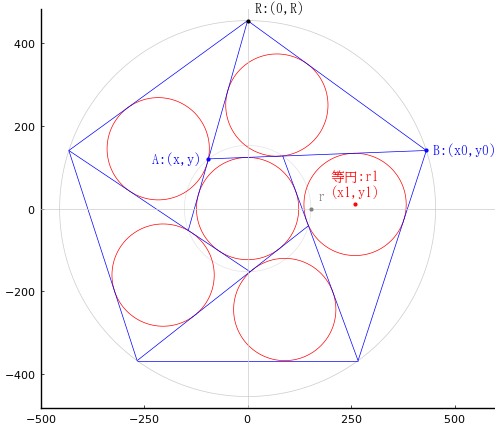
正五角形の一辺の長さを L，正五角形が内接する円の半径を R とする。
内側の正五角形が内接する円の半径を c，その一辺の長さを l とする。
等円の半径を r1 とする。
斜線と正五角形の一辺で作られる三角形 BAR において第二余弦定理を使う。
AR, AB, BR の長さを AR, AB, BR，また，A, B, R の座標を (x, y), (x0, y0), (0, R) とする。
ポイントは，斜線は外側の五角形の一辺と平行ではないということである。

include("julia-source.txt");

using SymPy
@syms L::positive, R::positive,
     x0::positive, y0::positive,
     x1::positive, y1::positive,
     x::negative, y::positive,
     AR::positive, l::positive, r1::positive
d18 = Sym(18)

R = L/2sind(2d18)
x0 = R*cosd(d18)
y0 = R*sind(d18)
c = sqrt(x^2 + y^2)

eq1 = (x0 - x)^2 + (y0 - y)^2 - (AR + l)^2
eq2 = x^2 + (R - y)^2 - AR^2
eq3 = AR^2 + (AR + l)^2 - 2AR*(AR + l)*cosd(4d18) - L^2
eq4 = dist(x0, y0, R*cosd(-3d18), R*sind(-3d18), x1, y1) - r1^2
eq5 = dist(x0, y0, x, y, x1, y1) - r1^2
eq6 = dist(x0, y0, x, y, 0, 0) - r1^2
eq7 = dist(c*cosd(atand(y, x) - 4d18), c*sind(atand(y, x) - 4d18), R*cosd(-3d18), R*sind(-3d18), x1, y1) - r1^2;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(par)
   (AR, l, x, y, x1, y1, r1) = par
   a = 2sqrt(5/8 - √5/8)
   b = √5/4 - 1/4
   g = L*sqrt(5/8 + √5/8)
   c = x - g/a
   d = L/2 - g/a
   e = x1 - g/a
   f = (atan(y/x)/pi + 1) - 2/5
   h = -L/a*((√5 + 1)/4 + b)
   i = sqrt(x^2 + y^2)
   j = i*cos(pi*f)
   k = i*sin(pi*f)
   m = -L*(√5 + 1)/4a - k
   n = L/2 - j
   o = (x1 - j)*n + (y1 - k)*m
   p = y - L*b/a
   q = y1 - L*b/a
   r = h^2 + d^2
   s = p^2 + c^2
   t = n^2 + m^2
   u = (L*b*p + g*c)/(s*a)
   return [
       (L*b/a - y)^2 + (g/a - x)^2 - (AR + l)^2,  # eq1
       x^2 + (L/a - y)^2 - AR^2,  # eq2
       AR^2 - 2AR*b*(AR + l) - L^2 + (AR + l)^2,  # eq3
       (y1 - L*b/a - (q*h + d*e)*h/r)^2 + (x1 - g/a - (q*h + d*e)*d/r)^2 - r1^2,  # eq4
       (y1 - L*b/a - (p*q + c*e)*p/s)^2 + (x1 - g/a - (p*q + c*e)*c/s)^2 - r1^2,  # eq5
       (p*u - L*b/a)^2 + (c*u - g/a)^2 - r1^2,  # eq6
       (x1 - n*o/t - j)^2 + (y1 - o*m/t - k)^2 - r1^2,  # eq7
   ]
end;

L = 5336//10
iniv = BigFloat[347.1, 179.5, -94.4, 119.9, 259.5, 10.0, 123.5]
res = nls(H, ini=iniv)

   ([347.0551765561487, 179.4560303257959, -94.42748155686841, 119.94507841468496, 259.51771893633804, 10.023199995813941, 123.50001782997607], true)

正五角形の一辺の長さが 533 寸 6 分のとき，等円の直径は 247 寸である。

その他のパラメータは以下のとおりである。

AR = 347.055;  x = -94.4275;  y = 119.945;  x1 = 259.518;  y1 = 10.0232;  r1 = 123.5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   L = 5336//10
   #l = 100
   R = L/2sind(2*18)
   x0 = R*cosd(18)
   y0 = R*sind(18)
   (AR, l, x, y, x1, y1, r1) = res[1]
   @printf("等円の直径 = %g\n", 2r1)
   @printf("AR = %g;  x = %g;  y = %g;  x1 = %g;  y1 = %g;  r1 = %g\n", AR, x, y, x1, y1, r1)
   r = sqrt(x^2 + y^2)
   θ = atand(y, x)
   ix = [r*cosd(72i + θ) for i in 0:5]
   iy = [r*sind(72i + θ) for i in 0:5]
   ox = [R*cosd(72i + 18) for i in 0:5]
   oy = [R*sind(72i + 18) for i in 0:5]
   plot()
   circle(0, 0, R, :gray80)
   circle(0, 0, r, :gray90)
   circle(0, 0, r1)
   rotate(x1, y1, r1, angle=72)
   for i in 1:5
       segment(ox[i], oy[i], ix[i], iy[i], :blue)
       segment(ox[i], oy[i], ox[i + 1], oy[i + 1], :blue)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x, y, "A:(x,y) ", :blue, :right, :vcenter)
       point(x0, y0, " B:(x0,y0)", :blue, :left, :vcenter)
       point(x1, y1, "等円:r1\n(x1,y1)", :red, :center, :bottom, delta=delta)
       point(0, R, " R:(0,R)", :black, :left, :bottom, delta=delta)
       point(r, 0, " r", :gray50, :left, :bottom, delta=delta)
   end
end;