算額（その804）

算額（その804）

藤田貞資：精要算法（下巻），天明元年(1781)
http://www.wasan.jp/seiyou/seiyou.html

長方形内に甲，乙，丙，丁の 4 円を入れる。甲円の直径が 5140 寸のとき，乙円の直径はいかほどか。

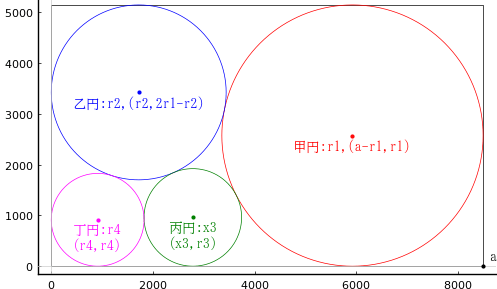
甲円の半径と中心座標を r1, (a - r1, r1)
乙円の半径と中心座標を r2, (r2, 2r1 - r2)
丙円の半径と中心座標を r3, (x3, r3)
丁円の半径と中心座標を r4, (r4, r4)
長方形の長辺を a とおく。短辺は 2r1 である。
以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, r1::positive, r2::positive, r3::positive, x3::positive, r4::positive
eq1 = (a - r1 - r2)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = (a - r1 - x3)^2 + (r1 - r3)^2 - (r1 + r3)^2
eq3 = (x3 - r2)^2 + (2r1 - r2 - r3)^2 - (r2 + r3)^2
eq4 = (r2 - r4)^2 + (2r1 - r2 - r4)^2 - (r2 + r4)^2
eq5 = (x3 - r4)^2 + (r3 - r4)^2 - (r3 + r4)^2
res = solve([eq1, eq2, eq3, eq4, eq5], (a, r2, r3, x3, r4));
res[3]

   (r1*(3*sqrt(28*sqrt(2) + 185) + 34*sqrt(2) + 8*sqrt(56*sqrt(2) + 370) + 187)/136, r1*(-43*sqrt(28*sqrt(2) + 185) - 187 + 10*sqrt(56*sqrt(2) + 370) + 272*sqrt(2))/(68*(-sqrt(28*sqrt(2) + 185) + 2*sqrt(2) + 7)), r1*(-19*sqrt(28*sqrt(2) + 185) - 68*sqrt(2) + 6*sqrt(56*sqrt(2) + 370) + 221)/(17*(-sqrt(28*sqrt(2) + 185) + 2*sqrt(2) + 7)), r1*(-58*sqrt(56*sqrt(2) + 370) - 391 + 25*sqrt(28*sqrt(2) + 185) + 612*sqrt(2))/(68*(-sqrt(28*sqrt(2) + 185) + 2*sqrt(2) + 7)), r1*(-sqrt(7*sqrt(2)/16 + 185/64) + sqrt(2)/4 + 15/8))

4 組の解が得られるが，3 番目のものが適解である。

乙円の直径は，t = √(28√2 + 185) とおくと，甲円の直径の ((7 - 4√2)t + 119 - 34√2)/136 倍である。

甲円の直径が 5140 寸のとき，乙円の直径は 3441.0001373070395 寸である。

「答」では「三千四百四十寸◯◯◯有奇」とあるが，誤記であろう。

t = √(28√2 + 185)
5140*((7 - 4√2)t + 119 - 34√2)/136

   3441.0001373070395

その他のパラメータは以下のとおりである。

a = 8496.06;  r2 = 1720.5;  r3 = 959.736;  x3 = 2785.03;  r4 = 912.939

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 5140//2
   t = sqrt(28*sqrt(2) + 185)
   u = 2√2 + 7 - t
   (a, r2, r3, x3, r4) = r1 .* (
       (3*t + 8*√2t + 187 + 34√2)/136,
       (-43*t + 10*√2t - 187 + 272√2)/68u,
       (-19*t + 6*√2t + 221 - 68√2)/17u,
       (25*t -58*√2t - 391 + 612√2)/68u,
       (-sqrt(7√2/16 + 185/64) + √2/4 + 15/8))
   @printf("乙円の直径 = %g\n", 2r2)
   @printf("a = %g;  r2 = %g;  r3 = %g;  x3 = %g;  r4 = %g\n", a, r2, r3, x3, r4)
   plot([0, a, a, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5)
   circle(a - r1, r1, r1)
   circle(r2, 2r1 - r2, r2, :blue)
   circle(x3, r3, r3, :green)
   circle(r4, r4, r4, :magenta)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a - r1, r1, "甲円:r1,(a-r1,r1)", :red, :center, delta=-delta)
       point(r2, 2r1 - r2, "乙円:r2,(r2,2r1-r2)", :blue, :center, delta=-delta)
       point(x3, r3, "丙円:x3\n(x3,r3)", :green, :center, delta=-delta)
       point(r4, r4, "丁円:r4\n(r4,r4)", :magenta, :center, delta=-delta)
       point(a, 0, " a", :black, :left, :bottom, delta=delta)
   end
end;