算額（その1340）

算額（その1340）

岐阜県垂井町 西法寺 令和6年(2024)
http://www.wasan.jp/gifu/saihoji.html
算法点竄指南録　七十一
https://kokusho.nijl.ac.jp/biblio/100301503/38?ln=ja

キーワード：楕円，直角三角形
#Julia, #SymPy, #算額, #和算

直角三角形の中に楕円を容れる。股が 8 寸，長径が 4 寸，短径が 2 寸のとき，鈎はいかほどか。

求める鈎を「鈎」とする。
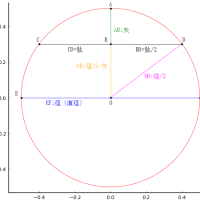
図の横幅を 1/2 に縮小する（高さはそのまま）と，楕円は直径 2 寸の円になり，股は 4 寸になる。
直角三角形に内接する円の直径を d とすると，
鈎 + 股 - sqrt(鈎^2 + 股^2) = d の関係がある。
この方程式を「鈎」について解けばよい。

include("julia-source.txt");

using SymPy
@syms 鈎::positive, 股::positive, d::positive;
eq1 = 鈎 + 股 - sqrt(鈎^2 + 股^2) - d
res = solve(eq1, 鈎)[1]
res |> println

   d*(d - 2*股)/(2*(d - 股))

鈎 = d*(d - 2*股)/(2*(d - 股)) において，d = 2, 股 = 4 を代入すれば，鈎 = 3 が得られる。

res(d => 2, 股 => 4) |> println

   3

function draw(股, 長径, 短径)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   d = 短径
   factor = 短径/長径
   鈎 = d*(d - 2*股*factor)/(2*(d - 股*factor))
   plot([0, 股, 股, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
   ellipse(股 - 長径/2, 短径/2, 長径/2, 短径/2, color=:blue)
   plot!([股 - 股*factor, 股, 股, 股 - 股*factor], [0, 0, 鈎, 0], color=:red, lw=0.5)
   circle(股 - d/2, d/2, d/2, :red)
end;

draw(8, 4, 2)