算額（その1338）

算額（その1338）

[電子復刻 『和算家　北明 寺島宗伴』]
http://www.wasan.jp/
算法天元算題花 三遍下
http://www.wasan.jp/terasima/terasima3.pdf

キーワード：直角三角形，重心
#Julia, #SymPy, #算額, #和算

重さが 6 キログラムの直角三角形 ABC（∠ABC = 90°）の形の板がある。
底辺 BC が水平になるように B と C の位置で真上に平行に持ち上げる。このとき，B，C にはどれだけの力が必要か。

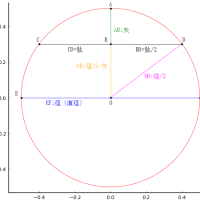
B を原点 (0, 0) とする。A, C の座標を (0, AB), (BC, 0) とする。
重心の座標 (x, y) は，AB の中点 (0, AB/2) と (BC, 0) を結ぶ線分と，(AB/2, BC/2) と原点 (0, 0) を結ぶ線分の交点である。
(x, y) = (BC/3, AB/3) となる。
重心から BC に垂線をおろしたとき，垂線の脚を D とすると，BD:CD = 1:2 である。

直角三角形の重さ w は，重心から下向きのベクトル，B(0, 0)，C(c, 0) で持ち上げる上向きのベクトルを f1, f2 とすると以下の連立方程式が成り立つ。

include("julia-source.txt");

using SymPy
@syms AB::positive, BC::positive, BD::positive, CD::positive,
     w::positive, f1::positive, f2::positive;
(x, y) = intersection(0, AB/2, BC, 0, 0, 0, BC/2, AB/2)

   (BC/3, AB/3)

CD = 2BD
eq1 = (f1 + f2) - w
eq2 = BD*f1 - CD*f2
res = solve([eq1, eq2], (f1, f2));
res[f1], res[f2]

   (2*w/3, w/3)

(res[f1](w => 6), res[f2](w => 6))

   (4, 2)

B，C に必要な力は 4 キログラム，2 キログラムである。

function draw(AB, BC, more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x, y) = (BC/3, AB/3)
   plot([0, BC, 0, 0], [0, 0, AB, 0], color=:blue, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x, y, "重心 (x,y)", :blue, :center, :bottom, delta=delta)
       point(0, AB, " A", :blue, :left, :bottom, delta=delta)
       point(0, 0, " B", :blue, :left, :bottom, delta=delta)
       point(BC, 0, " C", :blue, :left, :bottom, delta=delta)
       point(x, 0, " D", :blue, :left, :bottom, delta=delta)
       plot!([0, 0], [0, 2AB/3], arrow=:arrow, color=:red, lw=1.5)
       plot!([BC, BC], [0, AB/3], arrow=:arrow, color=:red, lw=1.5)
       plot!([x, x], [y, y - AB], arrow=:arrow, color=:green, lw=1.5)
   end  
end;

draw(3, 6, true)