前回の問題
1つの円周上に、等間隔に並んだ点が
N個あります。
このN個の点を結ぶ線を書いたとき、その線の数は276本になりました。
点の数は いくらだったのでしょうか?
この中で、大問題なのが 対角線の数をどうやって求めるのか?
ということでしょうか・・・
正多角形の場合、対角線はある点から別の点に向かって引きますが
そのとき自分自身と、自分の両隣の点には引けません
たとえば、正六角形の場合だと、1つの点から引ける対角線は
6-3で、3本! これが6カ所あるので
3×6 で18本! いや待てよ?
この数え方だと、1本の対角線を2回数えてしまいますから
18÷2 で9本。 これを実際に描いた図で確認しますと
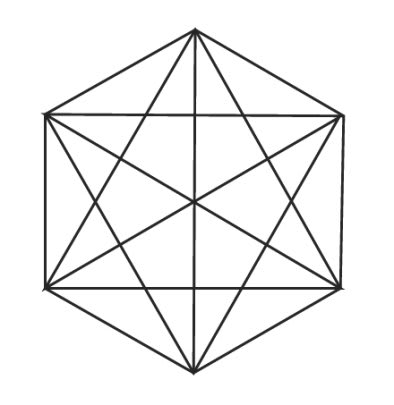
あってる!(当たり前なのですが・・・)
N角形だと、対角線の数は
(N-3)×N÷2 で 計算できます。
問題の、線の数は この対角線と外側の辺の数の合計が276ですから
N(N-3)÷2+N=276 この式を解けば Nが 点の数と分かります。
式を整理して
2×(N(N-3)÷2+N)=2×276
N×N-N-552=0
因数分解して、(552を素数の積にするとわかりやすいかも)
*552=2×2×2×3×23=24×23
(N+23)(N-24)=0
N=-23 は 使えないので
N= 24 点の数は 24個
この問題は、因数分解を使いますので、中学3年生向けですが
たとえば正12角形の対角線の数を求めましょう という問題なら、
小学生でも 解けます!