どもども。こんにちは。
前回は今年の東大理系数学の第1問を取り上げてみました~
そこで今回は第2問を取り上げてみたいと思います
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon2.html
確率の問題ですね

9つの部屋があって,1秒ごとに辺を共有する隣の部屋に移動するというものです。
ではとりあえず図にあるように9つの部屋にA,B,C,D,E,F,P,Q,Rと名前を付けてしまいましょう。
Pがスタート地点。n秒後にQにいる確率が求めたいものです。
この手の問題は確率漸化式を立ててそれを解く,という解法が
とても有効です
というわけで,とりあえず何も考えずにn秒後にA,B,C,D,E,F,P,Q,Rにいる確率をそれぞれ
a_n,b_n,c_n,d_n,e_n,f_n,p_n,q_n,r_nとおきましょう
ワーイ,めんどくせー
9つも数列があったらやる気が失せますね♪
でもまぁ実際やってみると,実はそんなに大変でもなかったりするんですが。
図形の対称性を使うと,数列の数を減らせます。
例えばn秒後にQにいる確率とRにいる確率は等しくなります。
同様にBとC,EとFにいる確率はそれぞれ等しいです。
そんなわけで,とりあえず何も考えずに9つの数列を考えた場合の解法を挙げてみます。
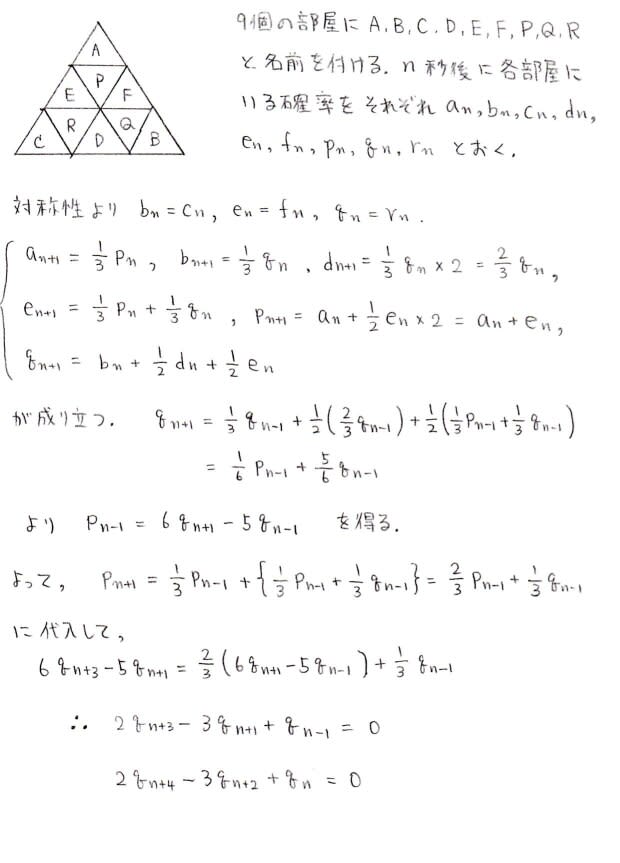
たくさんあった数列たちを消去しまくってq_nだけの漸化式を得ました。
3項間漸化式ぽい形が出てきましたね
出てくる項が1つおきになってるので,q_nの奇数番目の項を並べた数列 q_{2m-1} (m≧1) と偶数番目を並べた数列 q_{2m} (m≧1) に関しては
隣接3項間漸化式になっております。
特に奇数番目に注目してみると,
q_1=q_3=0 から順にq_5=q_7=q_11=……=0が得られます。
簡単な実験で分かることですが,球は奇数秒後には常にP,Q,R以外の部屋にあり,偶数秒後にはP,Q,Rのいずれかに入っています
実質的に偶数秒後の球の位置を考えればよいわけですね!
さて,与えられた3項間漸化式ですが,一般に a_{n+2}+Aa_{n+1}+Ba_{n}=0 において 1+A+B=0 のときは扱い方が比較的に楽チンでして,
a_{n+2}-a_{n+1}=B(a_{n+1}-a_{n})
及び a_{n+2}-Ba_{n+1}=a_{n+1}-Ba_{n}
が成り立つので計算がし易いです。

というわけで,答えが得られたのでめでたしめでたしです~。
では,今回も別解法を考えてみます。
上記のやり方では,何も考えずに9つの数列を用意しました。
でも,それをする前にちょこっと実験してみて,奇数秒後に確率は常に0で
偶数秒後には常にP,Q,Rにしか居ないということに気付いてしまえば,
わざわざ9つも数列を考える必要はなくって,p_n,q_n,r_nの3つで十分だったという事が分かるかと思います。しかも対称性から q_n=r_n なので,
実質的には2つの数列で事足ります。

先程よりもスッキリした解法が得られました。今度は3項間漸化式も使っていません。
ここからは敢えて面倒なことをしてみる事にしましょう。
今の解法で出てきた q_{2m}=1/6+(1/2)q_{2(m-1)} という2項間漸化式。
これは q_{n+2}=1/6+(1/2)q_{n},q_1=(任意),q_2=1/6 で与えられた
3項間漸化式という見方も出来ますね。
これを解く上では,q_1は任意の値で支障はありません。ただし,この漸化式で奇数秒後にQにいる確率を得ることは出来ません。実際,q_1=0としたとき
q_3=1/6が出てきてしまい,q_3=0は出てきません。
その理由は,漸化式を得る過程で全確率 p_n+q_n+r_n=1 という関係式を
用いているからであります。この関係式は偶数秒後でしか成り立ちません。
そんなこんなで,わざわざ3項間漸化式を解いて答えを得てみましょう。

随分と面倒くさい式が出てきましたね
最後に,もっと面倒くさい解法を1つ与えて終わりにしましょう。
0秒後,2秒後,4秒後,……,2m秒後の球のいる部屋を順に書き下すと
PPPQQPQRRQのような,P,Q,Rの重複順列が出現します。
PからスタートしてQで終わるような順列の数を利用して答えの確率を
求めてみようという,なかなか面倒なやり方です

最終的には2項定理まで出てきます。


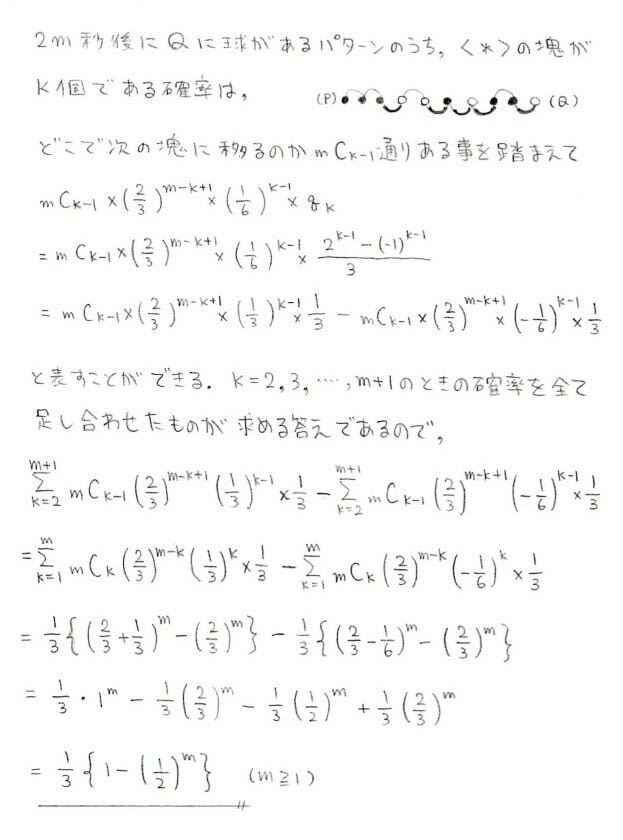
前回は今年の東大理系数学の第1問を取り上げてみました~
そこで今回は第2問を取り上げてみたいと思います

問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon2.html
確率の問題ですね


9つの部屋があって,1秒ごとに辺を共有する隣の部屋に移動するというものです。
ではとりあえず図にあるように9つの部屋にA,B,C,D,E,F,P,Q,Rと名前を付けてしまいましょう。
Pがスタート地点。n秒後にQにいる確率が求めたいものです。
この手の問題は確率漸化式を立ててそれを解く,という解法が
とても有効です

というわけで,とりあえず何も考えずにn秒後にA,B,C,D,E,F,P,Q,Rにいる確率をそれぞれ
a_n,b_n,c_n,d_n,e_n,f_n,p_n,q_n,r_nとおきましょう

ワーイ,めんどくせー

9つも数列があったらやる気が失せますね♪
でもまぁ実際やってみると,実はそんなに大変でもなかったりするんですが。
図形の対称性を使うと,数列の数を減らせます。
例えばn秒後にQにいる確率とRにいる確率は等しくなります。
同様にBとC,EとFにいる確率はそれぞれ等しいです。
そんなわけで,とりあえず何も考えずに9つの数列を考えた場合の解法を挙げてみます。
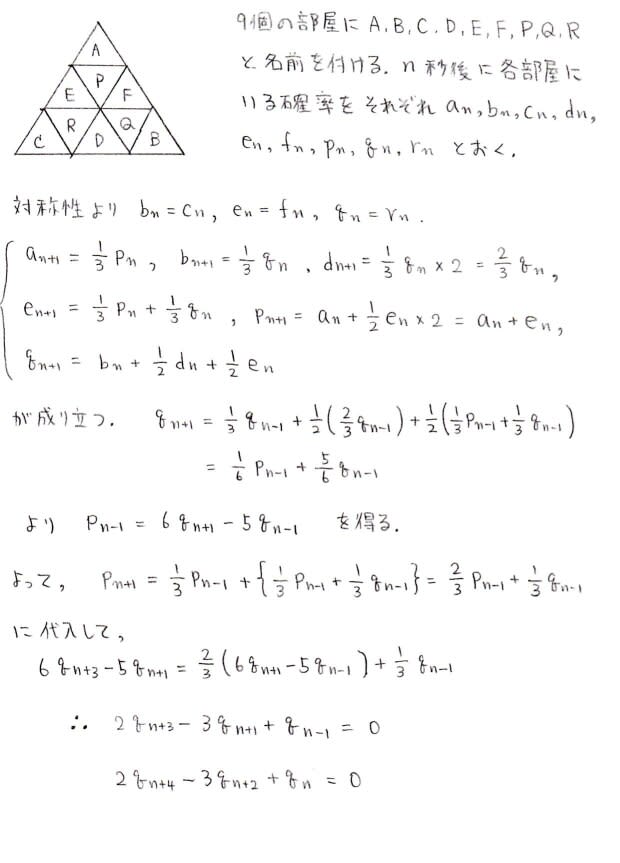
たくさんあった数列たちを消去しまくってq_nだけの漸化式を得ました。
3項間漸化式ぽい形が出てきましたね

出てくる項が1つおきになってるので,q_nの奇数番目の項を並べた数列 q_{2m-1} (m≧1) と偶数番目を並べた数列 q_{2m} (m≧1) に関しては
隣接3項間漸化式になっております。
特に奇数番目に注目してみると,
q_1=q_3=0 から順にq_5=q_7=q_11=……=0が得られます。
簡単な実験で分かることですが,球は奇数秒後には常にP,Q,R以外の部屋にあり,偶数秒後にはP,Q,Rのいずれかに入っています

実質的に偶数秒後の球の位置を考えればよいわけですね!
さて,与えられた3項間漸化式ですが,一般に a_{n+2}+Aa_{n+1}+Ba_{n}=0 において 1+A+B=0 のときは扱い方が比較的に楽チンでして,
a_{n+2}-a_{n+1}=B(a_{n+1}-a_{n})
及び a_{n+2}-Ba_{n+1}=a_{n+1}-Ba_{n}
が成り立つので計算がし易いです。

というわけで,答えが得られたのでめでたしめでたしです~。
では,今回も別解法を考えてみます。
上記のやり方では,何も考えずに9つの数列を用意しました。
でも,それをする前にちょこっと実験してみて,奇数秒後に確率は常に0で
偶数秒後には常にP,Q,Rにしか居ないということに気付いてしまえば,
わざわざ9つも数列を考える必要はなくって,p_n,q_n,r_nの3つで十分だったという事が分かるかと思います。しかも対称性から q_n=r_n なので,
実質的には2つの数列で事足ります。

先程よりもスッキリした解法が得られました。今度は3項間漸化式も使っていません。
ここからは敢えて面倒なことをしてみる事にしましょう。
今の解法で出てきた q_{2m}=1/6+(1/2)q_{2(m-1)} という2項間漸化式。
これは q_{n+2}=1/6+(1/2)q_{n},q_1=(任意),q_2=1/6 で与えられた
3項間漸化式という見方も出来ますね。
これを解く上では,q_1は任意の値で支障はありません。ただし,この漸化式で奇数秒後にQにいる確率を得ることは出来ません。実際,q_1=0としたとき
q_3=1/6が出てきてしまい,q_3=0は出てきません。
その理由は,漸化式を得る過程で全確率 p_n+q_n+r_n=1 という関係式を
用いているからであります。この関係式は偶数秒後でしか成り立ちません。
そんなこんなで,わざわざ3項間漸化式を解いて答えを得てみましょう。

随分と面倒くさい式が出てきましたね

最後に,もっと面倒くさい解法を1つ与えて終わりにしましょう。
0秒後,2秒後,4秒後,……,2m秒後の球のいる部屋を順に書き下すと
PPPQQPQRRQのような,P,Q,Rの重複順列が出現します。
PからスタートしてQで終わるような順列の数を利用して答えの確率を
求めてみようという,なかなか面倒なやり方です


最終的には2項定理まで出てきます。


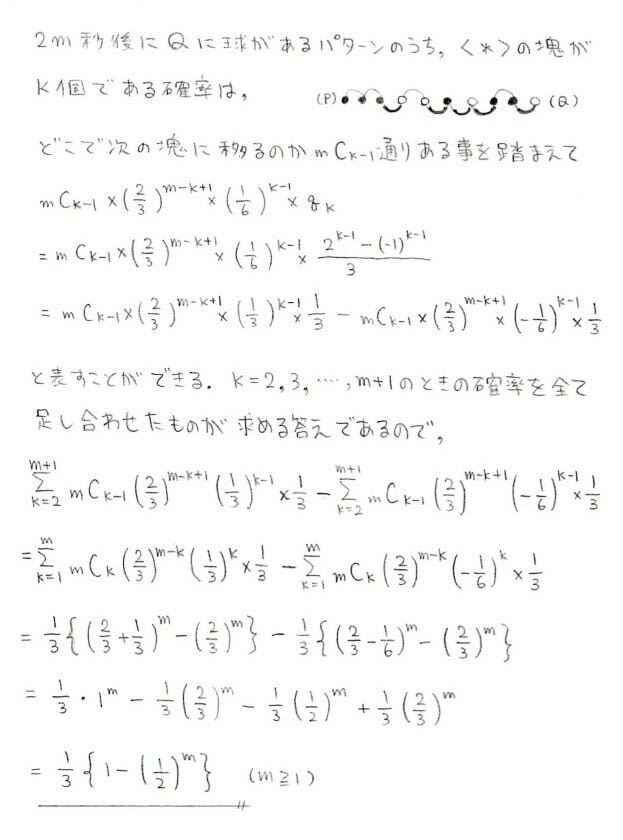















※コメント投稿者のブログIDはブログ作成者のみに通知されます