①振り返ってみると 小学生、中学生、高校生などに 統計の学びも 遅まきながら 文部省が近年になってPC進化などありて「学習指導要領の改正」等の統計を学ぶ環境整備が行われています。
②すでに社会人として活躍している人達の生涯教育にむけても「統計ブーム」となっていて参考図書は沢山販売されています。
③学ぶ者である私の体験から 学びの 入口を発掘するのに 大変迷走しました、幸いに「文部科学省認定社会通信講座(実務教育研究所)にたどり着き随分助かりました。
今回の日記は パソコンの進化によって 学ぶ人たちに支援をしてくれている仕組みをご紹介しようと思い投稿しました。
下記別紙を御覧ください 現在のWindows7・10には統計を簡単に分析できる「分析ツール」も用意されています。
それに加えて「Excel関数」という便利な簡易な計算はできるように機能アップしています。
今回の日記は 分析ツールを使って実体験を行ってみてほしいです。ここでは「猿まね」をお勧めします。頑張ってほしいものですね。


以上です。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
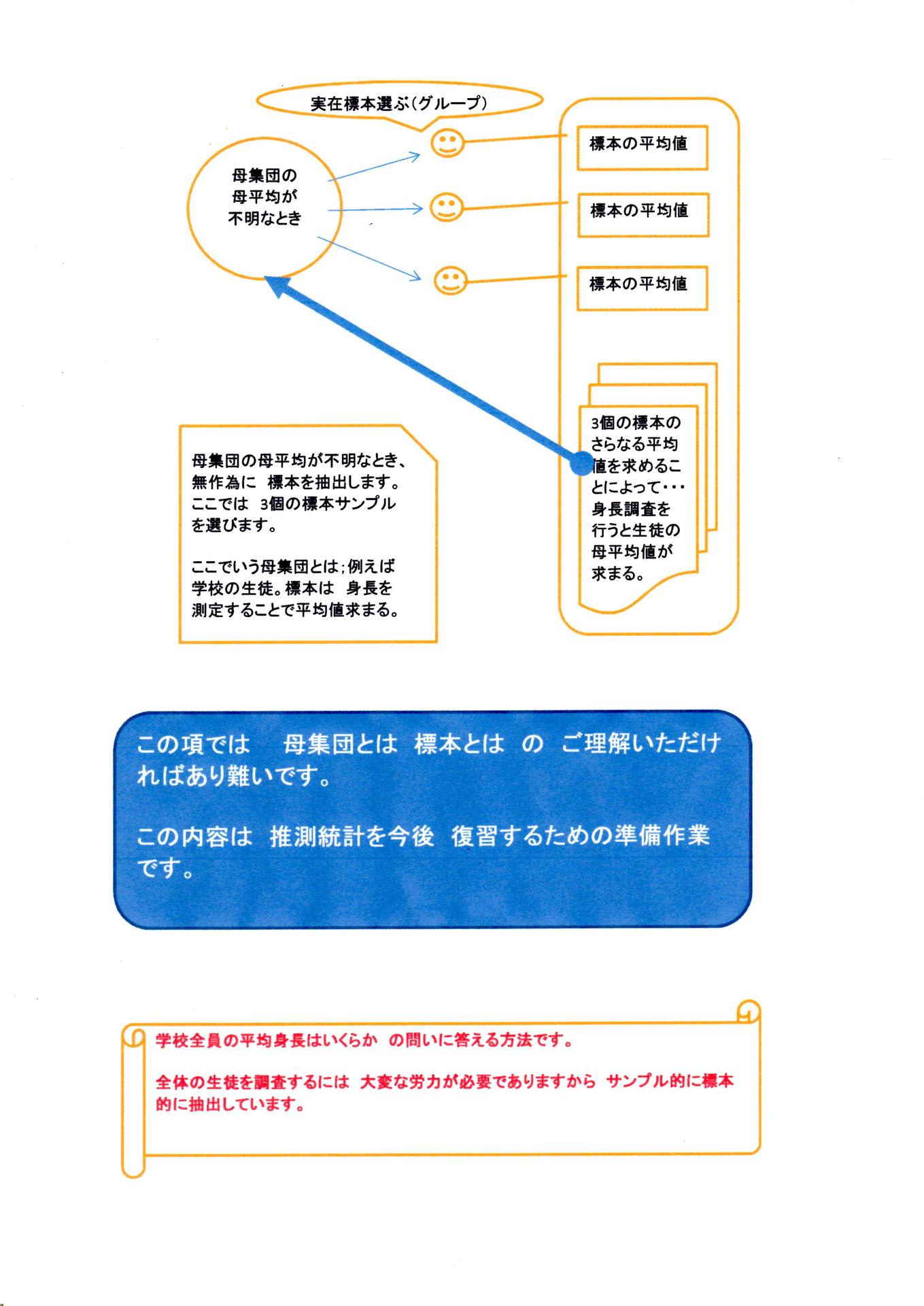
母集団と 標本の 関係は 概念的に 次のようになっている。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
では より 具体的には 現存値 つまり 200件のデータを使って 実験してみよう。母平均は142CMが正解です

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
標本から 得られる 母集団の 実態に 迫るには 標本調査は 幾らが妥当なのでしょう、 いや無理であれば 確率変数を告げることで信頼してもらえるのではないでしょうか。確率変数;X(エックス) → 期待値;E(Expeccted) → 分散値;V(Variance)と統計学では言うそうです。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

統計の猿より投稿
①ここでいう母集団とは 未知の全数観測対象物である。
②また標本とは・・・母集団に関する情報に導くデータ分析の媒体である。標本観測または標本調査を実施して母集団値に到達する。
と思います。
では 標本介して 母集団に到達する経過をご覧ください。

・・・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・・・
分析結果をご覧になって 実在母集団 と 標本分析結果と 一致しない時がある。一致しない説明は「確率変数」で説明できるという、つまり「二項分布」のことだ。私(統計の猿)は勉強不足である****ごめんなさい***
推測統計は 教本学習中は 苦手の 分析でした.
昨年1年間は 記述統計 と言い データが持つ情報を要約して 可視化などわかりやすするための記述統計のツールでした。
今回は 氷山の一角の標本を分析することで 全体像を解明する方法です。
教本の初めに「尺取り虫」を例にとり、過去の実績から 将来を予測するという方法です
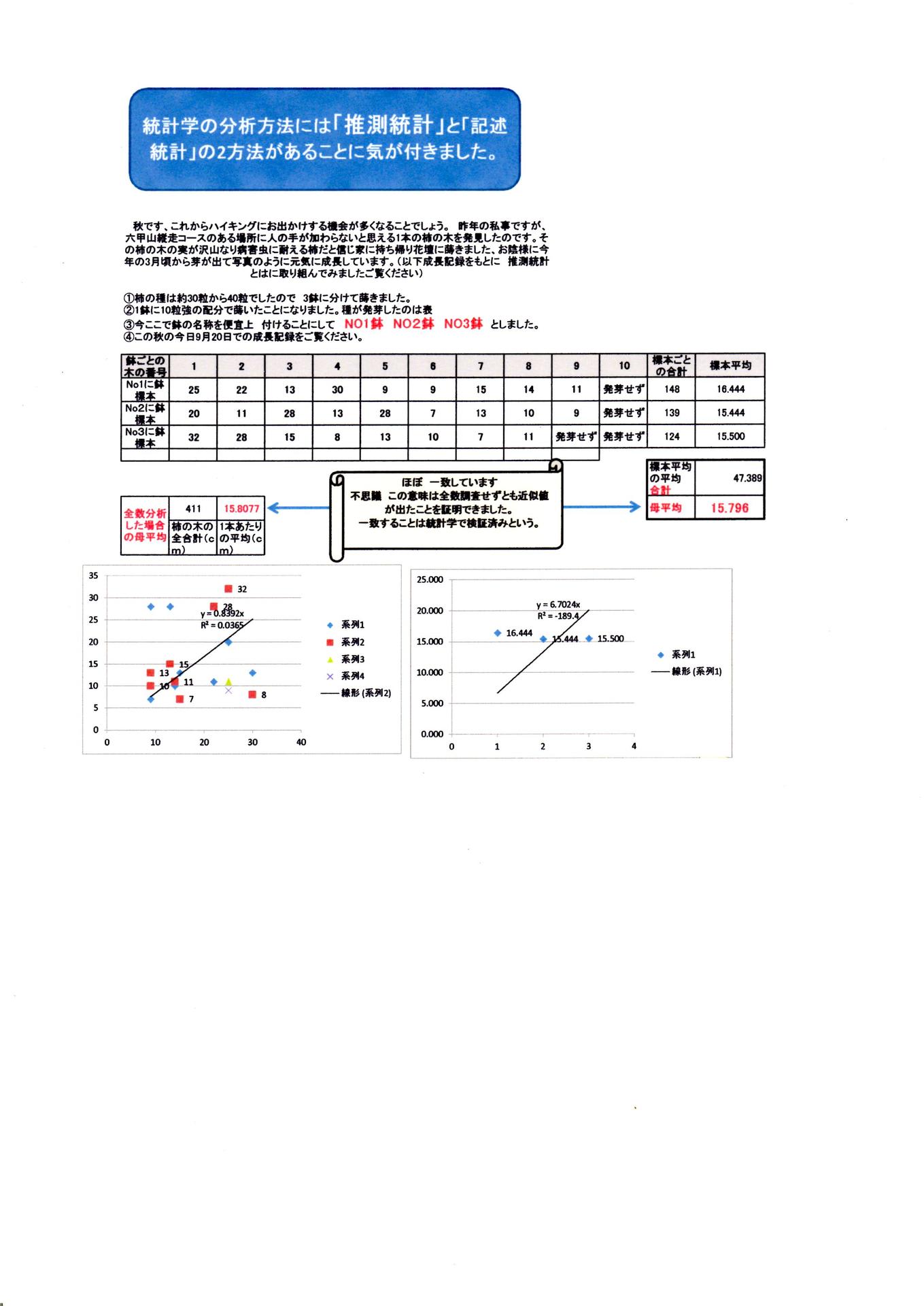
今回は 柿の種を栽培した記録を 活用して「推測統計」を復習してみました。記録の単位は 柿の芽の高さ(単位は cm )母平均値は15cmです。
まず写真をご覧ください。この写真は種まき後6か月経過し柿の成長状態です。

母集団を発掘してみました

サンプル標本平均の・平均値は母平均となります 分析概念表です

以上。

統計分析にサンプルとしている場所は 岡山県北西部の小中学生の生徒数である。中学校は1校で十分あるという。残る人は高齢者ばかりだ。(関数を使って、で中学3年間の移動平均法で出してみよう 3年後は何人?)
また 地方創生プログラム 5ケ年計画を添付しておきました。 読者の感想はいかがでしょう。
①別紙A;小学校中学校の生徒数の減少に歯止めがかかりません
別紙B;東京一極集中対策は、どのようになるのでしょうか、文化庁は京都、統計局は和歌山等 次の打つ手は何でしょうね 以上。
 ・・・
・・・
統計との出会いから 今日までの取り組みは、大きな出会いでした。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
現代統計実務講座の内容です。 別紙の中で特に「ページ数」にこだわりレポート1回あたりの資質を推測下されば、さすが内容が 文部省認定教本 だけあることがお分かりになるでしょう。
別紙の中で特に「ページ数」にこだわりレポート1回あたりの資質を推測下されば、さすが内容が 文部省認定教本 だけあることがお分かりになるでしょう。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
以下2ページには、ブログを通じて、学びを日記風に42件公開しました ・・
・・


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
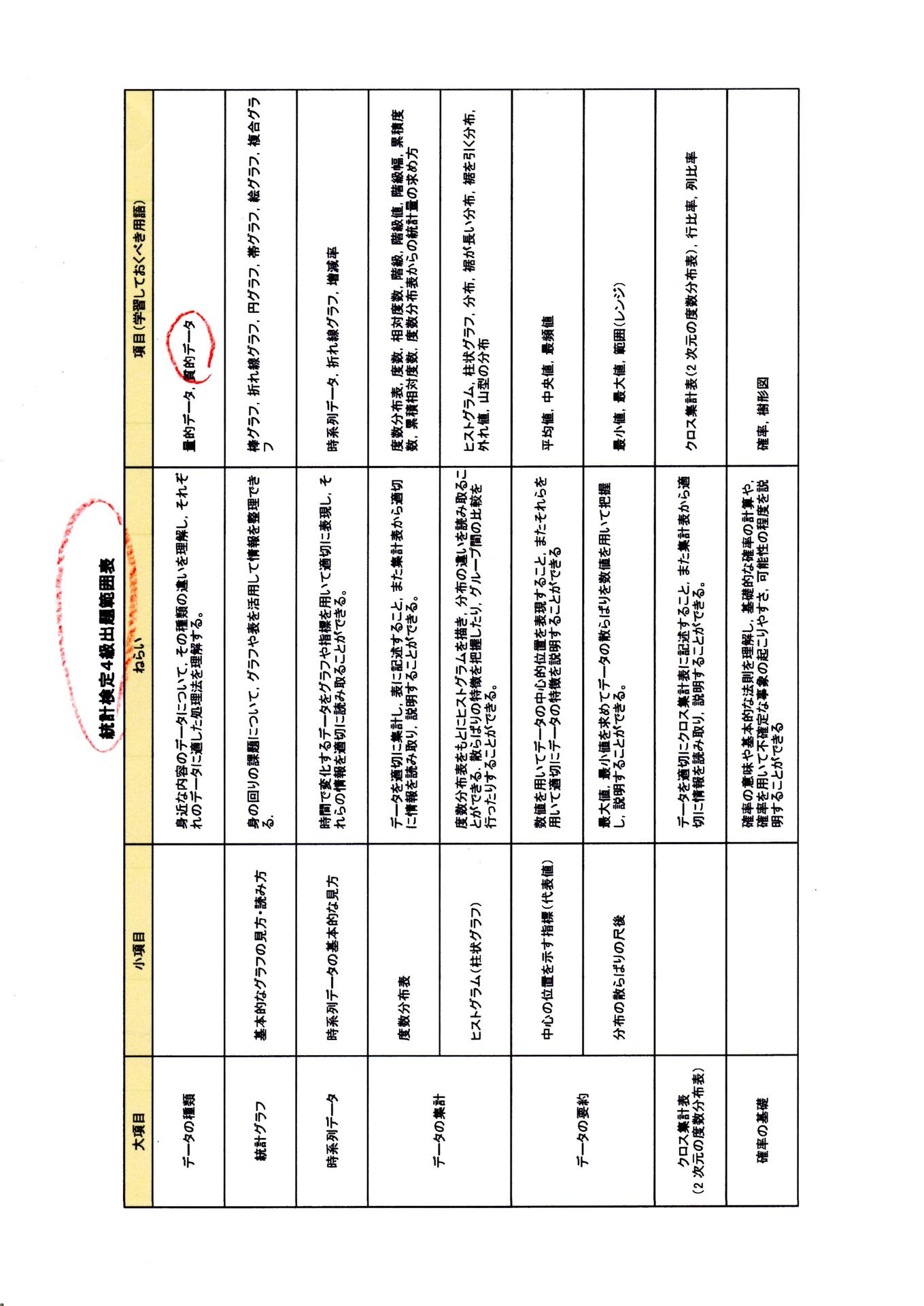
前のレポート42件を作成に当たり「統計検定出題範囲・検定4級程度内容」です 赤鉛筆で丸を書いた箇所以外は取り組んでいません。
赤鉛筆で丸を書いた箇所以外は取り組んでいません。
 以上。
以上。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
こんにちわ 日ごろ私の(統計の猿)のブログ訪問くださいまして ありがとうございます。
ブログの機能については、ご存知の通りブログ作成者の人気度ランキングが確認できるシステムになっています。投稿原稿を作成に当たり一番気になるところです。
最近の1週間で合計で150名平均ですつまり1日当たり20名の訪問者があり、あの小難しい「回帰分析」の原稿をお読みに来てくださる読者様には敬意を表すところです。
過去に、道路の実測調査を投稿すると1日で数百名の閲覧者がある一方で、難易度を上げると1日平均20名程度です。私は悲しく感じるよりか逆に義務教育に、やっと統計学が導入されたばかりのこの世相で、関心をお持ちの読者様がいらしゃると思いうれしく思っているのです。
では表題の「統計検定4級合格 最年少の声をご紹介します」
今日の私の日記は「日本最小年齢者の統計検定4級合格」取得情報をお伝えするわけですが、私事の昨日の「新聞切り抜き」の人気ランキング116名でした、これだけ社会が熟して統計に関心がおありと思いました。では以下をごらんください。
①小学校 5年生 が統計4級検定に合格した声をご紹介します。

②統計4級検定出題範囲です 小学生がこの範囲を統計4級試験に60点以上とれたとは素晴らしいですね。
小学生がこの範囲を統計4級試験に60点以上とれたとは素晴らしいですね。
③より詳しく知りたいお方は下記ホームページをご覧ください。
検索 http://www.toukei-kentei.jp/
以上。
すでに京都には 文化庁が移転する報道は読者様はすでにご存じと思いますが、新聞報道によると統計局が「和歌山に移転する」と発表がありました。

次の 関係ホームべージもあわせて御覧ください・・・・・・・http://www.soumu.go.jp/toukei_toukatsu/index/seido/stkankyo.htm
統計の制度は着々と整備されつつあります。これから 益々の「アマチユアーの統計家」が増えることをうれしく感じています。
http://www.soumu.go.jp/toukei_toukatsu/index/seido/2-5-1.htm 統計調査員制度のご案内。
統計家を目指す「統計の猿より」
近年データをもとに回帰分析の手計算部分を 省略でき PCプログラムで簡単に解決できるようになりました。
その前に見えない、ここでいうブラックボックスとは、どんな意味かご説明しましょう、例えば 円周率の3.14の根拠を知らず義務教育で使っていましたが(トンネルの中には高校で学ぶ)微分法で証明解読でき納得した経験がおありと思います。つまり答えは「出力されるがその経緯」がわからない事をここでは言っています。
あまり便利過ぎて本質が不明のままだと顧客から「なぜ」の質問があったときに対処するのに御説明が出来ません。ブラックボックスの疑問に挑戦して何故このように分析できるのかをより深めてみました。一例をご覧ください。
別紙1は 分析用のサンプルデータですが、回帰分析を実施してみたいと思っています。(7月29日のレポート表を再掲)
分析用のサンプルデータですが、回帰分析を実施してみたいと思っています。(7月29日のレポート表を再掲)
別紙2は サンプルデータでは数字の乱立ばかりですので 良く解りません よって まず目で確認出来るようにグラフで可視化してみました(このような可視化表現は中学校で教えられています)
サンプルデータでは数字の乱立ばかりですので 良く解りません よって まず目で確認出来るようにグラフで可視化してみました(このような可視化表現は中学校で教えられています)
別紙3は グラフの回帰直線に、周辺データを 近似曲線として表現出力してきました。ぼちぼち このグラフが使えるかどうか教えてくれたのです、検証してみましょう(決定係数R2=0.09で あまり採用したくありませ(R2=0.5以上を採用)のでパスすることにしました。でどうするの?「PCの分析ツールを操作して視点を変えて回帰分析を試みてみましょう」
グラフの回帰直線に、周辺データを 近似曲線として表現出力してきました。ぼちぼち このグラフが使えるかどうか教えてくれたのです、検証してみましょう(決定係数R2=0.09で あまり採用したくありませ(R2=0.5以上を採用)のでパスすることにしました。でどうするの?「PCの分析ツールを操作して視点を変えて回帰分析を試みてみましょう」
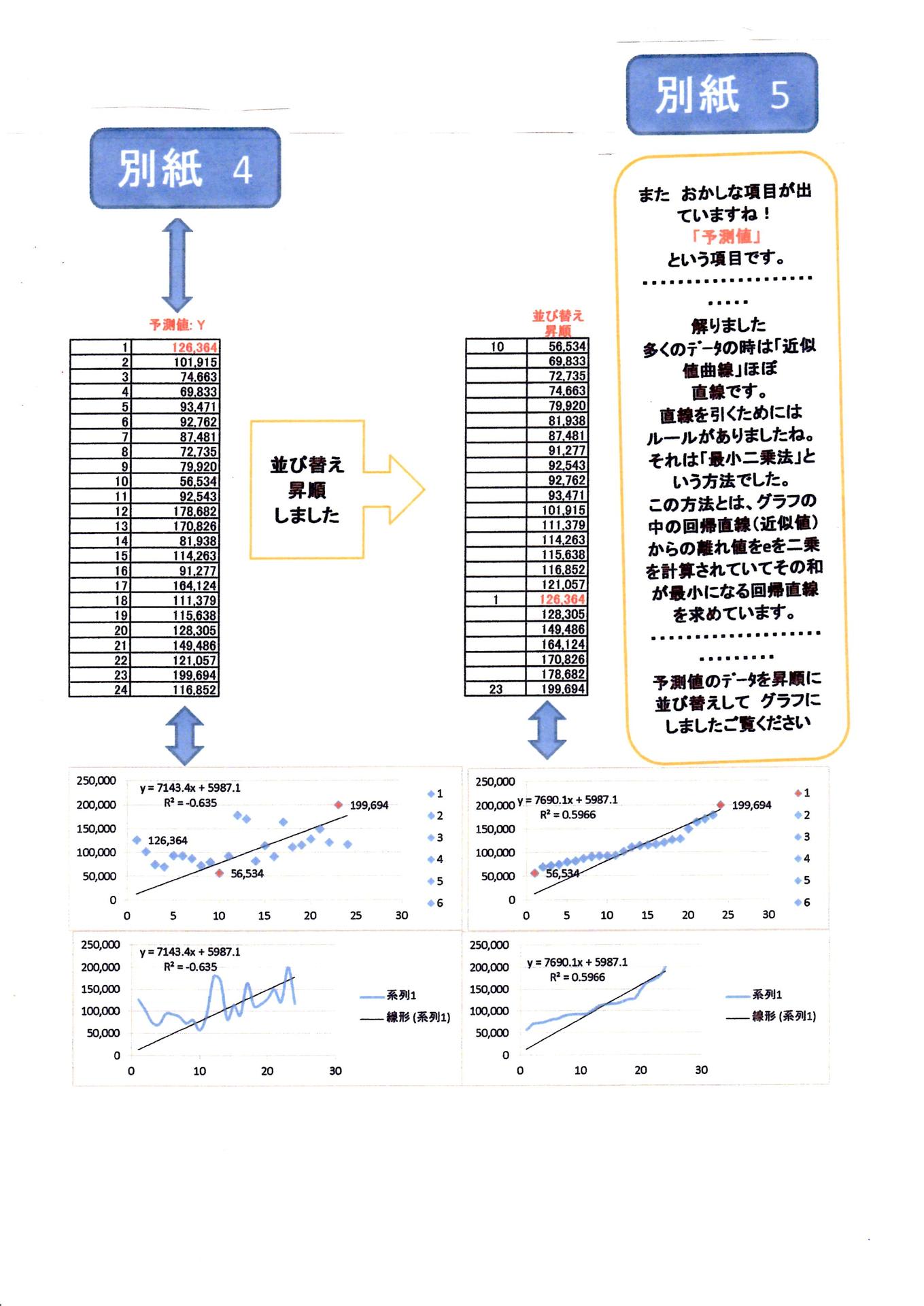
別紙4
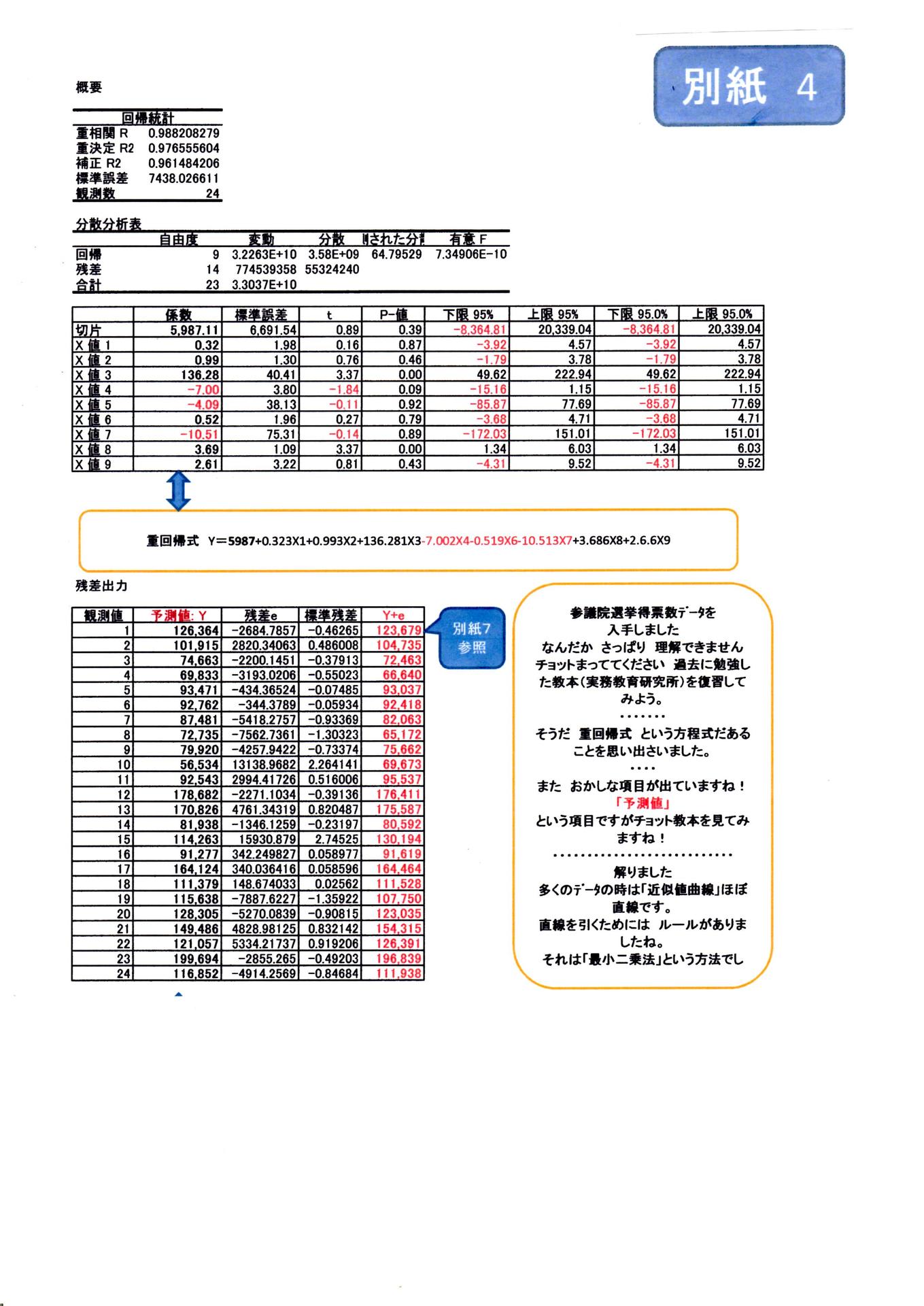
 最近は EXCEL 2010 以降のプログラムにて,ツールで分析できるようになりました、これが(トンネル)で直接 計算せずとも 分析してくれます。分析結果は別紙4が分析結果です。
最近は EXCEL 2010 以降のプログラムにて,ツールで分析できるようになりました、これが(トンネル)で直接 計算せずとも 分析してくれます。分析結果は別紙4が分析結果です。
しかし計算過程がブラックボックスに入って皆目わかりません、これでは 他のお人にご説明が出来ません(財団法人・実務教育研究所の教本で教えてくれます)。 例えば出た回答の中に「係数とは、切片とは、予測値とは、残差とは、P値とは、有意とは・せめて出力表の意味について教本復習しておきたいと思っています。
http://www.jitsumu.or.jp/index.php(財団法人・実務教育研究所の教本で教えてくれます)。
別紙5 予測値(Y=)の出力している「意味は回帰曲線の値でしたね」また 並べ変えるて昇順することで 連続性の点で表示しましたから、新たな発見に お気付くこととなりました。回帰曲線の決定係数はR2=0.5966ですから信頼できます。
予測値(Y=)の出力している「意味は回帰曲線の値でしたね」また 並べ変えるて昇順することで 連続性の点で表示しましたから、新たな発見に お気付くこととなりました。回帰曲線の決定係数はR2=0.5966ですから信頼できます。
別紙6 残差とは、どんな仕組みでしょうか、詳しく教えてくださる著書を発見しました、下記別紙をご覧ください、基本の勉強を後押しできる よい本です。
残差とは、どんな仕組みでしょうか、詳しく教えてくださる著書を発見しました、下記別紙をご覧ください、基本の勉強を後押しできる よい本です。
「係数とは、切片とは、予測値とは、残差とは、P値とは、有意とは・の疑問に答えてくださいます」(著者・日花弘子・EXCEL統計解析入門・2分冊別々販売中)
追伸 著書「高校生からの統計入門・加藤久和」の本は統計とは・・にこたえる教職員向けには易しすぎる内容です、私・統計の猿 にはちょうどよい著書では統計学の骨格の説明です、枝葉の部分には簡単に記述されています、私(統計の猿)は、学ぶ者の現在位置に活用しています。

別紙7 回帰関数を作成にあたり、2方法を試みてみました、①分析ツールから導き出す方法と②Exce関数・LINEST・から導き出す方法を見比べてみてください①=②とは一致しました。
回帰関数を作成にあたり、2方法を試みてみました、①分析ツールから導き出す方法と②Exce関数・LINEST・から導き出す方法を見比べてみてください①=②とは一致しました。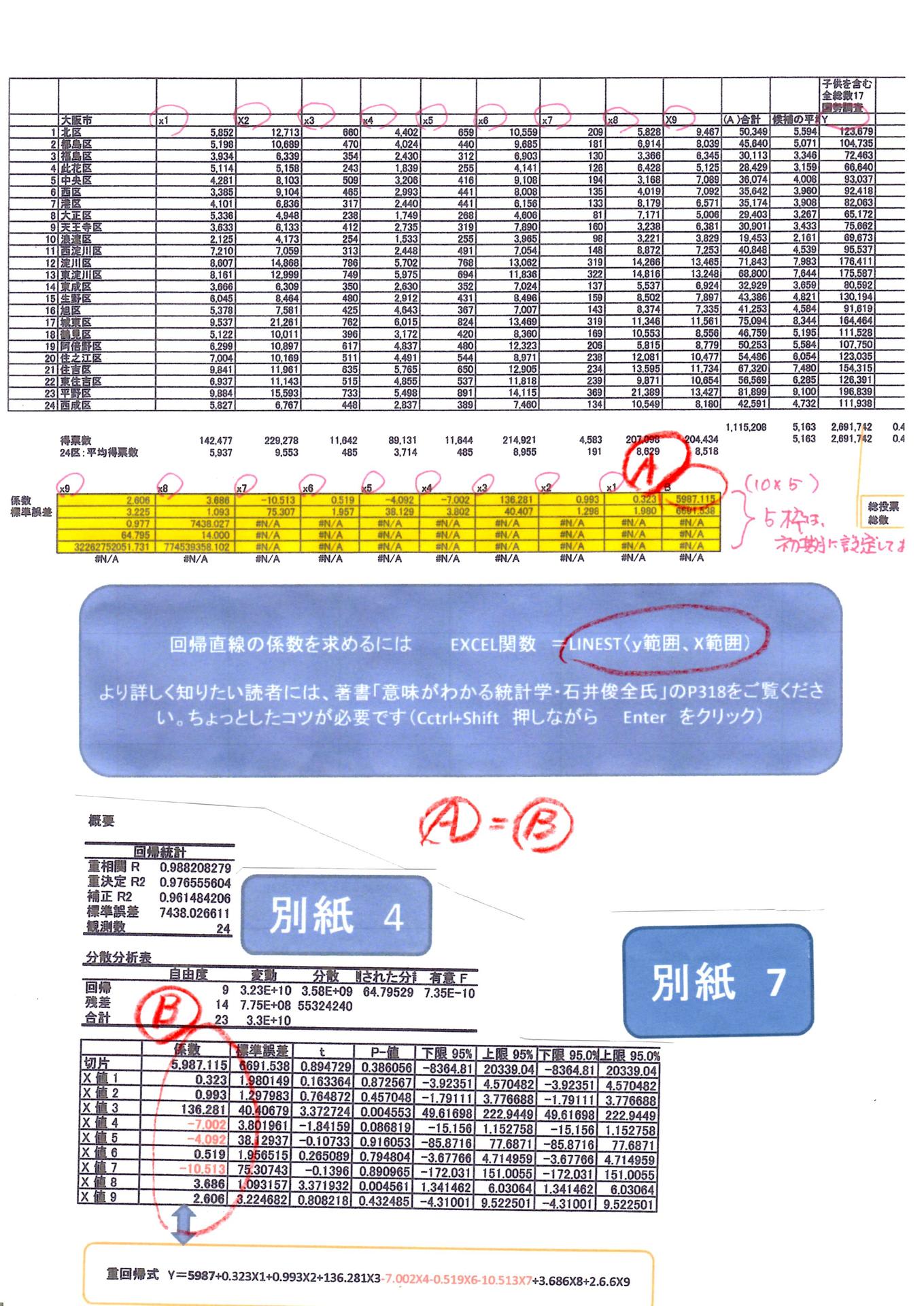
以上
選挙管理委員会が発表された ビックデータを利用して 独自の分析をしてみました。
ここでいう「独自」とは、①選挙投票者の家族構成が投票行動に変化が出ていないかを分析するものです。②極端な例でご説明しましょう、 5人のお子供を育てているお母さんの1票は 将来の準備として「高校入学に必要な無料化」をスローガンとした候補者の選挙公約に耳を傾けるのではないでしょうか。同じ1票であっても その家族構成での違いで無党派層の動向が違ってくるのでしょうか、気になります。
よって有権者は18歳以下であっても「その選挙区の投票権のない人も無視できない」と推測(仮説)を立ててみました,つまり 赤ちゃんから最高高齢者までが有権者という仮説をたてて「投票者の投票率」を計算してみました。
某区では 平均投票数41%の統計値の時に、ダミー値投票率が「27%」しか投票に参加していない選挙区を発見しました。①この選挙区の年齢構成がどのようになっているのでしょうか。②あるいは選挙権がないお子さんや外国のお方が多くいらしゃるのでしょうか??・・・わかりません。③あるいは民意が反映できず「待期児童」や「高齢者の介護」が遅れている事が気になりますね。
ご覧ください。

A・この表は 票投票権を持たない人を含む「政府の人口調査表」です。
票投票権を持たない人を含む「政府の人口調査表」です。


C・この表は A表の人口を「ダミー投票数」と呼んでします(統計学で使う特殊な操作です)。またこの表にはB表から抜粋した、候補者の得点数を合成した 分析表です。
A表の人口を「ダミー投票数」と呼んでします(統計学で使う特殊な操作です)。またこの表にはB表から抜粋した、候補者の得点数を合成した 分析表です。
日本の人口に等しい投票権があると 日本の国会はどのようなかじ取りになるでしょうね!政府が発表した日本の人口記録です。!http://www.stat.go.jp/data/nihon/02.htm


D・この表は 各候補者の得票実態の特徴を分析した一覧表です、例えばA候補者にあっては、ある選挙区では最小得票区では2125票 最大選挙区は9884票でした。というわけだ。
各候補者の得票実態の特徴を分析した一覧表です、例えばA候補者にあっては、ある選挙区では最小得票区では2125票 最大選挙区は9884票でした。というわけだ。


F・この表は 回帰分析といいますが さて読者で考えてみましょう。
回帰分析といいますが さて読者で考えてみましょう。

第24回参院選挙の議員さまが確定しました。統計学法の基本学習を使って 可視化しました。分析結果の候補者等及び所見は割愛させていただきます。またデータは大阪市選挙区の結果(比例は除く)を用いて分析してみました。統計表の平均値と標準偏差の関係学習すると「新たな発見が見えるのです」よって標準偏差とは何を表しているのか読者の方で解釈してみてください。選挙案件ですので感想は控えさせてください ごめんなさいね!!(標準偏差についてのご説明は・4月11日の私の日記を御覧ください 釣鐘状の正規分布でご説明させていただいています)
別紙Aは得票実績をサンプル使用しました。 左指で「Ctrl」キイを押さえながら右指で「P」を押し「Enter」タッチすることで「プリント印刷」ができます。
左指で「Ctrl」キイを押さえながら右指で「P」を押し「Enter」タッチすることで「プリント印刷」ができます。

別紙Bは選挙結果の特徴を表にしました。 左指で「Ctrl」キイを押さえながら右指で「P」を押し「Enter」タッチすることで「プリント印刷」ができます。
左指で「Ctrl」キイを押さえながら右指で「P」を押し「Enter」タッチすることで「プリント印刷」ができます。

別紙Cは相関関係分析をしてみました。 相関係数とは、サンプル値が直線であればサンプル数が2等分になり、サンプルが散らばっていると グラフの直線から左右に分散します。選挙の候補者にとっては ???????所見を見送りします。
相関係数とは、サンプル値が直線であればサンプル数が2等分になり、サンプルが散らばっていると グラフの直線から左右に分散します。選挙の候補者にとっては ???????所見を見送りします。

サンプルデータの中に 条件と一致するデータが 何個あるか調べたい。 その累計個数を 抽出する方法を確認しています・・・・事前に「B10:C14 」の表は作成しておくのがコツです。
ちょっと休憩・・・・ 政府の発表 ビッグ データ 御覧ください。
http://www.e-stat.go.jp/SG1/estat/eStatTopPortal.do
http://www.stat.go.jp/naruhodo/index.htm 統計学園へ