COUNTIF(範囲、参照）を利用して 混在ﾃﾞｰﾀから 個数を求めることが出来ます

今回の復習は事前に「A表」と「B表」を準備しました。

ここでいう「A表」とは、消防法によって実施義務がある項目である、部屋ごとに設置してある（火災感知器）の点検実績表です。

「B表]は、マンション管理員が行う　混在するﾃﾞｰﾀから　抽出して　整理整頓する　手順を　描写してあります。混在するごみの中から　私たちが知りたい　貴重な　ﾃﾞｰﾀを　発掘するのです。

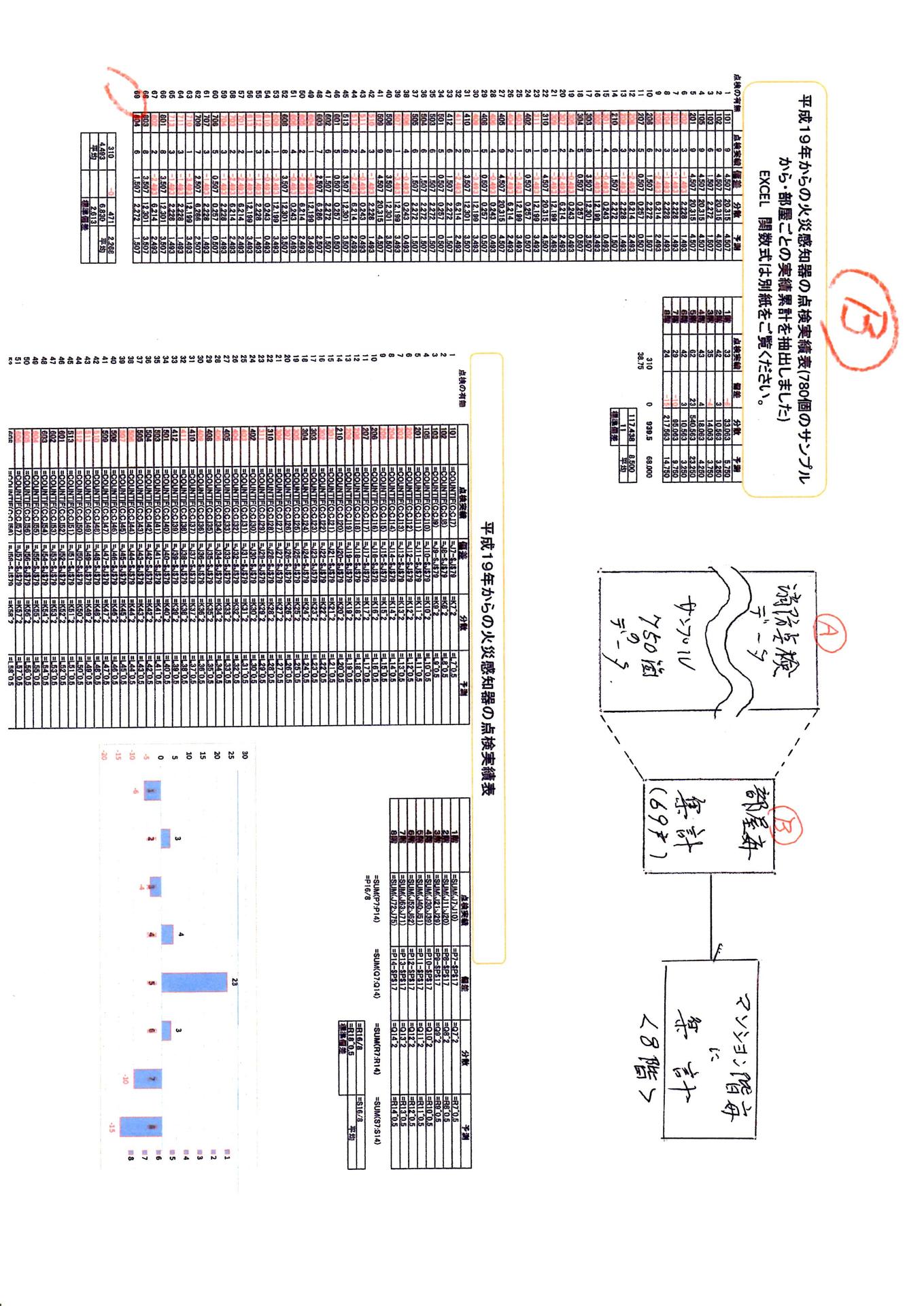
では「A表」から　ご説明しましょう、先週某ビルのマンションの部屋で　非常ベルが鳴りました　道路を通行する通勤者が火災と錯覚して黒山になりました。原因は定かではないが「火災時に知らせる感知器」が誤作動した訳です。私猿は知人のマンションを訪ね　建物管理業界を知りたくて、別紙A表を入手しました。次に示す資料は、近隣の同業他社様が日ごろ火災報知器を点検していた作業簿です。ご覧ください　約７８０箇所の貴重な火災感知器の点検記録です。しかし　これだけ見ただけでは内容は容易には把握できません。

よって　別紙B表のように・・・EXCEL関数の　＝COUNTIF（範囲、探す対象項目ここでは部屋番号）・・・を代入すると、例えば「102」を指定すると　102　が　9　個ある 。 求めてくれます。B表の中の左がその結果見本です。

一部グラフにしました、次の表はマンションの階層ごとに点検した回数です次のグラフは部屋ごとの点検回数です。読者にありては自分の身近なデータを使って猿まねして見てはいかがでしょうか。

関数式（COUNTIF）を使って、条件に一致するデータの個数を求める （事例研究）

条件に一致するデータの個数を求める 。 関数 式    COUNTIF（範囲、検索条件）に代入することで、　多くある　データの中から　条件に一致する個数を求めてみました。

今日は　日ごろ　管理している「温水ボイラー」の取り換え実績を見せて頂きました。よくできていましたご覧ください。ボイラー記録で過去1990年以降今日まで25年間の交換実績が残されているのには感心しました「追跡記録が欠如していても：過去のサンプルで21世紀の予測」が現代の統計学では可能なのです。マンション管理の同業他社さまの中でここまで実績を次の世代まで残せるでしょうか。すごい！！

 

実績表です。また　これは予測値が追加しています。数値管理をするには　ぜひ効率よく応用できる事例を　ご覧ください。コピーできます。

 

 

母集団からサンプル摘出分析 新たな発見を楽しんでいます

子供（サンプリング）を見れば　親（母が推測できる）がわかる。これの例えは人の社会のこと。

統計分析を行おうと思えば　全数調査が出来たらよいが・・・・・・　現実は困難である。そこで　サンプル情報から母集団を推測　手法とします。

①工場の流れ作業の製品出来上がり検査から新たな商品誕生の品質の予測。

②未知の世界感を　現在ある情報から　推測する。

③過去の情報から　未来を予測する。

④最後に　分析推測値が　現実に利用できるかを　信頼確率で　検証します。例えば　90％　95％　99％　等が信頼できるといった具合です。99％宝くじが当たればよいですね（笑い）。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

推測統計の扉を開く前に「分析ツールでデータ分析」を実行してみよう。

①EXCEL　の　データを開こう。

②データ分析を開いて(サンプリング）今回は　（A)10個のデータの中から　（B)５個のサンプルを選択されます。つまり１０個の中から５個の乱数を発生させ　任意に　人の意志によらず出力します。

　

　以下は、昨年の　天満橋の通行調査実績を参考に　ダミー扱いで（９０個中の中から　９個のサンプル）を選びました。ご覧ください。

③サンプリングを　を開こう。入力範囲（ここでは調査NOを打ち込もう）　ランダムの標本数を　入力しよう。

④さらに、　分析ツールから　基本統計表を使いましょう。赤い表で出てきたのが基本統計表です。。

⑤比較してみましょう。。

 答えが出来ました　実際の９０か所のデータは　左の表です。　右は私が推測しました、サンプル数は９か所ですが、全調査と比較して見ると　95％以内の推測が出来ました。今回の挑戦は　真の母集団対して　95％の確率以内のダミー推測母集団を求めることができました。と言うわけです。

統計の猿　でした。　　　　　　　　END　　

一年間 統計の猿 の原稿を 見てくださいましてありがとうございました。

　私（統計の猿）の原稿ご覧くださいましてありがとうございました。今後もよろしくお願いします。

　振り返れば　他の読者の皆さんに意図するところを　お伝えすることの難しさが身をもって感じています。統計学の奥深さを発見しましたが昨年発表しました内容は　ほんの一部です、つまり　統計学で言うと　「記述統計」といって　データを整理してその特徴を捉えることの勉強でした。

２年目は　推測統計の勉強をしたくなりました、それは何ですか？　それは　部分をみて、全体の様子を知る方法です。昨年の天満橋通行量調査は全調査でしたが、推測統計は・一部の標本調査から分析することで母集団（実態）を浮き彫りにすることなのです。（推測には・点推定と区間推定つまり幅を見て推定する方法があります参考まで）

例①選挙前の事前調査（出口調査データ当選者の予想）

②味噌汁の味見から　家族への食卓への料理の提供。

③喫茶店の売り上げ実績からのデータから、今後（未来）の営業展開予想を推測する。

④マンション管理での法的点検項目に関する、経年による劣化の推移を数値化して、積立金予測等に活用する。（横浜マンション傾き早期発見）

　おかげさまで　読者の参加者数は　　10,099名の閲覧者がいらしゃいました。詳細は次のようでした　　統計に関心が多い読者さまが　学習して　社会の実態を分析することは　不特定多数のお人に貢献できると信じています。　私の閲覧者数は・この部分をクリックしてください。http://blog.goo.ne.jp/admin/access_count/

偏差値 Z とは

まず　添付資料を　ご覧ください。・・・・・・・・・・・・

 Ａ：通常「偏差値」とは　観測値Ｘ　から　平均値　を引く（　－　）と　差が出ますこれを偏差と言います。

Ｂ：また、偏差値Ｚ（ゼット）とは　　Ｚ＝　は　これを　A項での（偏差値）を　標準偏差値で割った　結果を言います。

　Ｃ：例外的に　、　日本では　学校の成績の数値化に採用しています、　学業成績では　偏差値Ｚ＝５０点プラス（+）　　　　（10×（（Ｘ-平均Ｘ）/標準偏差）　の公式から求めたものです。平均点の　５０点　とした場合の　得点である、標準偏差は　10　である。　詳しくは　下記　添付資料をご覧ください。

この　レポートを　Ｅｘｃｅｌ　で　猿まね　実施して　検証ください。　

変量標準Ｚ とは

母集団　が　複数の場合　の　比較　手段とした　同じ　マスで　量ろう・・事例研究。。

 

複数の母集団から得た データ間 を 比較する方法は ・・・

複数の母集団から得た　データ間　を　比較する方法は　・・・　同じ　マス升　で比較できないでしょうか　別紙公式を活用して試算してみたいですね。印刷できます。

例：センター試験の「国語」に特化して　取り組んでみました。

　センター試験の　国語の　受験者は　５０７,７９１名　の中に　統計猿君が　受験者の中に含まれて　いると仮定しましょう。センター試験の国語の　平均点は　64.69点であった。　　受験者の統計猿は　自己採点が　ダミー　７０点　と仮定する。

下記の　公式に　代入すると・・・・標準化Ｚ＝（70-64.69）/18　となります　答えは　0.29　％　である。つまり　507,791人の受験中　146,388　人位　とななり　１００人中２９番目　でありました

　　　　　　　　　　　　　・・・・偏差化Ｚ＝50+（10×｛（70-64.69）/18｝　となります　答えは　52.59点　である。つ　　　まり　センター試験の平均値　64.69点　より　52.59-64.69＝　マイナス-12.1点　であった。

標準化を 求める 方法を 復習してみました。

標準偏差値を利用して（代入して）標準化の出し方を復習してみました。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

　お子さんを　お持ちの　お母さんから　別紙のような質問がありました。つまり　簡単に言うと「Ａ君とＢ君は中学時代は同じ学校であったが　高校は　訳あり　別々の　高校に通うようになり　試験のたびに　点数を見せ合うことで競っていたようだ　それをできなくなりました。　この春の「大学入試センター試験」を受験したようだ。

　しかし　Ａ高校の平均点６１点の「猿Ａ君」と　Ｂ高校の平均点６１点の「猿Ｂ君」との両校の学校の　標準偏差値　はほぼ同じで　４.４点  であるという。両君は　大学進路選択に迷っていました。

　さて　どのように　説明をしたら　良いでしょうか・・・・・という悩みです。

 

 

　高校が違うと　難易度が違い比較することが　例えＡＢ君が６１点として　同じ実力と錯覚し進路判断には　困難ではと　思われます　なぜなら「偏差値や学生さんのテストの平均点が同じでも」Ａ高校の全生徒の平均点が違うと　「標準偏差を求めるにあたり　平均値からの離れ　つまり　偏差が違うことを学びました」ことを　思い出しました。

　よって　このような　母集団（学校）が　違うときは　共通な「升　マス」の中に入れる必要があるのでしょうかね！！。よって余り自信がありませんが　両高校の「高校の偏差を」1イチ　を　100％になるように正規分布に　いわゆる標準偏差化（化）に加工することで数値化できる方法が考えられます。

　＜一度試してみます＞

①正規分布図において　平均値を　ゼロ：0　とし　さらに　標準偏差値は　イチ：１とする必要がいります。

②別紙　のＡ君の　偏差化（0.22）となり　Ｂ君の　偏差化（-0.92）となります、この意味は　平均値からの離れを数値化して表現しています（正規分布図）よって　見えるのは　比較して　ＡＢ君の間に　-0.92＜Ｚ＝0.16（比較者間）＜0.22　に多少の開きがみえます。あとは　ご本人の意思決定ではないでしょうか？　　余談ですが　株式において２社比較するにあたり　株価は同じでも　出来高が　違うまたは　利益率等が見えないに類似して？？

③その公式は　Ｚ＝（Ｘ - 平均Ｘ）　÷　標準偏差値　・・・である。最後尾に貼り付けあります。

④参考に：標準偏差値　の　代入応用は　これからも　良く使われています。最後尾に「センター試験の結果」がホームページで告知されましたので　一度　開いて見てはいかがでしょうか。

 

一度教科ごとの　実力を　比較　試算してみては　如何でしょうか。

 　余り　自信が　ありません　読者の方で　「検証」してから　お使いください。　統計家を志す猿より。

読者さまへ 誤解を招かないよう 母集団 と 標本観察サンプル を明確に区別しました。

　最近　ビッグデータ　という言葉を　よく聞きますね、統計数値が新聞等で報道が多くなりました。報道の中に必ず調査した方法が前提で発表されています。例えば「選挙：出口調査で　○○は当選確実」という前置きがされています。聞き手は「出口調査？最後まで油断できないね」と思うでしょう。　

　統計学でこれに似た考えがあることに気が付きました。例えば私の道路の通行調査で見ると「三ノ宮方面行きの　標準偏差が２7台」とレポートを作成させて頂きましたが、調査がどのような方法で実施したのか　明確に　母(母集団)　と　子（標本）　区別説明が大切と思っているのです。

　よって　今回の調査の数値には　変更はなく　事実ではありますが　先週の統計数値は　１２時間の調査サンプルではなく、６時間の調査をした結果を告知しています。

つまり「母集団」は１２時間であるが　実際調査した時間は１時間実施して１時間休憩を行い実質６時間調査をしているのです。　これを６時間の「標本」といいます。調査した数値は標本から得たデータです。

　統計学では　母集団の　一部を調査分析することで　全体を推測することとなっています。これを推測統計と言われています。

添付資料の文中において　「発生率と生起率」という文語がありますが　発生率は過去のものに使う　が　生起率は未来に使う　確率をいうそうです。（情報学）

　時々「統計はインチキであてにならない」と声を聴きますが　これも調査者が丁寧な調査方法を明確にしていないことが原因ではと気が付きました。別紙を　再度ご覧くださいますようお願いします。

 

Ｅｘｃｅｌ ・統計関数STDEV ・ を使って「標準偏差」を求めてみました。

４月８日の日記に掲載しました　筆記による　基礎計算（標準偏差）との　比較をしてみました。

①　統計関数である　Ｅｘｓｅｌ関数での方法を　復習してみました　別紙をご覧ください。

②　筆記計算と、Ｅｘｃｅｌ統計関数＝ＳＴＤＥＶ（ｘ1～ｘn）方法　との　結果比較表をご覧ください。

③　感想1：標準偏差の筆算では　計算根拠が　良くわかりました。これで　標準偏差の計算が出来るようになりました。

④　感想2：今後統計関数ＳＴＤＥＶ（　　、　　）区間方法で簡単に求めれるようになりました。

④　今後は　標準偏差値が　大きいほど　平均値から　分散（離れている）。また　標準偏差値が小さい程平均値に集中していることを　　復習したく思っています。調査目的が　道路の混雑度であるなら　標準偏差値は大であれば　良くすいていると解釈できます。

つまり正規分布図で説明がつくのです：例（標準偏差=２７台）の時は　平均値112.4-27＝85.4台です、　　又は平均値112.4+27＝139.4台　となります。つまり正規分布図の85.4～139.4の間に　現場調査をしました交通量調査の３分の2のサンプルがあることに解釈できるのです。視点を変えて学校の成績がこの範囲にあれば　クラスのなかで平均点前後にある（位置）とみることが出来ます。下記の表は統計Ｅｘｃｅｌ関数で行った表です　ご覧ください。

　　

標準偏差の 作成 方法

標準偏差の　作成　方法には２通りの方法があります　①統計関数（ＳＴＤＥＶ）を使って行う方法と　②実際にＥxceLによる方法があります。　◎読者のお方に　ExceＬ関数や  将来プログラム操作の中での　「答えが一瞬に出るが」なぜ　この答えが出るものの意味が説明または解明できないことに　遭遇するであろう。◎たとえば　円の面積の「3.14」という円周率の検証の勉強を待たずしてお使いの時に　疑問を感じるに似たような「ブラックボックス」に入るのを防ぎたいものです。

　さて過去に　私事　猿の　経験で「標準偏差」の勉強をもう一度　復習を　してみました。

　多くの　サンプルから　分析して「標準偏差」の　導きには　4回の手間をかけることで「標準偏差」のもつ意味がわかるからです。

①　まず　今回は　道路の通行量の情報を　把握することしますが　皆さんはセンター試験の内容でもかまいません

②　データを集計して　平均値を基本として　観測値との差を出します。この差には「+と-」があり　これを統計学では「偏差値」といいます。

③　②項で求めた　偏差値を二乗します　出た数値は　分散値　といい「値はすべて+」です。

④　③項で求めた　分散数値はの　総計から平均値を　また二乗根であるので　（√　）　ルートにより　元の　台数に　変換します。

 

⑤　その他　　関数　を　添付しておきました　参考になさってください。印刷できます　よく見ると　簡単なことと　お気付きになられるでしょう。

⑥　統計を学び　ある事象を分析することで　知恵となり　生活や企業の中で新たな発見が見えて来ることを期待します。

⑦　当ブログに多くの閲覧　ありがとうございます　４月の８日の閲覧実績は７7名さまでした。　今回の私の調査は道路調査でしたが、夕方から地方のトラックが神戸港方面に集中している事象が見えてきました。　・・・・・・・・・

読者の身近な周辺にある　◎お子様の学業成績の分析　　　◎個人商店には売り上げ分析      ◎マンション管理統計　　　◎ビル管理の　電気消費量の管理　　　◎訪問看護の聞き取りアンケートの記録分析等・・・いくらでも　身近にあります。

　この機会を利用して　ぜひ身に着けて　社会のために　お役立てくださいますよう　ご案内いたします。

統計家を志す　統計の猿　より　　　　　　　　　　　　　　　平成２８年４月９日（土曜日）

 

標準偏差値の求め方

　交通量の　情報をもとに　「標準偏差値」の　求め方を　投稿しました。

統計の勉強を始めたときは　「標準偏差」とは　なんの意味だろうと　思っていました。今高等学校の　数学Ⅰ　で習うようになりました（指導要領）。

つまり　別紙レポートを　ご覧ください・・筆記しましたので　計算方法(本表の分散末尾の・１０９９と６０９は　例えば1099＾0.5　としてくだされば標準偏差は33・25 となります。

標準偏差値の単位は　この場合は「通過台数：台」です。

読者の　皆さんの　身近に　①お買い物の　伝票　　②体重記録　③お子さんの　成績(偏差値と標準偏差値とは意味が違います・ご注意)　・・等など　　私のレポートを参考に「猿まね」してみてください意外と楽しいです。

さらに　意味は「計算結果　値」　は　平均値からの　離れを　意味します。　

 

統計学問がこれほど普及していること知らなかった

統計学問がこれほど普及していること知らなかったのは「統計家を志す猿」である７０代の私だけだった（苦笑）

既に　社会通信教育において　動機は過去の体験から統計の必要性に気が付いて勉強を始めました。しかし２年間統計学習を体験して人並みに近くなり　ご満悦していましたが　すでに　平成２５年頃から小学生から高校生の教科書に盛り込んでいることに気が付いたのです。

私は、独学の２年間でしたが　学習の入り口が見つからず　ずいぶん　遠周りしていることに気が付いたのです。

よって　これから　統計の　勉強してみようと　思っていらしゃる読者に　参考になる図書を発見しましたので　お知らせしましょう（図書の販売目的ではありません）

私の身近にいらしゃる「飲食店」の店員さんが　興味半分「重回帰曲線」に取り組み　皆目分析できない羽目になりました。基礎の勉強が大切ですね。

そこで　別紙（技術評論社平成１５年初版：統計学の図鑑）が　全体の流れが把握できるのではないでしょうか。次は私たちの近くには「ビックデター」がたくさんあります活用して楽しい生活に役立つはずです。最後に義務教育での取り組み内容を貼り付けました　詳しくは書店での図鑑をご覧ください。

統計学を学んで２年間を振り返って

統計学を学んで２年間を振り返って

読者の皆さんには　ブログを通じて昨年6月以降　現在３月までご支援ありがとうございました。

私のブログは、学習日記風に投稿させて頂きました。学んだことを第三者さまに　ご報告することは　大変難しいことと実感しています。

実は　教本に背をおされ「身近の情報を使って体験することが学びの内容が身につく」と教わりました。

よって　これまでの　私の　勉強の取り込みをご報告します、何かのお役に立てばと思います　ご覧ください。まず教本をご覧ください。

◎最初の教本です　内容は著作権上割愛させていただきます　「現代統計実務講座」です。

◎学校に例えれば　中学時代の基本である内容です「多変量解析実務講座」です。

◎高等学校程度の内容ですが　応用例が主体でした「エクセルによるデータ解析コース」です。

最後に　今日までの　統計学問に取り組んだ　内容をご覧ください「統計の学び2カ年を振り返ってみました」です。

　

内閣府にある「統計委員会」の動き 新聞に掲載ありました。

◎　統計内容の精度上げる取り組みが「日本経済新聞」に掲載されました。ここでいうビックデータとは現在のＩＴ社会では過去の類を見ない情報量が蓄積されていますがそこで新しい統計的手法を模索されています、その対象を「ビックデータ」と言えるでしょう。

◎　また　大阪市中央区の　国勢調査結果の論評が公開されました。　→　　　　ご覧ください。