私のブログの閲覧者70名でした(2016・12・16)小難しい原稿をお読みくださるお人がこんなに多くいてくださるには読者の統計に関するレベルの高さには関心しています。
振り返ればブログ公開実績15か月になります その間閲覧者は19,608名です1日平均43名ということです、1日最高では150名 最低では38名の事もありました。原稿内容の反省しながら 優しく時にはレベル上げることもさせて頂きました。
楽しく感じることは かなり専門的な内容でも30名閲覧くださっている読者さまには尊敬いたすところです。
では前置きが長くなりましたが では今日の日記は インターネット通信で 商品の販売データもとに 予測値の分析を透明方式で実施しています。 猿まね・して楽しんで見てください。
・・・・・・・・・・・・・・記・・・・・・・・・・・・・・・・・
解を 求めて 実体験してみました。
今回は この記述を私のノートに、見立てて実際の 取り組みの手順を透明にすることで実力が付くと信じています。
時には迷路に入り読者さまにご迷惑をおかけするかもしれませんがよろしくお願いします。
正解のない難問に挑戦してみます。・・・・・・・・・
・・・・・・・・・・・・・・・・
別紙①をご覧ください。

・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・統計の猿より・・・・・・・・・・・・
振り返ればブログ公開実績15か月になります その間閲覧者は19,608名です1日平均43名ということです、1日最高では150名 最低では38名の事もありました。原稿内容の反省しながら 優しく時にはレベル上げることもさせて頂きました。
楽しく感じることは かなり専門的な内容でも30名閲覧くださっている読者さまには尊敬いたすところです。
では前置きが長くなりましたが では今日の日記は インターネット通信で 商品の販売データもとに 予測値の分析を透明方式で実施しています。 猿まね・して楽しんで見てください。
・・・・・・・・・・・・・・記・・・・・・・・・・・・・・・・・
解を 求めて 実体験してみました。
今回は この記述を私のノートに、見立てて実際の 取り組みの手順を透明にすることで実力が付くと信じています。
時には迷路に入り読者さまにご迷惑をおかけするかもしれませんがよろしくお願いします。
正解のない難問に挑戦してみます。・・・・・・・・・
・・・・・・・・・・・・・・・・
別紙①をご覧ください。

・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・統計の猿より・・・・・・・・・・・・
売り上げ表 分析を 3方法 比較してみました。
① LINEST関数により 回帰式を発掘しました:Y=*******
② 散布図グラフによる 回帰式を発見しました:Y=*******
③ EXCEL2010 PCにより回帰統計分析を実施しました:Y=******
①②③いずれも Y=196.192 + (-0.1029x) ・・・・Xに代入してみてください。明日の売り上げが推測されます。またP値が0.3ですから0.5より少ないので この推測値は十分信用できるというわけです。Pはパンチと記憶して下さればパンチは小さいほうが良い。
(追記昨年秋から1年間投稿しています基礎勉強には参考になるでしょう)
私は 社会通信教育(文部科学省認定):財団法人 実務教育研究所の生徒として「統計士」認定書を頂きました。このブログの環境をお借りして「復習させて」頂いています。
JA全農の職員様に特におすすめいたします、頑張ってください。私は現在山林の木材の成長とその山の10年後の木材体積計算を学習中です。投稿原稿が完成しましたら投稿予定です。
では3方法の分析表をご覧ください。


統計の猿 投稿 2016年12月8日深夜発信
① LINEST関数により 回帰式を発掘しました:Y=*******
② 散布図グラフによる 回帰式を発見しました:Y=*******
③ EXCEL2010 PCにより回帰統計分析を実施しました:Y=******
①②③いずれも Y=196.192 + (-0.1029x) ・・・・Xに代入してみてください。明日の売り上げが推測されます。またP値が0.3ですから0.5より少ないので この推測値は十分信用できるというわけです。Pはパンチと記憶して下さればパンチは小さいほうが良い。
(追記昨年秋から1年間投稿しています基礎勉強には参考になるでしょう)
私は 社会通信教育(文部科学省認定):財団法人 実務教育研究所の生徒として「統計士」認定書を頂きました。このブログの環境をお借りして「復習させて」頂いています。
JA全農の職員様に特におすすめいたします、頑張ってください。私は現在山林の木材の成長とその山の10年後の木材体積計算を学習中です。投稿原稿が完成しましたら投稿予定です。
では3方法の分析表をご覧ください。


統計の猿 投稿 2016年12月8日深夜発信
身近な生活 改善から 応用実践してみよう。
統計を学んでいらしゃる読者の中にマンション管理員様が今年の12月総会を期に65歳となり退職されることの情報が入りました。
私は「Mさん」を訪ねてみると下記のような提案書を拝見させていただきました。
このマンションは屋上に水槽をなくて1階から加圧式で各部屋に送りこんでいるそうだ、電気が停電となればマンションの水洗トイレは機能しないことを承知していらしゃるという。
管理会社は まったく聞く耳を持たず放置しているようだ。
そこで自ら 地震災害時に備えて別紙を作っていらしゃる・・・
統計学を難しく考えることなく実行してくださっているのには 関心しました。
統計家を目指す猿の見方は、全体の水道量から逆算して電気供給が1時間停電した時の生活に必要水量を試算手順からみて、統計学で見れば「母集団から標本」を推察に見えるのです。
・・・・・災害時にマンションの生活維持するには「いくらの水量」が必要か試算している様子をご覧ください。


統計を学んでいらしゃる読者の中にマンション管理員様が今年の12月総会を期に65歳となり退職されることの情報が入りました。
私は「Mさん」を訪ねてみると下記のような提案書を拝見させていただきました。
このマンションは屋上に水槽をなくて1階から加圧式で各部屋に送りこんでいるそうだ、電気が停電となればマンションの水洗トイレは機能しないことを承知していらしゃるという。
管理会社は まったく聞く耳を持たず放置しているようだ。
そこで自ら 地震災害時に備えて別紙を作っていらしゃる・・・
統計学を難しく考えることなく実行してくださっているのには 関心しました。
統計家を目指す猿の見方は、全体の水道量から逆算して電気供給が1時間停電した時の生活に必要水量を試算手順からみて、統計学で見れば「母集団から標本」を推察に見えるのです。
・・・・・災害時にマンションの生活維持するには「いくらの水量」が必要か試算している様子をご覧ください。


総務省のホームページです 御覧ください。統計学を学ぶものにとって 大切な情報があります。
下記のホームページhttpをコピーして 検索して 御覧ください。「統計の環境」が出力されます。ぜひ知っておいてくださる方がよいと思います。
http://www.soumu.go.jp/toukei_toukatsu/index/seido/stkankyo.htm
推測統計学びの準備(確率)について復習しています。ここでいう確率とは サンプルの抽出方法に「無作為抽出」方法があることを知りました。
このレポートを より理解するには 野球球団を母集団に例えて 「某野球球団の・ストライクゾーン 0123456789 記録」と読み替え イメージしてみては 如何でしょうか。さらに無作為試行(A選手・B選手・C選手・・・・・・)の実績を把握することで 球団の全体を評価していいのでしょうか・・・という学びの復習です。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
その無作為方法で 抽出した 分析の 結果のデータは どの程度信頼してよいか疑問がわきますね、
つまり分析結果レポートの中に 「 P値 」欄があります これは何を意味するのか興味がわきました。
まずは私(猿)の 過去の提出した学びのレポートをご覧ください。

①回帰統計・・・P値欄を確認ください・・・・
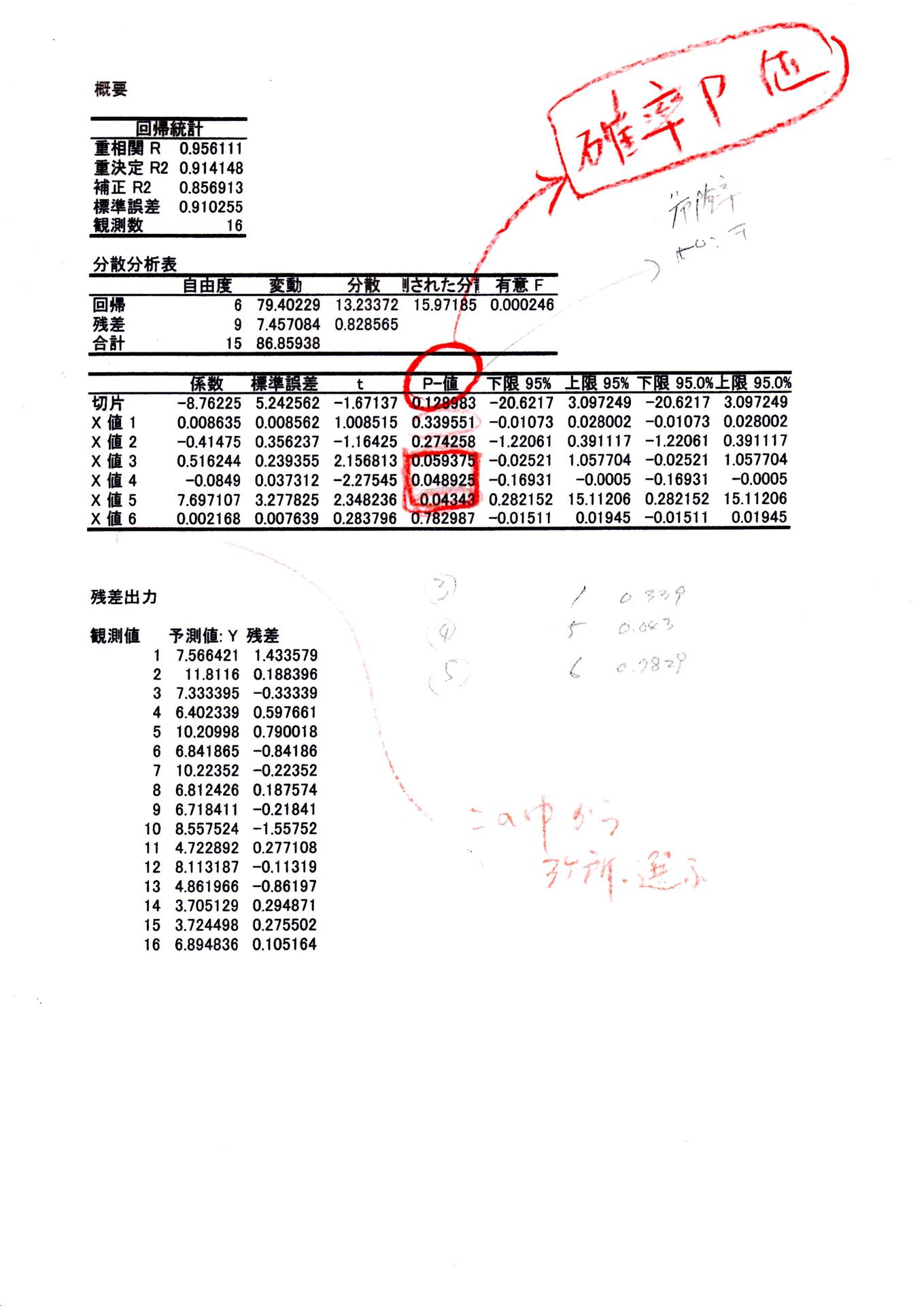
・・・・・・・・・・・・・・・・・・・・・・・・・・・
②無作為抽出する上で 考慮したい 母集団の本質を真実に把握する必要があります。しかし統計学では 100%言い当てる事は求めていないようで、そこで「P値」で信頼度を数値化していることが解りました。
①の資料で P値は パンチ とも言い パンチは 0.05以上は危険であり 信頼できないと解釈しています、パンチを受けるなら、P=0.048 P=0.043のように 小さいほうが良い と記憶していれば役に立つでしょう.
③では実際に検証してみました。 別紙の表1は 乱数を発生させて 「0 から 9」までを無作為に発生しています。 この表の中に 0は6個 1は14個 ・・・・9は5個 の表を作成しました。表中9最小値=5%であり 表中1最大=14%となりました、この出現率の誤差は(14-5=9%)であることが解りました。
統計学では 無作為に標本を抽出すれば 解は 10%以内であることを定義つけしてあります。これの説明を言い換えると誤差は10%以内に収まることを知りました。母集団を診察するにあたり標本誤差が少ないほうが良いことになります。
別紙1の標本ダミーをご覧ください
拡大レポートです。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
別紙2をご覧ください。別紙1に類似しています。

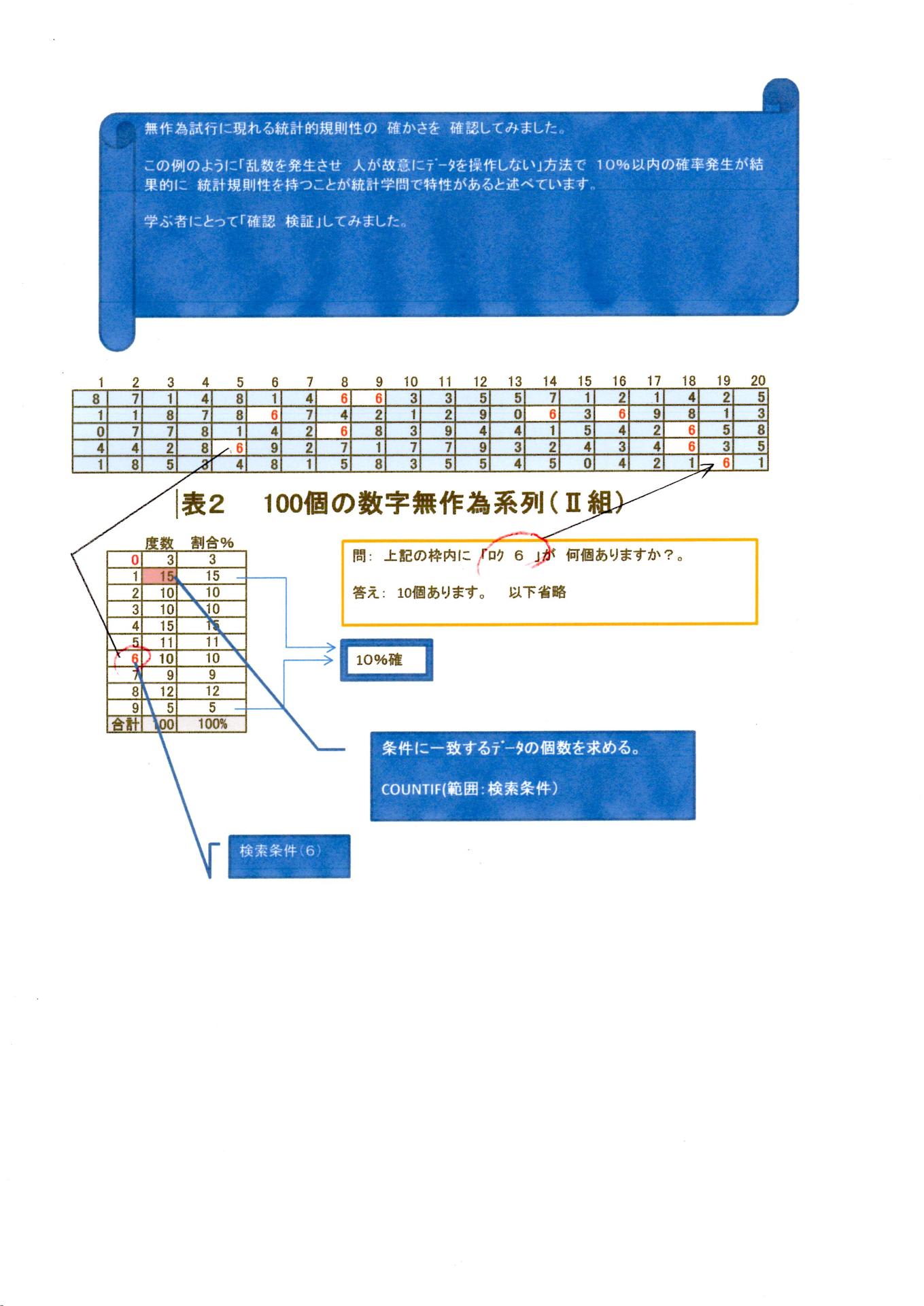
・・・・・・・・・・・・・・・・・・・・・・・・・・
さらに別紙3をご覧ください これは 無作為Ⅰ プラス 無作為Ⅱ の表を合成した例題です。いずれも別紙1・別紙Ⅱ・別紙Ⅲ いずれの例題も 最小最大割合の誤差は 10%以内にあります。
母集団から抜き取られる サンプルの割合 誤差は 少ないほうが良いわけである。
別紙3をご覧ください。

拡大レポートをご覧ください。
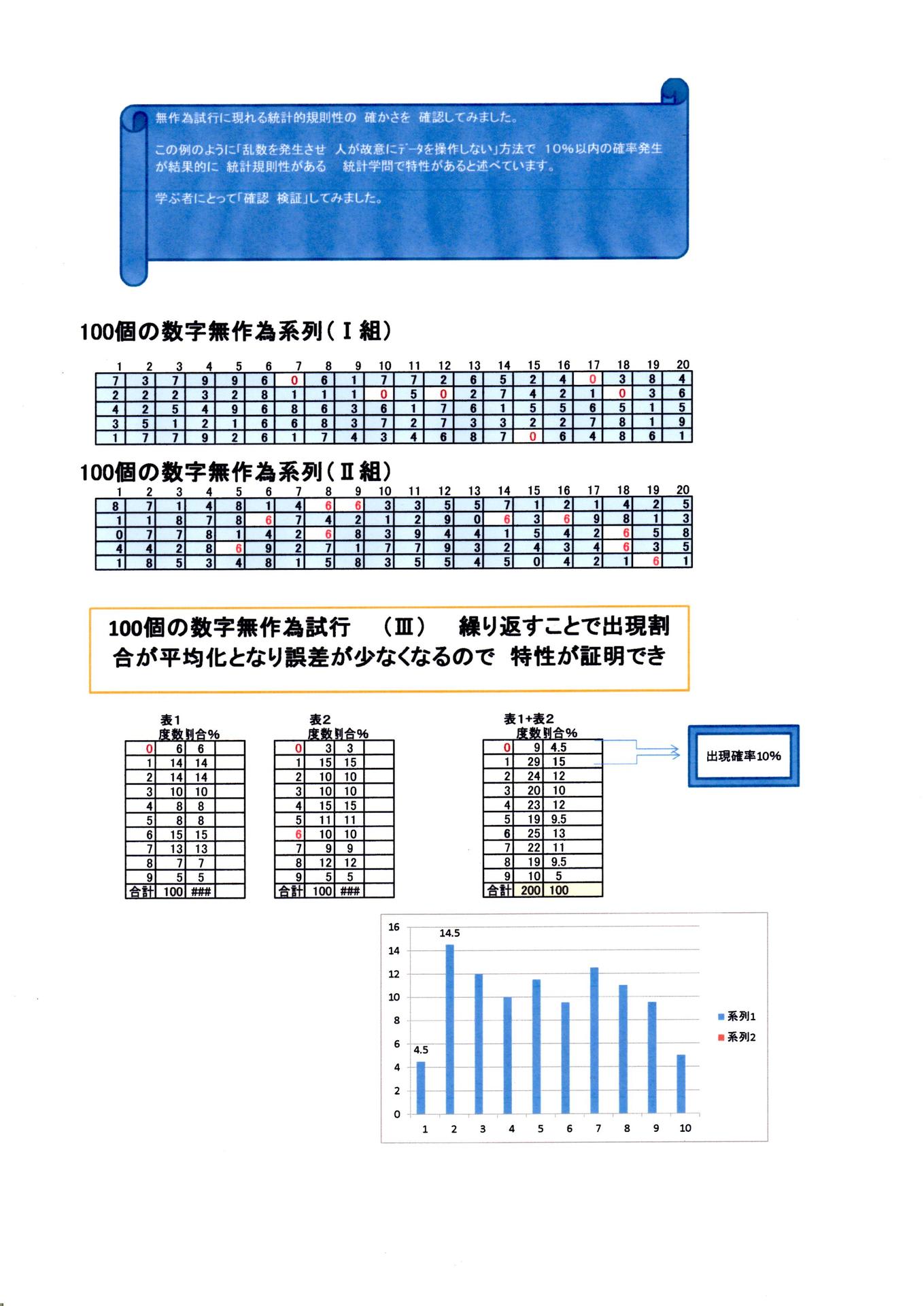
・・・・・・・・・・・・・・・・・・・・・・・・・・・・
無作為に 抽選に参加するとすれば サイコロ方式 又は トランプ方式 で占う どちらにしますか、以上確率はどちらが良いでしょうか。
標本抽出にあっては「無作為」に関して 概要を深めたい又学びたい読者様には 書店に販売しています 図書p70を参照ください 漫画ふうになっていて 良く解る本です。

以上 記述は 統計の猿でした。
・・・
このレポートを より理解するには 野球球団を母集団に例えて 「某野球球団の・ストライクゾーン 0123456789 記録」と読み替え イメージしてみては 如何でしょうか。さらに無作為試行(A選手・B選手・C選手・・・・・・)の実績を把握することで 球団の全体を評価していいのでしょうか・・・という学びの復習です。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
その無作為方法で 抽出した 分析の 結果のデータは どの程度信頼してよいか疑問がわきますね、
つまり分析結果レポートの中に 「 P値 」欄があります これは何を意味するのか興味がわきました。
まずは私(猿)の 過去の提出した学びのレポートをご覧ください。

①回帰統計・・・P値欄を確認ください・・・・


・・・・・・・・・・・・・・・・・・・・・・・・・・・
②無作為抽出する上で 考慮したい 母集団の本質を真実に把握する必要があります。しかし統計学では 100%言い当てる事は求めていないようで、そこで「P値」で信頼度を数値化していることが解りました。
①の資料で P値は パンチ とも言い パンチは 0.05以上は危険であり 信頼できないと解釈しています、パンチを受けるなら、P=0.048 P=0.043のように 小さいほうが良い と記憶していれば役に立つでしょう.
③では実際に検証してみました。 別紙の表1は 乱数を発生させて 「0 から 9」までを無作為に発生しています。 この表の中に 0は6個 1は14個 ・・・・9は5個 の表を作成しました。表中9最小値=5%であり 表中1最大=14%となりました、この出現率の誤差は(14-5=9%)であることが解りました。
統計学では 無作為に標本を抽出すれば 解は 10%以内であることを定義つけしてあります。これの説明を言い換えると誤差は10%以内に収まることを知りました。母集団を診察するにあたり標本誤差が少ないほうが良いことになります。
別紙1の標本ダミーをご覧ください

拡大レポートです。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
別紙2をご覧ください。別紙1に類似しています。


・・・・・・・・・・・・・・・・・・・・・・・・・・
さらに別紙3をご覧ください これは 無作為Ⅰ プラス 無作為Ⅱ の表を合成した例題です。いずれも別紙1・別紙Ⅱ・別紙Ⅲ いずれの例題も 最小最大割合の誤差は 10%以内にあります。
母集団から抜き取られる サンプルの割合 誤差は 少ないほうが良いわけである。
別紙3をご覧ください。

拡大レポートをご覧ください。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・
無作為に 抽選に参加するとすれば サイコロ方式 又は トランプ方式 で占う どちらにしますか、以上確率はどちらが良いでしょうか。
標本抽出にあっては「無作為」に関して 概要を深めたい又学びたい読者様には 書店に販売しています 図書p70を参照ください 漫画ふうになっていて 良く解る本です。

以上 記述は 統計の猿でした。
・・・
大阪城に 猿が 統計の猿が 出没(笑う)
平成28年10月27日(木曜日) 晴れ 気温18.3度 6時30分からのNHKラジオ体操に 統計の猿も 参加させていただきました。
大阪城は「真田丸」一色 幟旗(のぼり)は朝日を受けて元気 はつらつ!! それに負けずに頑張っていらしゃる大阪城付近の「侍さむらい」いや 40代から80代の男女も 合図にあわせて「ぴょんぴょん」🎼🎼と元気に体操!!
参加者の前では 日の出の朝日を浴びて天高く 黄金の輝く大阪城でした。こんな贅沢な環境の中で幸せ者と 猿は感じました 元気をいただき有難うございました。
参加者人員は なんと 南門 295人(11月6日・日曜日・追加調査240名) 北門 (11月5日追加調査130名) でした。



・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
平成28年10月27日(木曜日) 晴れ 気温18.3度 6時30分からのNHKラジオ体操に 統計の猿も 参加させていただきました。
大阪城は「真田丸」一色 幟旗(のぼり)は朝日を受けて元気 はつらつ!! それに負けずに頑張っていらしゃる大阪城付近の「侍さむらい」いや 40代から80代の男女も 合図にあわせて「ぴょんぴょん」🎼🎼と元気に体操!!
参加者の前では 日の出の朝日を浴びて天高く 黄金の輝く大阪城でした。こんな贅沢な環境の中で幸せ者と 猿は感じました 元気をいただき有難うございました。
参加者人員は なんと 南門 295人(11月6日・日曜日・追加調査240名) 北門 (11月5日追加調査130名) でした。



・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
現場の調査データが有れば 簡易な 統計分析ツールが 搭載されています。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
一度 確認してみてください。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
まずEXCELを開いてみてください, 例えば 最初は 乱数表で 猿まね して見てください サンプルデータなしで取り組んでみましょう。ここで計算は省略してね!!(参考:右クリックするとコピーが取れます 自分のメモ書庫に転記OK)


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
拡大すると ・・・・ご覧のように19項目あります。
ご覧ください。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
最初は ①乱数発生 が良いでしょう。なぜなら読者さまが サンプル データをお持ちでない場合は「サンプル ダミー」として練習に使えます。
例えば

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
②つぎは 基本統計量 が良いでしょう。 調査データの特性が見えてきます。
例えば

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
③つぎは 相関関数 が良いでしょう。 データ間の関係があるのか ないのか 良くわかります。選挙や株価と出来高を相関してみてください
例えば

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
④つぎは ヒストグラム が良いでしょう。 これは 100%を 全数を Ⅰイチ と見立てたグラフがで来ます つまり度数値グラフです。
⑤つぎは 順位と百分位数 が良いでしょう。
⑥つぎは グラフ表現に適している 移動平均法。
以上は 乱数を 使って 体験してみました。これは私(猿)の方法です。
後は 自分で調査したデータが あるほうが 良いようですね。
⑨回帰分析を 試してみてください。書店では いろいろ 良い見本があります 私は 日花弘子さんの 「EXCEL統計解析入門」をよく使っています、 私は投稿原稿を編成する時は「文部省認定:実務教育研究所」の教本に準じて実施していますが この本は参考になる本です。

⑦以上はある程度 記述統計 を 学習していた方がよいかも。
・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
以上は 統計家を目指して 勉強している 「統計の猿」が記述しました。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
一度 確認してみてください。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
まずEXCELを開いてみてください, 例えば 最初は 乱数表で 猿まね して見てください サンプルデータなしで取り組んでみましょう。ここで計算は省略してね!!(参考:右クリックするとコピーが取れます 自分のメモ書庫に転記OK)


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
拡大すると ・・・・ご覧のように19項目あります。
ご覧ください。


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
最初は ①乱数発生 が良いでしょう。なぜなら読者さまが サンプル データをお持ちでない場合は「サンプル ダミー」として練習に使えます。
例えば


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
②つぎは 基本統計量 が良いでしょう。 調査データの特性が見えてきます。
例えば


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
③つぎは 相関関数 が良いでしょう。 データ間の関係があるのか ないのか 良くわかります。選挙や株価と出来高を相関してみてください
例えば


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
④つぎは ヒストグラム が良いでしょう。 これは 100%を 全数を Ⅰイチ と見立てたグラフがで来ます つまり度数値グラフです。
⑤つぎは 順位と百分位数 が良いでしょう。
⑥つぎは グラフ表現に適している 移動平均法。
以上は 乱数を 使って 体験してみました。これは私(猿)の方法です。
後は 自分で調査したデータが あるほうが 良いようですね。
⑨回帰分析を 試してみてください。書店では いろいろ 良い見本があります 私は 日花弘子さんの 「EXCEL統計解析入門」をよく使っています、 私は投稿原稿を編成する時は「文部省認定:実務教育研究所」の教本に準じて実施していますが この本は参考になる本です。

⑦以上はある程度 記述統計 を 学習していた方がよいかも。
・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
以上は 統計家を目指して 勉強している 「統計の猿」が記述しました。




























