
「量子現象の数理:新井朝雄」第3章
(全体の章立ては記事のいちばん下を参照。全体の詳細な目次はこのページを参照。)
第3章:正準交換関係の表現と物理
- はじめに
- 予備的考察
- ヴァイル型表現
- シュレーディンガー表現のヴァイル型性
- ヴァイル型表現の構造 - フォン・ノイマンの一意性定理
- CCRの非同値表現とアハラノフ-ボーム効果
- 弱ヴァイル型表現
- 時間作用素
ノート
演習問題
関連図書
第3章の内容は冒頭で次のように要約されている。
量子力学の根本原理の一つである、代数構造としての正準交換関係(CCR: Canonical Commutation Relation)の表現論の初等的部分を、量子物理との関連を念頭に置きつつ論述する。また、CCRの変形から定義される時間作用素の概念についてもふれる。これは従来曖昧に論じられてきた”時間-エネルギーの不確定性関係”に対する一つの明晰な形を与える。さらに、時間作用素と状態の時間発展(生き残り確率)との関係について議論する。
ハイゼンベルクの不確定性関係を考慮すると、量子的粒子の粒子的描像における位置作用素Qと運動量作用素Pは次のような正準交換関係(CCR)に従うことは「量子力学の数学的構造 II:新井朝雄、江沢洋」で説明されている。
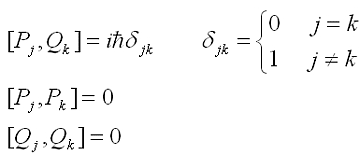
さらに外的自由度に関する限り、有限自由度の場合と無限自由度の場合も含めて量子力学は代数構造としてのCCRのヒルベルト空間表現として捉えられることも示された。有限自由度の量子力学と量子場の理論のような無限自由度の量子力学との違いは、有限自由度のCCRの表現と無限自由度のCCRの表現の違いとして把握される。
無数に存在するCCRの表現を解析することによって、量子現象があらわれる仕方を根本で支配する数学構造のひとつの相を根源から明晰に認識することが可能になるはずだ。そのためには無数にあるCCRの表現たちを本質的に異なるものとそうでないものとに分類、整理することが必要である。
シュレーディンガー表現のCCRとボルン-ハイゼンベルク-ヨルダン表現のCCR(参照ページ)が、表現形式が異なっていても、物理的にはまったく同じ内容を記述するものがあり、そのような表現どうしは物理的に同値であるという。他方、ある表現は別の表現と本質的に異なる物理的内容を内蔵している場合がある。このような二つの表現は物理的に非同値であるという。
この第3章では有限自由度のCCRの表現に限定して考察されている。つまり量子場の理論は含まれない。以下、表現の既約性、シュレーディンガー表現の既約性、表現の同値性、ヴァイル型表現、ヴァイル型表現の既約性、シュレーディンガー表現のヴァイル型性、ヴァイル型表現の構造が一意であること(フォン・ノイマンの一意性定理)、フォン・ノイマンの一意性定理からの帰結など数学としての説明とそれらの証明が25ページに渡って展開されている。
注意:ヴァイル(Weyl)の一般的な表記は「ワイル」だが、この記事では本書での表記に従って「ヴァイル」とした。
フォン・ノイマンの一意性定理からの帰結とは次のとおり。
Hを可分なヒルベルト空間、H上の自己共役作用素の組 {Qj,Pj}j=1~N はCCRのヴァイル型表現であるとする。このとき次の(i)~(iii)が成り立つような稠密な部分空間 D⊂H が存在する。
(i) 各Qj, PjはDを不変にする:D⊂∩j=1~N [D(Qj)∩D(Pj)] かつ QjD⊂D, PjD⊂D
(ii) {Qj,Pj}j=1~N はD上でCCRを満たす。
(iii) 各Qj, PjはD上で本質的に自己共役である。
参照:ヴァイル型表現については新井先生の論文「Construction of a Weyl Representation from a Weak Weyl Representation of the Canonical Commutation Relation (2008)」(PDF)の「Introduction」の箇所を参照。
この定理によって、各自由度ごとにヴァイル型表現の全体はCCRの自己共役表現の全体の部分集合であることがわかる。だが、CCRの自己共役表現の中には次のようにヴァイル型でないものもある。
対称表現 ⊂ 自己共役表現 ⊂ ヴァイル型表現
ここまではとても難しく、もう一度読みなおしたが僕の理解度は6割止まり。ギブアップしようかという考えが何度か頭をよぎった。これに続く物理現象とのかかわりについての部分がなかったら、おそらく僕は投げ出していただろう。
電子などの荷電粒子が磁場の中を運動するとローレンツ力によってその進路が曲げられることは電磁気学で学ぶ。ところが磁場と離れた場所でも電子波の位相に影響を及ぼすことがあることが1959年に予言され、1986年に外村彰により電子線ホログラフィーの手法を用いて、その存在が実証された。(参照用PDF)これが「アハラノフ-ボーム効果」と呼ばれる古典電磁気学では説明のつかない量子力学的現象である。
参考書籍
「量子力学を見る―電子線ホログラフィーの挑戦:外村彰 」
「電子波で見る世界―電子線ホログラフィー:外村彰」
第3章の「CCRの非同値表現とアハラノフ-ボーム効果」という節では、磁場のある系の物理的運動量が本質的自己共役性を持つことを示すことから始まる。
古典電磁気学で学ぶように磁場BはベクトルポテンシャルAによって記述される。この章のモデルとして磁場としてはN個の特異点にデルタ関数的に集中している極めて特異な場合について想定している。
この条件で、まず物理的運動量作用素が本質的に自己共役であることが証明され、磁場が存在する状況において量子力学的粒子(荷電粒子)が「歪み」をうけながら磁気的並進をすることが導かれる。
またベクトルポテンシャルAのジョルダン閉曲線Cに沿う線積分によって、この閉曲線Cの内部を貫く磁束をヴァイル型の交換関係によって示すことができる。
さらにあるクラスのベクトルポテンシャルAに対して、位置作用素と物理的運動量の組は(自由度2の)CCR表現になり、これが満たされるための必要条件はAが「平坦」であることが導けるのだ。
すなわち、もともと磁場はN個の点に集中して存在すると想定したわけであるから、これらの特異点以外でもベクトルポテンシャルAは「平坦」に存在し、その結果、特異点以外のところでも荷電粒子に影響を及ぼす電磁ポテンシャルが存在することが示される。(アハラノフ-ボーム効果)
アハラノフ-ボーム効果:
http://dolphin.phys.s.u-tokyo.ac.jp/research/sc2des/ws/ab.html
量子力学においては、物質と電磁場の相互作用を第一義的に決めるのは、電磁場そのものではなく、それを生み出す電磁ポテンシャルAであるからだ。電磁ポテンシャルは磁場が局在していても、磁場の局在領域を超えて存在しうるので、磁場を通過しない電子とも相互作用を行うことが可能なのである。
電子波で見る電磁界分布【ベクトルポテンシャルを感じる電子波】外村 彰
http://www.ieice.org/jpn/books/kaishikiji/200012/20001201-1.html
次に論じられるのは、ここで用いたCCRの表現が、シュレーディンガー表現と同値なものかどうかを決定することだ。結果的としてCCRの表現が同値であるためにはCCR表現が「既約」であり、「磁束が局所的に量子化」されていることが必要十分条件であることが導かれる。(その証明には磁束について成り立つ「ヴァイルの交換関係」と「フォン・ノイマンの定理」が用いられている。)
そしてCCRの表現がシュレーディンガー表現と同値でない場合についても、アハラノフ-ボーム効果が生じることが証明されるのだ。それはこの効果自体は純粋に幾何学的、トポロジカルなものであって、系の力学の詳細(ハミルトニアンの形)には依存していないことを意味している。
節の最後に「弱ヴァイル型表現」というものを導入する。(前述の新井先生の論文PDFを参照。)
ヴァイル型表現 ⇒ 弱ヴァイル型表現
弱ヴァイル型表現 + 稠密性条件 ⇒ 対称表現
という関係が成り立っている。
次の節では「時間作用素T」を導入し、ハミルトニアン作用素Hとの間に成り立つ関係を調べる。物理の教科書ではあまり取り扱われることのない「時間とエネルギーに関する不確定性関係」に内在する数学的構造を明らかにするのだ。
詳細は割愛するが、まず「弱時間作用素T」を定義しエネルギー(ハミルトニアン作用素H)との間の不確定性関係を導く。実はこの弱時間作用素はHが下に有界ならば本質的に自己共役ではないことが証明されるのだ。ということは弱時間作用素は物理量ではなくなってしまうわけなのだが、物理的に意味がない存在ということにはならない。
系の時間発展はユニタリー群が統制し、素粒子の生成・消滅は生成・消滅作用素が司っているように、自己共役作用素も物理現象の現出に何らかの役割を果たしているのだ。作用素の空間には、物理現象の現出との関連においても、ある種の(無限)階層的構造が存在し、各作用素はそれぞれ固有の役割を担っているのである。
次の「CCRの表現と弱時間作用素」という節では自由度が1でハミルトニアンが簡単な場合について、
A)非相対論的な場合、
B)相対論的場合(1)-ハミルトニアンのCCRがシュレーディンガー型表現、
C)相対論的場合(2)-ハミルトニアンのCCRがディラック型表現
のタイプのときに、それぞれ弱時間作用素とハミルトニアン作用素が、量子現象の状態のヒルベルト空間を表現空間とするCCRの自己共役表現 {H, D, {Qj,Pj}j=1~N} から作られることを具体的な計算で示している。
章の最後から2番目の節では「強時間作用素」に対してもエネルギーと時間の間の不確定性関係が成立していることが述べられている。(証明は省略されている。)
読後の感想を言わせていただければ「アハラノフ-ボーム効果」や「時間とエネルギーに関する不確定性関係」のようにシンプルな物理現象であったとしても、その背後には恐ろしく複雑な数学構造が潜んでいるのだなということ。数学構造が複雑なだけでなく、その証明も僕には手ごわかった。
このように、非常に深く込み入った内容であったため読むのに時間がかかってしまった。引き続き第4章「量子力学における対称性」に取り組むことにしよう。
「量子力学の数学的構造 I:新井朝雄、江沢洋」
「量子力学の数学的構造 II:新井朝雄、江沢洋」
「量子現象の数理:新井朝雄」



応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。




関連記事:
ヒルベルト空間論:保江邦夫
https://blog.goo.ne.jp/ktonegaw/e/72859f8fd3f37367cb8e27895a5f9341
ヒルベルト空間と量子力学:新井朝雄
https://blog.goo.ne.jp/ktonegaw/e/fa4d9da634afbdb8a9dfc1ac162f7afe
量子力学の数学的構造 I:新井朝雄、江沢洋
https://blog.goo.ne.jp/ktonegaw/e/196b59dc50fca361ba523036e7eeb908
量子力学の数学的構造 II:新井朝雄、江沢洋
https://blog.goo.ne.jp/ktonegaw/e/a4ef01e94a8c0384cec353ebe4d542e4
「量子現象の数理:新井朝雄」
章立て
第1章:物理量の共立性に関わる数理
第2章:物理量の自己共役性
第3章:正準交換関係の表現と物理
第4章:量子力学における対称性
第5章:物理量の摂動と固有値の安定性
第6章:物理量のスペクトル
第7章:散乱理論
第8章:虚数時間と汎関数積分の方法
第9章:超対称的量子力学
(全体の章立ては記事のいちばん下を参照。全体の詳細な目次はこのページを参照。)
第3章:正準交換関係の表現と物理
- はじめに
- 予備的考察
- ヴァイル型表現
- シュレーディンガー表現のヴァイル型性
- ヴァイル型表現の構造 - フォン・ノイマンの一意性定理
- CCRの非同値表現とアハラノフ-ボーム効果
- 弱ヴァイル型表現
- 時間作用素
ノート
演習問題
関連図書
第3章の内容は冒頭で次のように要約されている。
量子力学の根本原理の一つである、代数構造としての正準交換関係(CCR: Canonical Commutation Relation)の表現論の初等的部分を、量子物理との関連を念頭に置きつつ論述する。また、CCRの変形から定義される時間作用素の概念についてもふれる。これは従来曖昧に論じられてきた”時間-エネルギーの不確定性関係”に対する一つの明晰な形を与える。さらに、時間作用素と状態の時間発展(生き残り確率)との関係について議論する。
ハイゼンベルクの不確定性関係を考慮すると、量子的粒子の粒子的描像における位置作用素Qと運動量作用素Pは次のような正準交換関係(CCR)に従うことは「量子力学の数学的構造 II:新井朝雄、江沢洋」で説明されている。
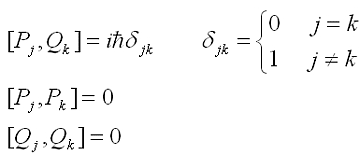
さらに外的自由度に関する限り、有限自由度の場合と無限自由度の場合も含めて量子力学は代数構造としてのCCRのヒルベルト空間表現として捉えられることも示された。有限自由度の量子力学と量子場の理論のような無限自由度の量子力学との違いは、有限自由度のCCRの表現と無限自由度のCCRの表現の違いとして把握される。
無数に存在するCCRの表現を解析することによって、量子現象があらわれる仕方を根本で支配する数学構造のひとつの相を根源から明晰に認識することが可能になるはずだ。そのためには無数にあるCCRの表現たちを本質的に異なるものとそうでないものとに分類、整理することが必要である。
シュレーディンガー表現のCCRとボルン-ハイゼンベルク-ヨルダン表現のCCR(参照ページ)が、表現形式が異なっていても、物理的にはまったく同じ内容を記述するものがあり、そのような表現どうしは物理的に同値であるという。他方、ある表現は別の表現と本質的に異なる物理的内容を内蔵している場合がある。このような二つの表現は物理的に非同値であるという。
この第3章では有限自由度のCCRの表現に限定して考察されている。つまり量子場の理論は含まれない。以下、表現の既約性、シュレーディンガー表現の既約性、表現の同値性、ヴァイル型表現、ヴァイル型表現の既約性、シュレーディンガー表現のヴァイル型性、ヴァイル型表現の構造が一意であること(フォン・ノイマンの一意性定理)、フォン・ノイマンの一意性定理からの帰結など数学としての説明とそれらの証明が25ページに渡って展開されている。
注意:ヴァイル(Weyl)の一般的な表記は「ワイル」だが、この記事では本書での表記に従って「ヴァイル」とした。
フォン・ノイマンの一意性定理からの帰結とは次のとおり。
Hを可分なヒルベルト空間、H上の自己共役作用素の組 {Qj,Pj}j=1~N はCCRのヴァイル型表現であるとする。このとき次の(i)~(iii)が成り立つような稠密な部分空間 D⊂H が存在する。
(i) 各Qj, PjはDを不変にする:D⊂∩j=1~N [D(Qj)∩D(Pj)] かつ QjD⊂D, PjD⊂D
(ii) {Qj,Pj}j=1~N はD上でCCRを満たす。
(iii) 各Qj, PjはD上で本質的に自己共役である。
参照:ヴァイル型表現については新井先生の論文「Construction of a Weyl Representation from a Weak Weyl Representation of the Canonical Commutation Relation (2008)」(PDF)の「Introduction」の箇所を参照。
この定理によって、各自由度ごとにヴァイル型表現の全体はCCRの自己共役表現の全体の部分集合であることがわかる。だが、CCRの自己共役表現の中には次のようにヴァイル型でないものもある。
対称表現 ⊂ 自己共役表現 ⊂ ヴァイル型表現
ここまではとても難しく、もう一度読みなおしたが僕の理解度は6割止まり。ギブアップしようかという考えが何度か頭をよぎった。これに続く物理現象とのかかわりについての部分がなかったら、おそらく僕は投げ出していただろう。
電子などの荷電粒子が磁場の中を運動するとローレンツ力によってその進路が曲げられることは電磁気学で学ぶ。ところが磁場と離れた場所でも電子波の位相に影響を及ぼすことがあることが1959年に予言され、1986年に外村彰により電子線ホログラフィーの手法を用いて、その存在が実証された。(参照用PDF)これが「アハラノフ-ボーム効果」と呼ばれる古典電磁気学では説明のつかない量子力学的現象である。
参考書籍
「量子力学を見る―電子線ホログラフィーの挑戦:外村彰 」
「電子波で見る世界―電子線ホログラフィー:外村彰」
第3章の「CCRの非同値表現とアハラノフ-ボーム効果」という節では、磁場のある系の物理的運動量が本質的自己共役性を持つことを示すことから始まる。
古典電磁気学で学ぶように磁場BはベクトルポテンシャルAによって記述される。この章のモデルとして磁場としてはN個の特異点にデルタ関数的に集中している極めて特異な場合について想定している。
この条件で、まず物理的運動量作用素が本質的に自己共役であることが証明され、磁場が存在する状況において量子力学的粒子(荷電粒子)が「歪み」をうけながら磁気的並進をすることが導かれる。
またベクトルポテンシャルAのジョルダン閉曲線Cに沿う線積分によって、この閉曲線Cの内部を貫く磁束をヴァイル型の交換関係によって示すことができる。
さらにあるクラスのベクトルポテンシャルAに対して、位置作用素と物理的運動量の組は(自由度2の)CCR表現になり、これが満たされるための必要条件はAが「平坦」であることが導けるのだ。
すなわち、もともと磁場はN個の点に集中して存在すると想定したわけであるから、これらの特異点以外でもベクトルポテンシャルAは「平坦」に存在し、その結果、特異点以外のところでも荷電粒子に影響を及ぼす電磁ポテンシャルが存在することが示される。(アハラノフ-ボーム効果)
アハラノフ-ボーム効果:
http://dolphin.phys.s.u-tokyo.ac.jp/research/sc2des/ws/ab.html
量子力学においては、物質と電磁場の相互作用を第一義的に決めるのは、電磁場そのものではなく、それを生み出す電磁ポテンシャルAであるからだ。電磁ポテンシャルは磁場が局在していても、磁場の局在領域を超えて存在しうるので、磁場を通過しない電子とも相互作用を行うことが可能なのである。
電子波で見る電磁界分布【ベクトルポテンシャルを感じる電子波】外村 彰
http://www.ieice.org/jpn/books/kaishikiji/200012/20001201-1.html
次に論じられるのは、ここで用いたCCRの表現が、シュレーディンガー表現と同値なものかどうかを決定することだ。結果的としてCCRの表現が同値であるためにはCCR表現が「既約」であり、「磁束が局所的に量子化」されていることが必要十分条件であることが導かれる。(その証明には磁束について成り立つ「ヴァイルの交換関係」と「フォン・ノイマンの定理」が用いられている。)
そしてCCRの表現がシュレーディンガー表現と同値でない場合についても、アハラノフ-ボーム効果が生じることが証明されるのだ。それはこの効果自体は純粋に幾何学的、トポロジカルなものであって、系の力学の詳細(ハミルトニアンの形)には依存していないことを意味している。
節の最後に「弱ヴァイル型表現」というものを導入する。(前述の新井先生の論文PDFを参照。)
ヴァイル型表現 ⇒ 弱ヴァイル型表現
弱ヴァイル型表現 + 稠密性条件 ⇒ 対称表現
という関係が成り立っている。
次の節では「時間作用素T」を導入し、ハミルトニアン作用素Hとの間に成り立つ関係を調べる。物理の教科書ではあまり取り扱われることのない「時間とエネルギーに関する不確定性関係」に内在する数学的構造を明らかにするのだ。
詳細は割愛するが、まず「弱時間作用素T」を定義しエネルギー(ハミルトニアン作用素H)との間の不確定性関係を導く。実はこの弱時間作用素はHが下に有界ならば本質的に自己共役ではないことが証明されるのだ。ということは弱時間作用素は物理量ではなくなってしまうわけなのだが、物理的に意味がない存在ということにはならない。
系の時間発展はユニタリー群が統制し、素粒子の生成・消滅は生成・消滅作用素が司っているように、自己共役作用素も物理現象の現出に何らかの役割を果たしているのだ。作用素の空間には、物理現象の現出との関連においても、ある種の(無限)階層的構造が存在し、各作用素はそれぞれ固有の役割を担っているのである。
次の「CCRの表現と弱時間作用素」という節では自由度が1でハミルトニアンが簡単な場合について、
A)非相対論的な場合、
B)相対論的場合(1)-ハミルトニアンのCCRがシュレーディンガー型表現、
C)相対論的場合(2)-ハミルトニアンのCCRがディラック型表現
のタイプのときに、それぞれ弱時間作用素とハミルトニアン作用素が、量子現象の状態のヒルベルト空間を表現空間とするCCRの自己共役表現 {H, D, {Qj,Pj}j=1~N} から作られることを具体的な計算で示している。
章の最後から2番目の節では「強時間作用素」に対してもエネルギーと時間の間の不確定性関係が成立していることが述べられている。(証明は省略されている。)
読後の感想を言わせていただければ「アハラノフ-ボーム効果」や「時間とエネルギーに関する不確定性関係」のようにシンプルな物理現象であったとしても、その背後には恐ろしく複雑な数学構造が潜んでいるのだなということ。数学構造が複雑なだけでなく、その証明も僕には手ごわかった。
このように、非常に深く込み入った内容であったため読むのに時間がかかってしまった。引き続き第4章「量子力学における対称性」に取り組むことにしよう。
「量子力学の数学的構造 I:新井朝雄、江沢洋」
「量子力学の数学的構造 II:新井朝雄、江沢洋」
「量子現象の数理:新井朝雄」



応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。

関連記事:
ヒルベルト空間論:保江邦夫
https://blog.goo.ne.jp/ktonegaw/e/72859f8fd3f37367cb8e27895a5f9341
ヒルベルト空間と量子力学:新井朝雄
https://blog.goo.ne.jp/ktonegaw/e/fa4d9da634afbdb8a9dfc1ac162f7afe
量子力学の数学的構造 I:新井朝雄、江沢洋
https://blog.goo.ne.jp/ktonegaw/e/196b59dc50fca361ba523036e7eeb908
量子力学の数学的構造 II:新井朝雄、江沢洋
https://blog.goo.ne.jp/ktonegaw/e/a4ef01e94a8c0384cec353ebe4d542e4
「量子現象の数理:新井朝雄」
章立て
第1章:物理量の共立性に関わる数理
第2章:物理量の自己共役性
第3章:正準交換関係の表現と物理
第4章:量子力学における対称性
第5章:物理量の摂動と固有値の安定性
第6章:物理量のスペクトル
第7章:散乱理論
第8章:虚数時間と汎関数積分の方法
第9章:超対称的量子力学























http://eman.hobby-site.com/bbs/past/log08961.html
や
http://eman.hobby-site.com/bbs/past/log08963.html
の「あ」さんのコメントが明快です。
ありがとうございます!
じっくり勉強させていただきますね。