掲載画像: 地球と重力、放物線と楕円のグラフ
「ボールを投げると地球の重力によって軌跡は放物線を描く。」と高校の物理で習う。(中学の理科だっけな?)けれどもこれは本当の意味では正しくない。空気抵抗を考えていないからというのも1つの答なのだが、この記事では(月面など)空気がない理想的なケースについての話。
放物運動を勉強してから数ヶ月後、惑星の運動の単元でケプラーの法則のところで「惑星は太陽を焦点とする楕円軌道上を動く。」と教えてもらうのだが、ボールの軌跡が放物線を描くことと、惑星の軌跡が楕円軌道を描くことが矛盾しているのにみなさんは気がついただろうか?
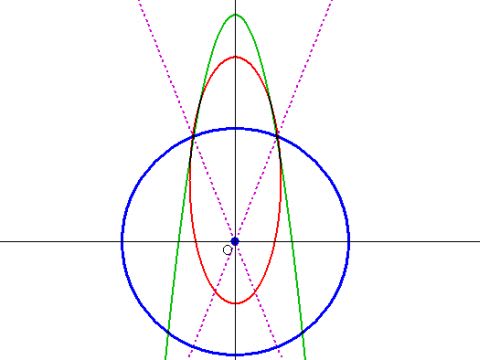
掲載画像の青い円は地球の表面で、緑線は地上から投げたボールの軌跡(放物線)を、そして赤線はボールを地球の衛星と見立てた場合の楕円軌道を描いたものだ。紫色の点線はそれぞれボールを投げ上げた点と落下点での重力の方向をあらわしている。(放物線や楕円は地球の内部にも描かれているが、実際は地面にぶつかってしまうので、想像上で延長した曲線と考えてもらいたい。)すると、ボールと地球の関係は月と地球の関係と同じで、惑星と太陽の関係とも同じと考えられる。
そう、ボールの軌跡は放物線ではなく楕円の一部であるはずなのだ。
物理の授業で軌跡が放物線になると教えるのは、投げ上げた地点と落下点が地球のサイズに対して比較にならないくらい近いからで、投げ上げた地点と落下点での重力が同じように真下を向いていると仮定しているからだ。つまり地面が完全に平面だと仮定しているわけだ。この場合は確かに教科書に書いてあるとおり放物線になる。
しかし、厳密に言えば地面は平面ではなく球の一部だ。投げ上げた点と落下点での重力の方向はわずかにずれているし、ボールが飛ぶにしたがって時々刻々重力の方向は変化する。重力は常に地球の中心に向いているからだ。この場合、惑星の運動と同じようにボールの軌跡は楕円を描く。つまり「放物線」は近似した曲線にすぎない。
ちなみに、ここまではニュートン力学(古典力学)で解ける範囲だ。
テストの回答にボールの軌跡は「楕円」である、と答えたら正解にはもらえない。近似にすぎないと知っていても、回答用紙には「放物線」と書かなければならない。学校の先生は放物線ではないことを本当は知っているのかもしれないが、生徒を混乱させないためとか、学習指導要領では放物線として教えることが決められてるからとか、実生活では放物線で近似しても誤差は無視できるほど小さいとか、実際には地表の空気抵抗があるからとか、いろいろな理由をつけて真実を隠しているのだ。
さらに厳密に言えば、楕円軌道ですら近似であって、本当の意味では正しい答ではない。
アインシュタインの一般相対性理論(重力によって空間が歪むという理論)からの重力方程式を解くと、惑星の運動は楕円ではなく公転するたびに次の図のように軌道がずれていく。これを「歳差運動」という。1周回って同じ場所に戻ってこないのだから軌跡は楕円とは言えない。(楕円モドキ?)
後日訂正:歳差運動自体は複数の他の惑星によって惑星の楕円軌道がずれていくもので一般相対性理論による原因でおこるものではない。一般相対性理論から導かれるのは歳差運動自体が、本来ニュートン力学で計算される歳差運動と少しずつずれていくということなのだ。もし、他の惑星が存在しない場合、歳差運動は一般相対性理論によるわずかな影響だけが観測されるはずである。
つまり、ボールにも地球にも質量があり、わずかではあるが周囲の空間を歪めているので一般相対性理論の重力方程式に従って運動するからだ。これを解くためにはこのような方程式を解かなければならないのだが、計算すると正確に楕円軌道を描いているわけではないことがわかる。
時間をとってみても教科書には書かれていないことがある。ボールは頂点に近づくにつれて速度が小さくなるので、地面に近いときよりも時間は早く進んでいるはずだ。これは「物体の速度が速いほど時間は遅れる。」という特殊相対性理論から簡単に導くことができる。また、速度が時間に影響するだけでなく重力も時間に影響を与える。一般相対性理論では「重力により時間が遅れる。」からだ。ボールの軌道の頂点は投げ上げた地点より地球の中心からの距離が遠いから、時間は早く進むはずだ。このように時間は速度と重力の両方に影響を受けるので事態はいっそう複雑になる。最終的にはやはり重力方程式をコンピュータで計算しないと実際にボールが描く「楕円モドキの軌跡」は得られない。
そんな細かいことを気にしなくても。。。という声が聞こえてきそうだが、相対性理論によるこのわずかな影響を計算に入れないとカーナビの精度が10メートル以上ずれてしまうのだ。細かい違いではあるけれども、精度が求められる世界ではあなどれないものだということがよくわかる。
ものごとの本質が深く理解されるにつれて物理現象の「近似」は限りなく真実の姿に近づいていく。ボールの放物運動はその格好の例といえよう。
?
この話の続き、つまり重力や重心、質点などについての考察については「僕が物理と数学にハマリだしたきっかけ - 重心と質点の話」から始まる一連の記事や「理科復活プロジェクト始動!」という記事をお読みいただきたい。?
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。?
?


























確かに、投げたボールの軌跡は、普通の放物線ではありませんね。
でも、良く日本語をかみしめてみると、別の味もします。というのは、岩波の物理入門コースの1巻の「力学」の最後に出てくる「ナイルの放物線」という言葉。
地球が自転しているために、真下に落としたはずのものが、真下に落ちない。という効果を考慮して求めた曲線を、「ナイルの放物線」といいますよね。でも、これって、放物線じゃないんですよね。
私も初め意味が分からなかったのですが、良く考えてみると、「放った物体のえがく線=放物線」という、日本語の基本に返ると、正しいんです。
だから、投げたボールの描く曲線は、やっぱり、放物線なんですよね。
高校の先生が、ここまで考えているかどうかは分かりませんが・・・
こちらこそお久しぶりです。ていねいなコメントありがとうございます。
地球の自転の影響を考えると「ガリレイ変換」の影響で、もっと複雑なことになりますね。自転の方向とボールを投げる方向によっても変わってきますし。
> 「放った物体のえがく線=放物線」という、
> 日本語の基本に返ると、正しいんです。
あはは!そうですね!国語的には放物線なのだから!英語だとparabola(パラボラ)とかparabolicになるのでこちらの言語だと「物を投げた軌跡」の意味はない事に。。。
> 高校の先生が、ここまで考えているか
> どうかは分かりませんが・・・
最近の高校生をとりまく状況を想像してみるに、先生方もとてもそこまで踏み込んだ授業をしたり、考えたりする余裕がないように思えます。
EROICAさんもご存知のようにニュートン力学にしたって、とても深い意味を持っているわけなのですけどね。その甘い果実を味わえる人は、本当にそうなのかと常に疑問を持っていられる人に限られるのだと思います。