僕が物理と数学にハマリだしたきっかけ - 重心と質点の話

中学生のころから天文や数学は好きだったが、僕が物理や数学の本当の魅力に気がついたのは高校の物理の授業が原因だった。

ニュートンの万有引力についての授業ではいきなり「天体の全質量は質点に集中している」として次の万有引力の公式が紹介される。



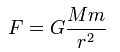
「物理って何ていいかげんなんだろう。」と僕は思った。



この図で r をものすごく長くとったときのように天体が夜空の星のように点としてみなせるほど遠くに引き離した場合だったら、質点の仮定は「近似」として許せる。しかし下の図のように片一方がとても大きく、天体どうしが近い場合にに大きいほうの質量が中心に集中しているなどとしてよいものだろうか？



それは僕にとって「梅干を丸呑みしろ」と言われるに等しいことだった。さらにその質点は天体（物体）の質量重心の位置にあるというのだ。幾何学的な中心と重心は一般的には違うのに。

物体どうしがそれぞれ距離の２乗に反比例する大きさの力で引き合うというのは認めたとしても、距離と力の方向をはかる基準を質点に置くというのが解せなかった。基準にする点はどこかに設けなければいけないのはわかるが、それが重心だとするのも早計だし地球がほぼ球対称だから中心を基準とせよというのも安直だ。それこそ「蛮勇引力」の法則だ。（この駄洒落はたまたま漢字変換で表示されたので、いつか使ってやろうと思っていた。）

物体どうしがその質量によって引き合うならば、物体を構成する微小部分どうしが引き合い、それぞれの部分の合計の力で引き合っていることになる。地球上にいる自分を例にとれば、足元の地面も自分を引き寄せているし、地球の反対側のブラジルの地面もものすごく小さい力ながら自分を引っ張っている。

アメリカやフランスの地面も日本にいる自分を斜め下方向へ引っ張って引力に貢献しているはずだ。そのような地球上のあらゆる場所、地球の内部のマントルや核も含めて自分を引っ張る力をすべて合計したものが、今自分が足に感じている地球の引力になるという理屈。いろいろな方向にわずかずつの力で引っ張られているはずなのだが、私たちはいろいろな方向に引かれているようには感じない。それらは方向も含めて総合計され、ただ真下の１方向にだけ引かれていると感じるのが引力だ。

この引力は次のように地球を「無限個に」分割した微小体積要素にその部分の質量密度を掛け算し、自分から微小体積要素までの距離の２乗で割る。そして球全体で合計すれば引力は理論的には求まるはずだ。図で自分はPの位置にいるとする。



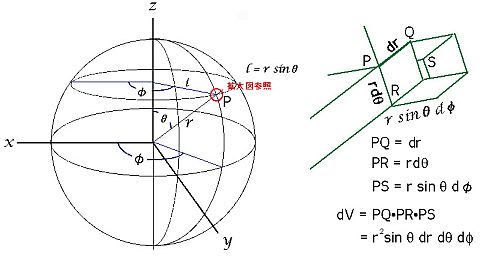
実際の計算は３次元の極座標と３重積分を使うことになるので高校レベルの数学では難しいが引力の方向と大きさを求めることができるはずだ。３次元の極座標とはこのような座標系のこと。僕はこの計算で得られる引力と質点を球の中心に置いた場合の引力の計算結果が（方向と大きさの両方について）同じになるとはにわかに信じられなかったのだ。３重積分を使う実際の計算式はこちらの記事でご覧いただける。

今だったらパソコンでシミュレーションして求めることもできるはずだ。その場合は直交座標を使ったほうがプログラムは簡単だ。地球を下の図のようにたくさんの微小な立方体に分割し、それぞれの微小立方体からの引力の影響を自分からの距離による減少の割合と方向を考慮に入れた上ですべて足し合わせればよい。赤い点が地球上の自分の位置だと考える。微小立方体を小さくすればするほど引力の計算精度は上がるはずだ。



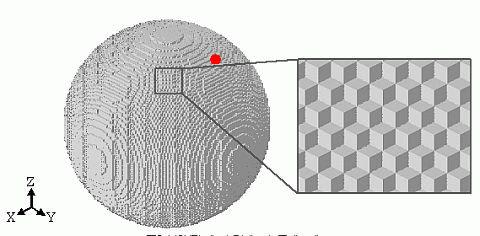
しかし待てよ。自分が地表にいたとしたら地面の微小体積要素からの距離はゼロになって引力が無限大に発散してしまう。本当にこの方法で地球全体の微小引力の総和を計算できるのだろうか？


もやもやとしながら僕は考え続けた。そして下のような「やじろべえ」を思い浮かべながら物の重心というものについて考えはじめた。



やじろべえの腕についている２つの球の重心はもちろんそれぞれの球の中心にある。けれどもやじろべえ全体をひとつの物体とみなすと、全体の重心は画像の赤い点の位置にあることに気づく。

重心という物理的実体が何もないものが空間に浮かんでいるのが不思議だった。そしてやじろべえを支えている支点から重心に頭の中で（黄色い）線を引くと、まさにこれは「振り子」になることを僕は確信した。やじろべえの２つの玉の質量がこの重心に集中して見えない２倍の重さの玉となり、振り子を作っているのが僕には見えた。

やじろべえの回転方向は別にして、前後左右の揺れについては２つの玉の質量重心の位置に質量が２倍の玉を吊るした振り子と同じような力学的状態だと気がついたわけだ。

玉の質量が違う場合でも、それらの重心の位置を計算するのは簡単だ。



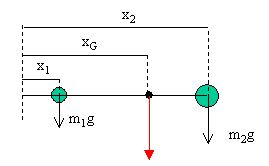
この図のような場合、重心の位置は次のような計算式で求められる。



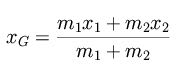
玉の数がｎ個に増えても、この計算式は容易に一般化できる。Σは総和を表す数学記号だ。



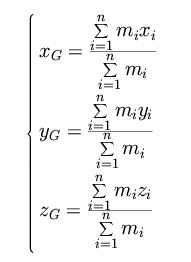
ｎ個の玉が直線上に並んでいず、空間に散らばっている場合でもこのように重心の３次元座標を計算できる。１次元から３次元への拡張だ。これは「力」がｘ、ｙ、ｚ成分に線形性を保ちながら分解できることを意味している。



つまり図示するとこのようになる。赤い玉すべてのの質量重心はGという黄色の点にある。（赤玉どうしの相対的な位置関係が固定していると考えるのが前提だ。）



上の３つの計算式はベクトルの足し算として１つの式にまとめることができる。もちろん力の重ね合わせに線形性が完全に保証されていることが事実の根底にあるのは間違いない。



さらに玉の数を増やしてお互いがくっつくようにすれば「物体」をつくることができる。そしてくっつけ方によってどんな形の物体も作ることができる。玉と玉がしまいに連続したひとつの物体になると考えると、その物体の重心の位置は次の式のように積分記号∫を使ってあらわされる。この場合の積分とは連続した無限小の要素 dV を領域 V のすべてにわたって足し合わせる∫計算のことだ。



ρが物体の質量密度、M が物体全体の質量だ。dV というところは物体を分割した微小部分の体積で、r は微小要素の位置、rc は物体の重心の位置をベクトルで表したものだ。

この段階で僕はその物体が「どんな形でもよくなっていること」に気がついた。すごいと思った。物体がどんな形であっても重心の位置はこんなにシンプルな式で表現されることに僕は驚嘆した。高校３年のときのことだ。この式は地球がジャガイモのようにいびつな形をしていたとしても重心の位置はこの式で計算できることを意味している。

「やじろべえ」の重心が見えない振り子の質点であることを認めると、力のベクトルの重ね合わせに線形性が保証されている限り、上のような連続物体に働く力学的な作用の「中心」の位置が質量重心の位置と一致することが論理的に矛盾なく導かれているようにも思える。しかしこれは重心を求めただけにすぎないのであって、それを引力の中心＝質点と同一視してよいのだろうか？また引力が無限大に発散しないかということについての疑問も残っている。これについての検証は完了していない。

このような感じで僕が物理や数学に魅せられていったのだ。上記の考察を踏まえた上で以下の法則を読みなおすと、その深い意味にあらためて謎が深まる。２）は「定理」であって検証された法則ではないのだ。

=====================================================
１）任意の質量分布による万有引力質点の集合とみなしてそれらによる万有引力を重ね合わせたものに等しい。(重ね合わせの原理)

２）有用な定理：有限な大きさをもつ総質量M の球形の物体があり、その内部の密度分布が球の中心の周りで対称(球対称) とする。このときこの物体が外部にある別の質点に及ぼす重力や重力ポテンシャルは、球の中心に質量M の質点を置いた場合に得られるものと等しい。
=====================================================


なお、この話には続きがある。万有引力の公式からさらに計算を進めることによって、ニュートンの重力ポテンシャルψは次のような「ポアッソン方程式」と呼ばれる偏微分方程式の形で書き表すこともできるのだ。数式ってすごい。ポアッソン方程式の具体的なイメージを知りたい方はこのページをご覧になるとよい。



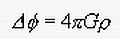
そこに至る計算過程はこのページでご覧いただけるのでご一読いただきたい。さらに数式の魅力にとりつかれることだろう。

このように重力ポテンシャルをポアッソン方程式のような「微分形」として記述することはニュートンから230年後、重力が瞬間的に伝わる遠隔力ではなく有限の速度で伝わる近接力であるという重力場の理論をアインシュタインが発見するきっかけとなった。そのあたりのことはこの論文の§５やこの論文の§１６、そしてこの論文の§１で説明している。どれもアインシュタインが重力ポテンシャルのポアッソン方程式をどのように一般相対性理論に応用したかについて述べている箇所だ。

このほかにも多くの物理現象の根底に線形性が保証されていることの重要性について、そして線形性という性質がもしなかったら物理学や数学はおそらく発展しなかっただろうということについては、また今度別の記事で紹介することにしよう。

また自分と地表の距離がゼロであるのに引力の大きさが無限大にならず、地球の自分に対する引力が有限であることについては、後日また考察してみようと思う。無限大の発散については電子のくりこみ理論を見つけた朝永先生のお顔がちらつくが、たしか重力のくりこみ理論は失敗してしまったはずだし、これはまだ発見されていない重力子についての理論だったわけで。。。う～む、謎は深まる。

この話は次の記事に続く。


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。