
「量子波のダイナミクス - ファインマン形式による量子力学 -:森藤正人」
あけましておめでとうございます。
新年最初の記事はkafukaさんから紹介いただいた本書の紹介。僕にとっては経路積分の入門書という位置づけだ。文字も適度に大きく210ページほどの手ごろな分量。(その割に3,360円もする。)2005年の暮れに出版された新しい本である。
この本の主役は「電子」だ。rikunoraさんの「電子のカタチ」という記事でご覧いただけるように電子は複素数の「電子波」として運動している。量子力学のいくつかのテーマに対して経路積分の手法を適用し、この電子波がどのような姿で空間に存在し、どのような挙動をしているのかを明らかにしていく。本書の裏表紙には次のように書かれている。
---------
「電子は動く波である」という視点に立って書かれた量子力学の教科書。多くの量子力学の本がシュレーディンガー方程式の定常解(固有値・固有関数)を求めることに主眼を置いているのとは異なり、本書は経路積分法に基づいた独自の観点から電子波の意味を問い直し論じる。
理工系の学部上級生から大学院で、量子力学の意味するところが良く分からなかった人、もっと深い理解を求める人、さらには量子情報、ナノサイエンスといった先進的な分野を切り開こうという人にも勧めたい一冊である。
---------
実際に読んでみたところ経路積分の入門としては「量子力学と経路積分:R.P.ファインマン、A.R.ヒッブス」よりも本書のほうが断然やさしい。ファインマン信奉者の僕としては前者が好きだという事実は曲げられないが、何せ出版されたのが1965年だということ、日本語版には(翻訳の元になった英語版から引きずっている)数式の誤植が800箇所以上もあること、応用例が初学者には難し過ぎることを考え合わせれば、手軽に学べるのが本書のほうであると言わざるを得ない。更に本書で取り上げられている解説はシンプルで、計算の難しさもほどほどに抑えてあるのがよい。本家ファインマン&ヒッブス本が優れているのは経路積分の原理を解説した前半部分である。
経路積分の原理の解説について、本書では古典力学としての熱の拡散、ブラウン運動を記述する微分方程式を変形して得られる積分方程式と量子力学のシュレーディンガーの波動方程式から変形して得られる積分方程式の類似性を紹介し、二つの積分方程式の積分核がそれぞれ熱核、(量子力学の)経路積分におけるファインマン核であることを示す。方程式の類似性からわかるように古典力学および量子力学における2つの状態は拡散していくことを意味している。自由粒子としての電子波(複素数波)も熱のように移動しながら拡散していくのだ。
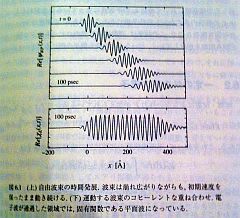
次に面白いと思ったのが電子波のコヒーレント状態のこと。時間の経過に従い移動する電子波を一定時間の間で積分することにより得られる電子波の残像だ。本書全体を通じて数値計算で得られたグラフがたくさん紹介されている。電子波の伝わる様子、トンネル効果やポテンシャルの壁で跳ね返される様子が視覚的に紹介されている。たとえばこんな感じだ。
自由粒子としての電子波の時間発展(クリックで拡大)
第2章には経路積分を統計力学に適用する方法が説明されている。この中にホーキング博士の理論でないにもかかわらず「虚数時間」が登場するのは意外だった。つまり τ=it と置くパターンだ。(τ:虚数時間)これは虚数時間を設けることで経路積分の時間発展演算子 exp(-iHt) が統計力学のボルツマン因子 exp(-Eτ) の形になることを利用して統計力学で経路積分を使えるようにするためだ。実際に時間が虚数であるわけではない。
第4章の調和振動子についての説明は難しかった。事前に場の量子論や第二量子化についてよく理解しておくべきだろう。
その他の章については目次をご覧になって想像していただきたい。どの章も上手にまとめられていて読みやすかった。経路積分はシンプルで大胆なアイデアにもかかわらず現在でも手法が研究、発展を続けている。本書では近年の成果も紹介されているのがよかった。
巻末の付録では経路積分とは密接なつながりのある解析力学とブラ・ケットでの状態ベクトルについて、初学者向けに解説ページを設けている。ディラックのブラ・ケット記法やユニタリー演算子を使った表示の変換について、これ以上やさしく書けないというレベルで説明しているので、他書で理解できなかった方は本書で学ぶとよいだろう。
経路積分の教科書としては2冊目となった本書だが、同じテーマでもう1冊、それもかなりボリュームのある教科書を読んでから次のテーマに進みたいと思っている。
kafukaさん、よい本を紹介していただきありがとうございました。
-------------
2月3日に追記
本書についてkafukaさんが数式を使った解説記事を書いていらっしゃいます。
経路積分こと始め(1)
https://ameblo.jp/kafuka-no-ochan/entry-12511310350.html
-------------
それでは、今年も「とね日記」をよろしくお願いします。
参照ページ:
経路積分とは何か?(Applet同梱版)
http://homepage3.nifty.com/iromono/movingtext/pathintegral1.html
現代物理と仏教を考えるページ
~ファインマンの経路積分量子化と華厳経を中心に~
http://kishi123.server-shared.com/
(僕は仏教については一般常識以上の知識を持ち合わせていないので、物理学と仏教の関係について意見できる立場にはないが、岸さんのこのサイトはファインマンの経路積分を物理学的な側面から詳しく、きちんと解説されているので紹介させていただいた。)
量子力学と経路積分:R.P.ファインマン、A.R.ヒッブス
https://blog.goo.ne.jp/ktonegaw/e/2b9d934a542cf04be54cbede8b16ecde
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。




「量子波のダイナミクス - ファインマン形式による量子力学 -:森藤正人」

目次
第1章:ブラウン運動と確率振幅
- ブラウン運動と熱核
- 確率振幅
第2章:経路積分法
- ファインマン核
- 経路積分1
- 経路積分2
- 波動関数の位相因子とポテンシャル
- 固有関数による展開
- 経路積分とシュレーディンガー方程式
- 虚数時間と統計力学
- 運動量空間でのファインマン核
第3章:WKB近似
- WKB近似
-- 多重積分の実行
-- 古典軌道の安定性と基準モード
-- ゼロ・モードと並進対称性
- ヴァン ヴレック行列式
- WKB近似
- 転回点での波動関数の接続と量子条件
- トンネル効果
第4章:調和振動子および関連する話題
- 量子論における調和振動子
- 振動する波束
- 経路積分による調和振動子の記述
-- 古典運動と作用積分
-- ファインマン核
- 第2量子化と場の量子論
-- 生成・消滅演算子
-- 第2量子化と場の演算子
-- フェルミ粒子
-- 場の量子論におけるグリーン関数
- コヒーレント状態経路積分
-- フェルミ系
第5章:エネルギー表示
- エネルギー表示のファインマン核と状態密度
- 停留位相近似
- 電子波のコヒーレンス:残像という見方
第6章:電子状態の時間発展と自己干渉による固有状態の形成
- 自由粒子
- 一定の外力下の電子
- 調和振動子
-- 離散準位の形成過程
-- 軌道反磁性とランダウ準位
-- シュタルク・ラダー準位
- ヘテロ結合
-- ポテンシャル障壁の透過
第7章:散乱問題における摂動論
- ポテンシャルによる粒子の散乱
- 摂動展開
- リップマン-シュウィンガー方程式
- ボルン近似
-- 諸量の関係
- 摂動問題における半古典近似
- 電子間相互作用
第8章:半古典近似でのダイナミクス
- 電子の軌道と動的WKB近似
- 動的WKB近似の計算例
-- 自由粒子
-- 壁での反射と量子井戸の準位
- トンネル効果とインスタントン
- 共鳴トンネル効果の時間解析
- 多次元空間での運動
付録A:解析力学のまとめ
- 一般化座標とラグランジアン
- 最小作用の原理
- 時間並進対称性とハミルトニアン
付録B:状態ベクトルを用いた表記
- 状態ベクトルを用いた関数の表現
- 変換理論と固有値問題
付録C:公式
参考文献
索引
あけましておめでとうございます。
新年最初の記事はkafukaさんから紹介いただいた本書の紹介。僕にとっては経路積分の入門書という位置づけだ。文字も適度に大きく210ページほどの手ごろな分量。(その割に3,360円もする。)2005年の暮れに出版された新しい本である。
この本の主役は「電子」だ。rikunoraさんの「電子のカタチ」という記事でご覧いただけるように電子は複素数の「電子波」として運動している。量子力学のいくつかのテーマに対して経路積分の手法を適用し、この電子波がどのような姿で空間に存在し、どのような挙動をしているのかを明らかにしていく。本書の裏表紙には次のように書かれている。
---------
「電子は動く波である」という視点に立って書かれた量子力学の教科書。多くの量子力学の本がシュレーディンガー方程式の定常解(固有値・固有関数)を求めることに主眼を置いているのとは異なり、本書は経路積分法に基づいた独自の観点から電子波の意味を問い直し論じる。
理工系の学部上級生から大学院で、量子力学の意味するところが良く分からなかった人、もっと深い理解を求める人、さらには量子情報、ナノサイエンスといった先進的な分野を切り開こうという人にも勧めたい一冊である。
---------
実際に読んでみたところ経路積分の入門としては「量子力学と経路積分:R.P.ファインマン、A.R.ヒッブス」よりも本書のほうが断然やさしい。ファインマン信奉者の僕としては前者が好きだという事実は曲げられないが、何せ出版されたのが1965年だということ、日本語版には(翻訳の元になった英語版から引きずっている)数式の誤植が800箇所以上もあること、応用例が初学者には難し過ぎることを考え合わせれば、手軽に学べるのが本書のほうであると言わざるを得ない。更に本書で取り上げられている解説はシンプルで、計算の難しさもほどほどに抑えてあるのがよい。本家ファインマン&ヒッブス本が優れているのは経路積分の原理を解説した前半部分である。
経路積分の原理の解説について、本書では古典力学としての熱の拡散、ブラウン運動を記述する微分方程式を変形して得られる積分方程式と量子力学のシュレーディンガーの波動方程式から変形して得られる積分方程式の類似性を紹介し、二つの積分方程式の積分核がそれぞれ熱核、(量子力学の)経路積分におけるファインマン核であることを示す。方程式の類似性からわかるように古典力学および量子力学における2つの状態は拡散していくことを意味している。自由粒子としての電子波(複素数波)も熱のように移動しながら拡散していくのだ。
次に面白いと思ったのが電子波のコヒーレント状態のこと。時間の経過に従い移動する電子波を一定時間の間で積分することにより得られる電子波の残像だ。本書全体を通じて数値計算で得られたグラフがたくさん紹介されている。電子波の伝わる様子、トンネル効果やポテンシャルの壁で跳ね返される様子が視覚的に紹介されている。たとえばこんな感じだ。
自由粒子としての電子波の時間発展(クリックで拡大)

第2章には経路積分を統計力学に適用する方法が説明されている。この中にホーキング博士の理論でないにもかかわらず「虚数時間」が登場するのは意外だった。つまり τ=it と置くパターンだ。(τ:虚数時間)これは虚数時間を設けることで経路積分の時間発展演算子 exp(-iHt) が統計力学のボルツマン因子 exp(-Eτ) の形になることを利用して統計力学で経路積分を使えるようにするためだ。実際に時間が虚数であるわけではない。
第4章の調和振動子についての説明は難しかった。事前に場の量子論や第二量子化についてよく理解しておくべきだろう。
その他の章については目次をご覧になって想像していただきたい。どの章も上手にまとめられていて読みやすかった。経路積分はシンプルで大胆なアイデアにもかかわらず現在でも手法が研究、発展を続けている。本書では近年の成果も紹介されているのがよかった。
巻末の付録では経路積分とは密接なつながりのある解析力学とブラ・ケットでの状態ベクトルについて、初学者向けに解説ページを設けている。ディラックのブラ・ケット記法やユニタリー演算子を使った表示の変換について、これ以上やさしく書けないというレベルで説明しているので、他書で理解できなかった方は本書で学ぶとよいだろう。
経路積分の教科書としては2冊目となった本書だが、同じテーマでもう1冊、それもかなりボリュームのある教科書を読んでから次のテーマに進みたいと思っている。
kafukaさん、よい本を紹介していただきありがとうございました。
-------------
2月3日に追記
本書についてkafukaさんが数式を使った解説記事を書いていらっしゃいます。
経路積分こと始め(1)
https://ameblo.jp/kafuka-no-ochan/entry-12511310350.html
-------------
それでは、今年も「とね日記」をよろしくお願いします。
参照ページ:
経路積分とは何か?(Applet同梱版)
http://homepage3.nifty.com/iromono/movingtext/pathintegral1.html
現代物理と仏教を考えるページ
~ファインマンの経路積分量子化と華厳経を中心に~
http://kishi123.server-shared.com/
(僕は仏教については一般常識以上の知識を持ち合わせていないので、物理学と仏教の関係について意見できる立場にはないが、岸さんのこのサイトはファインマンの経路積分を物理学的な側面から詳しく、きちんと解説されているので紹介させていただいた。)
量子力学と経路積分:R.P.ファインマン、A.R.ヒッブス
https://blog.goo.ne.jp/ktonegaw/e/2b9d934a542cf04be54cbede8b16ecde
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。


「量子波のダイナミクス - ファインマン形式による量子力学 -:森藤正人」

目次
第1章:ブラウン運動と確率振幅
- ブラウン運動と熱核
- 確率振幅
第2章:経路積分法
- ファインマン核
- 経路積分1
- 経路積分2
- 波動関数の位相因子とポテンシャル
- 固有関数による展開
- 経路積分とシュレーディンガー方程式
- 虚数時間と統計力学
- 運動量空間でのファインマン核
第3章:WKB近似
- WKB近似
-- 多重積分の実行
-- 古典軌道の安定性と基準モード
-- ゼロ・モードと並進対称性
- ヴァン ヴレック行列式
- WKB近似
- 転回点での波動関数の接続と量子条件
- トンネル効果
第4章:調和振動子および関連する話題
- 量子論における調和振動子
- 振動する波束
- 経路積分による調和振動子の記述
-- 古典運動と作用積分
-- ファインマン核
- 第2量子化と場の量子論
-- 生成・消滅演算子
-- 第2量子化と場の演算子
-- フェルミ粒子
-- 場の量子論におけるグリーン関数
- コヒーレント状態経路積分
-- フェルミ系
第5章:エネルギー表示
- エネルギー表示のファインマン核と状態密度
- 停留位相近似
- 電子波のコヒーレンス:残像という見方
第6章:電子状態の時間発展と自己干渉による固有状態の形成
- 自由粒子
- 一定の外力下の電子
- 調和振動子
-- 離散準位の形成過程
-- 軌道反磁性とランダウ準位
-- シュタルク・ラダー準位
- ヘテロ結合
-- ポテンシャル障壁の透過
第7章:散乱問題における摂動論
- ポテンシャルによる粒子の散乱
- 摂動展開
- リップマン-シュウィンガー方程式
- ボルン近似
-- 諸量の関係
- 摂動問題における半古典近似
- 電子間相互作用
第8章:半古典近似でのダイナミクス
- 電子の軌道と動的WKB近似
- 動的WKB近似の計算例
-- 自由粒子
-- 壁での反射と量子井戸の準位
- トンネル効果とインスタントン
- 共鳴トンネル効果の時間解析
- 多次元空間での運動
付録A:解析力学のまとめ
- 一般化座標とラグランジアン
- 最小作用の原理
- 時間並進対称性とハミルトニアン
付録B:状態ベクトルを用いた表記
- 状態ベクトルを用いた関数の表現
- 変換理論と固有値問題
付録C:公式
参考文献
索引
























新年早々、変な質問で恐縮なのですが、上の記事の中で、「方程式の類似性からわかるように古典力学および量子力学における2つの状態は拡散していくことを意味している。自由粒子としての電子波(複素数波)も熱のように移動しながら拡散していくのだ」と仰られています。解説されている本を読んでいない状態での質問で申し訳ないのですが、シュレーディンガー方程式って拡散(熱)方程式にどのように性質が似ているんでしょうか。
私は物理学の素養が無いので数学としてしか語れませんが、次の3種類の方程式とその特解を見ますと、(∂2/∂2は2階の偏微分を意味します)
1.熱方程式 ∂u/∂t=∂2u/∂x2
2.シュレーディンガー方程式 i∂u/∂t=-∂2u/∂x2
3.波動方程式 ∂2u/∂t2=∂2u/∂x2
1.の特解 u(t,x)=exp(-t)sin(x)
2.の特解 u(t,x)=exp(i(x-t))=cos(x-t)+isin(x-t)
3.の特解 u(t,x)=cos(x-t)
となり、解の振る舞いからすると1.よりはやはり3.の仲間のように見えるのです(分散波と非分散波という違いはありますが)。1.の特解は指数関数的に定数(=0)に近づきますが、2.3.はそのような性質を持ちませんし。ファインマン経路積分の時間変数を複素変数に解析接続してウィーナー積分に持ち込んで考えると言う理論を見たことがありますから、全く無関連とは言えないのでしょうが、物理学に詳しいとねさんや常連の方々のご意見を聞きたいと思いコメントをアップしました。物理的に無意味な質問でしたらごめんなさい。
あけましておめでとうございます。僕は新年早々風邪をひいてしましました。(笑)今年も読んで楽しく、ためになる記事が書けるように頑張ります。
さて、ご質問いただいた内容ですが、今外出中でこの「量子波のダイナミクス」が手元にございませんので、ネット上から得られる情報を助けに解説させていただきます。
まず2.シュレーディンガー方程式と3.波動方程式ですが、微分方程式の左辺の階数が異なるため、この2つは違うタイプの方程式です。
また、2.シュレーディンガー方程式に対して例示されたu(t,x)=exp(i(x-t))は特解で、「時間に依存しないシュレディンガー方程式の定常解(平面波)」つまり定在波になっています。
今取り上げている現象を記述するためには、時間に依存しない定常解ではなく「時間に依存して変化していく波動関数の一般解」を求めなくてはいけません。一般解は特解(平面波)の重ね合わせで
ψ=Σcu
または
ψ(r,k)=∫c(k)u(k)exp(-iω(k)t)dk
で、このψもシュレディンガー方程式を満たします。
つまり2.シュレディンガー方程式の波動関数の一般解の時間発展(時間の経過によりどのように波動関数が変化していくか)を考えることによって拡散型の解が得られるということです。1.熱方程式との類似性は、時間に依存したシュレーディンガー方程式を虚数時間に拡張することによって得られます。
熱の伝導方程式の一般解とシュレディンガー方程式の時間発展をあらわした一般解は式を変形していくと共に「第一種フレドホルム積分方程式」の形でもあらすことができます。この式のK(x,t)の部分が積分核というもので、熱伝導では「熱核」、ファインマンの経路積分では「ファインマン核」と呼ばれているものです。「第一種フレドホルム積分方程式」については次のページでご確認ください。
積分方程式
http://ja.wikipedia.org/wiki/%E7%A9%8D%E5%88%86%E6%96%B9%E7%A8%8B%E5%BC%8F
また、次のようなページをお読みになると、波動関数が広がっていくことに納得いくと思いますがいかがでしょうか?
シュレディンガー方程式に従う粒子の時間発展:自由粒子
http://www.natural-science.or.jp/article/20100920222638.php
シュレディンガー方程式も、虚時間を導入することにより、拡散方程式に姿を変える。
http://www.astro.phys.s.chiba-u.ac.jp/~miyaji/class/keisan-buturi/2010/report-3.hint.html
時間に依存したシュレーディンガー方程式を虚数時間に拡張する。拡散方程式と同じ形になる。
http://www.solis.t.u-tokyo.ac.jp/introduction/B-7-02/B-7-0203.html
ネルソンの確率量子化法
http://www.aa.alpha-net.ne.jp/t2366/%E3%83%8D%E3%83%AB%E3%82%BD%E3%83%B3%E3%81%AE%E7%A2%BA%E7%8E%87%E9%87%8F%E5%AD%90%E5%8C%96htm.htm
特に次の動画は直観的にわかりやすいですね。
シュレディンガー方程式に従う粒子の時間発展
無限に深い2次元井戸型ポテンシャル2
http://www.natural-science.or.jp/article/20101013171121.php
無限に深い2次元井戸型ポテンシャル3
http://www.natural-science.or.jp/article/20101013204042.php
まず、この 森藤正人「量子波のダイナミクス」を取り上げたいと思っています。
ところで、アイシャム「量子論」という本があるのですが、
http://www.amazon.co.jp/gp/product/toc/4842703091/ref=dp_toc?ie=UTF8&n=465392
「量子論の理論形式」「量子論における概念的諸問題」「ベルの定理」
とか、僕には、面白かったです。
たいていの本では、正準交換関係は、天下りに与えられたり、
シューレデンガEQの結果から(つまり本末転倒)
ですが、
この本では、ウイグナーの定理とストーンの定理から導き出しています。
ブログ再開するお気持ちが固まったのですね。よかったです。
こちらの記事の引用、もちろん大歓迎です。
アイシャム「量子論」のアマゾンのページを見てみました。比較的新しい本なのですね。原書は1995年出版です。
Lectures on Quantum Theory: Mathematical and Structural Foundations
「量子力学の物理・数学・哲学の3つの側面が融合したバランスが図られ...」という感じがよさそうだなと思いました。
> この本では、ウイグナーの定理とストーンの定理から導き出しています。
読んでみたいです!
おっしゃられている拡散方程式の解は、
「両端の温度が0に固定されている場合の解」ρ=Asin(bx)exp(-ct) と思います。
で、
これと境界条件をあわせた、シュレーディンガー方程式は、
両端のψが0ということになるかと
思います。
この場合、シュレーディンガー方程式の解は、ψ=Asin(bx)exp(iwt)
となり、差異は、tに付くi の差だけです。
実軸上では、解の振る舞いは 全然違いますが、
複素平面上で、考えると「近い」と
言えなくもない と思いますが、
いかがでしょうか。
> kazuakiさんの疑問について、、、
> おっしゃられている拡散方程式の解は、
>「両端の温度が0に固定されている場合の解」ρ=Asin(bx)exp(-ct) と思います。
1.のことですね。これについては確かにそうですね。
でも、温度というか熱がゼロってどういう意味だろう。。。(自問自答中)
> この場合、シュレーディンガー方程式の解は、ψ=Asin(bx)exp(iwt)
> となり、差異は、tに付くi の差だけです。
> 実軸上では、解の振る舞いは 全然違いますが、
> 複素平面上で、考えると「近い」と
> 言えなくもない と思いますが、
いかがでしょうか。
2.についてはもちろん解は複素数ですが、3.の解は普通は実数だけではないでしょうか?(「普通は」というのは通常物理学でこの方程式を扱うときは、という意味です。)
もちろん、複素数での解も数学上ではありえますが、この場合2.と3.は確かに「近い」と言えなくもないですね。
0°C でなく、0°K のことです。
拡散の要因は、熱運動とするのが、普通なので、
0°K とすることで、閉じ込めと同じことになると思いますので。
引用文献は、
http://www.mech.kagoshima-u.ac.jp/~nakamura/math2/heat01.doc
の 2-4-2-1 です。
「近い」というより、似ていると言う方が適切でした。
sin と sinh が似ているという言い方と 同じ意味です。
温度0度とは絶対温度0度の意味だったわけですね。
> sin と sinh が似ているという言い方と同じ意味です。
そういう感じで「似ている」というのでしたら納得できました。
この2つの関数のグラフの画像見つけました。
http://userdisk.webry.biglobe.ne.jp/021/432/38/N000/000/000/129147253310316327309_sinh01.jpg