{〔第1章〕の復習(5)}@https://blog.goo.ne.jp/blogmura-yy/e/44f62cc03d4d7c0d33d6a4fe59e26331
/27094+[%55D1](緑: 確認中; 灰色: 確認済)
%50:実数で考える剰余類
`▼
(0)「実数で考える巡回群」の高校生向けの補足です
(1)「Wikipedia」以外の参考資料
[1_]「ガロア理論の頂を踏む」@https://www.beret.co.jp/books/detail/487
[2_]「このファイル」@https://blog.goo.ne.jp/blogmura-yy/e/44f62cc03d4d7c0d33d6a4fe59e26331
[3_]「物理のかぎしっぽ」@http://hooktail.sub.jp/sitemap.html
[4_]「ときわ台学」@http://www.f-denshi.com/000TokiwaJPN/01daisu/000daisu.html
[5_]「高校数学の美しい物語」@https://mathtrain.jp/elegant
[8_その他のWebサイト]/*「直接参照」*/
[81_]「ピークの定理(10)」@https://blog.goo.ne.jp/blogmura-yy/e/9a57ab5f6f42cf4d3c902d0229c0b4a0
[82_]「実数で考える巡回群」@https://blog.goo.ne.jp/blogmura-yy/e/1494b69f0bbb8c6d7793afb467dcafa0
[83_mathwords]「剰余類の意味と2つの姿」@https://mathwords.net/joyorui
[84_tanren]「日々是鍛錬」@https://www.hibikore-tanren.com/category/math/
[85_]「〔第1章〕の復習(5)」@https://blog.goo.ne.jp/blogmura-yy/e/44f62cc03d4d7c0d33d6a4fe59e26331
[86_]「〔第2章〕の復習(6)」@https://blog.goo.ne.jp/blogmura-yy/e/1494b69f0bbb8c6d7793afb467dcafa0
[87_]「〔第2章〕の復習(7)」@https://blog.goo.ne.jp/blogmura-yy/e/db7541e83f506a504199fa715a513b12
[88_]「〔第2章〕の復習(8)」@https://blog.goo.ne.jp/blogmura-yy/e/2cb7c35acfcc634cf14d095283143f6b
[9_]「Q&A」/*直接参照*/
[91_OK]「OKWave」@https://okwave.jp/
[92_goo]「教えて!goo」@https://oshiete.goo.ne.jp/
[93_Yahoo]「Yahoo知恵袋」@https://chiebukuro.yahoo.co.jp/
(2)「(1)」の参照例/
①[1_51P1]〔問1.1〕(pp.24-25)「ユークリッドの互除法」/*「ページの指定」*/
②[91_OK]「互除法」@https://okwave.jp/qa/q1771051.html
・[1_]のパラグラフの直接参照は「①」のように「%」を外して指定/*「リンクなし」*/
③[2_]は「%」を外してパラグラフIDのみを表示/*「リンクなし」*/
・[2_51D1]「記号の定義」
(3)目次
%51:剰余の表現/*「〔問1.1〕;〔問1.2〕;〔問1.8〕」*/
%52:2次方程式/*「複素数」*/
%53:数平面/*「三角関数」*/
%54:行列式/*「置換」*/
%55:剰余類/*「〔問1.4〕(pp.36-37)」*/
%56:巡回群/*「〔問1.5〕(pp.38-40)」*/
(4)記号の変更
`▲「(1), (3)」を修正
%51:剰余の表現
%51D1:記号の定義/*「剰余の表現」*/
`▼
(1)実数の集合を「`R」,整数の集合を「`Z」,自然数(正の整数)の集合を「`N」で表し次のように定義.
(2)「x」(x ∈ `R)に対して「x」を超えない最大の整数を「Γ(x)」で表し、「Δ(x)」を
「Δ(x) = x - Γ(x)」と定める.
(3)入門書と比較しやすいように「k ∈`N」である変数「k」の関数
「γ3(k) = (k mod 3)」,「γ5(k) = (k mod 5)」を考える./*「γ5(k) = 5 * Δ(k / 5) = k」*/
/*変域を明示していない変数(英小文字)は自然数とみなす*/
(4)参考資料
①[_変数の変域]@https://ja.m.wikipedia.org/wiki/変数_(数学)
②[_関数]@https://ja.wikipedia.org/wiki/関数_(数学)
③[5_ユークリッドの互除法の証明と不定方程式]@https://mathtrain.jp/euclid
(5)自然数「m」,「n」の「最大公約数」を「GCD(m, n)」,「最小公倍数」を「LCM(m, n)」で表す.
/*「m * n = GCD(m, n) * LCM(m, n)」*/
(6)除算「k / 5」の剰余「k - Γ(k / 5) = Δ(k / 5)」の値はつねに「γ5(k - 1)」で考える.
`▲
%51P1:〔問1.1〕(pp.24-25) /*「ユークリッドの互除法」*/
`▼
(0)「GCD(851, 185)」を求めよ
(1)「N = M * Q + R」(0 ≦ R < M)とすると「N = M * Γ(N / M) + M * R」
(2)「`GCD(N, M)=`GCD(M, (N mod M))」./*〔定理1.1〕*/
(3)互除法の計算「Δ(851 / 185) = Δ(111 / 185)」,「Δ(185 / 111) = Δ(74 / 111)」,
「Δ(111 / 74) = Δ(37 / 74)」「Δ(74 / 37) = Δ(0 / 37)」は一つの式で表現できる.
(4)慣用の「連分数★」の略記法では「851 / 185 = {4; 1, 1, 1, 2}」
★https://ja.wikipedia.org/wiki/連分数
(5)「(正規)連分数展開」の末尾は「Δ(1 / K)」./*「Δ(K / 1) = 0」*/
(6)「(4)」の右辺のような表現では元の「分数」が分からないので,「Frac`(851, 185;(111, 74, 37, 0))」
のように「剰余」の順列で表示すると末尾の「0」の直前の値が分母と分子の最大公約数になる.
・「Δ(74 / 37)」の剰余を「0」と考える./*「`R」上の計算 */
(7)「Δ(17 / 5) = Δ(2 / 5)」,「Δ(5 / 2) = Δ(1 / 2)」,「Δ(2 / 1) = Δ(0 / 1)」だから,
「Frac`(17,5;(2, 1, 0))」であり「GCD(17, 5) = 1」
(8)「(3)」の連分数展開は「Frac`(23 * 37, 5 * 37; (3 * 37, 2 * 37, 37, 0))」
(9)「GCD(851, 185) = 37」/*「GCD(17, 5) = 1」であることを『17 と 5 は互いに素である』という*/
`▲【[81_411T1]】の部分コピーに加筆
%51P2:〔問1.2〕(pp.27-30)./*「1次不定方程式の一般的解法」*/
`▼
(0)「17 * x + 5 * y = 1」の一つの解を求めよ.
(1)「17 = 5 * 3 + 2」だから「17 * x + 5 * y 」を「5 * (3 * x + y) + 2 * x」に書き換える.
(2)「z = 3 * x + y」とおくと「(0)」の式は「5 * z + 2 * x = 1」と等価.
(3)「5 = 2 * 2 + 1」だから「w = 2 * z + x」とおくと「(2)」の式は「2 * w + z = 1」と等価.
(4)「2 * w + z = 1」の一つの解は「(w, z) = (0, 1)」
(5)「w = 2 * z + x」,「(w, z) = (0, 1)」より「x = -2」
(6)「z = 3 * x + y」,「(z, x) = (1, -2)」より「y = 7」
(7)「17 * x + 5 * y = 0」の解は「(x,y)=(-5 * k),17 * k)」(k ∈`Z)
(8)一般解は「(x, y)=(-(2 + 5 * k), 7 + 17 * k)」(k ∈`Z)
(9)「z」,「w」の定義式の右辺の「y」,「x」の係数を「1」にすることが肝要.
`▲【[81_411P2]】のコピーに加筆
%51P3:〔問1.8〕(pp.59-60)./*「中国の剰余定理」*/
`▼
(0)「Δ(A / 3) = Δ(1 / 3)」,「Δ(A / 5) = Δ(2 / 5)」,「Δ(A / 7) = Δ(3 / 7)」として
「Δ(A /105)」を求めよ./*「105 = 3 * 5 * 7」*/
(1)「F`(X,Y,Z) = 3 * Δ(X / 3) + 5 * Δ(Y / 5) + 7 * Δ(Z / 7)」とする.
(2)「F`(70, 0, 0) = Δ(1 / 3)」,「F`(0, 21, 0) = Δ(1 / 5)」,「F`(0, 0, 15) = Δ(1 / 7)」
(3)「3 * Δ(x / 3) = a」,「5 * Δ(x / 5) = b」,「7 * Δ(x / 7) = c」となる「x」は
「x = 70 * a + 21 * b + 15 * c」./*「Δ(70 / 3) = Δ(1 / 3)」*/
(4)「Frac`(105, 35; (25, 10, 5, 2, 0))」.
(5)「F`(X, Y, Z) = 1」の解「(70, 0, 0)」,「(0, 21, 0)」,「(0, 0, 15)」に対応するベクトル
「(Δ(1 / 3), 0, 0)」「(0, Δ(1 / 5), 0)」「(Δ(1 / 7), 0, 0)」を「`R^{3}」に
埋め込んだベクトルを,スカラー倍を整数倍に限定した実ベクトル空間の直交基底に使える.
(6)「(3)」の「x」が一般解
`▲【[81_416P8]】のコピーに加筆
%51D2:記号の定義/*「2次方程式」*/
`▼
(0)「虚数単位★」を「i_」として,方程式「x^{3} - 1 = 0」の解を求めよ.
①「f(x) = (x - 1) * (x^{2} + x + 1)」だから「f(1) = 0」/*「因数定理」*/
②「x^{2} + x + 1 = 0」の解は「x = ±i_ * sin(π / 3)」
(1)参考資料
①[_因数定理]@https://ja.wikipedia.org/wiki/因数定理
②[5_因数定理]@https://mathtrain.jp/factortheorem
③[_二次方程式の解の公式]@https://ja.wikipedia.org/wiki/二次方程式の解の公式
④[3_2次方程式の解の公式]@http://hooktail.sub.jp/mathInPhys/kainokoshiki/
⑤[_既約多項式]@https://ja.wikipedia.org/wiki/既約多項式
⑥[_多項式環]@http://www.f-denshi.com/000TokiwaJPN/01daisu/240rng.html
⑦[5_複素指数関数とオイラーの公式]@https://mathtrain.jp/eulerformula
(2)「x^{2} + x + 1」は実係数の多項式の積に分解できないので「`R」では「既約多項式」
`▲「(3)」を削除
%52:行列式
%52D1:記号の定義/*「行列式」*/
`▼
(0)次の連立1次方程式の解「(x, y)」を求めよ.
①a * x + b * y = p
②c * x + d * y =q
(1)参考資料
①[5_連立1次方程式]@https://mathtrain.jp/renritsu
②[3_LU分解]@http://www.hooktail.org/computer/index.php?LU%CA%AC%B2%F2
③[5_行列式]@https://mathtrain.jp/determinant
④[5_置換]@https://mathtrain.jp/permutation
⑤[5_差積]@https://mathtrain.jp/saseki
⑥[5_転置行列]@https://mathtrain.jp/transpose
⑦[5_逆行列]@https://mathtrain.jp/inversematrix
(2)行列「A」の「(i, j)要素」を「A_^{(i, j)}」で表すと,「(0)」の方程式は
①「A_{(1, 1) = a」「A_{(1, 2) = b」「A_{(2, 1) = c」「A_{(2, 2) = d」
②「A(x, y)^T = (p, q)^T」/*「□^T」は「□」の「転置」*/
③「a * d - b * c」を「A」の「行列式」といい、「det(A)」と表記.
④「D=det(A)」が「0」でなければ逆行列「A^{- 1}」が存在し,
「A^{- 1}_{(1, 1) = a / D」, 「A^{- 1}_{(1, 2) = - b / D」
「A^{- 1}_{(2, 1) = - c / D」,「A^{- 1}_{(2, 2) = d / D」
(3)連立1次方程式の解き方より「(1)④」の「置換」を読んでください.
(4)
`▲作業中
%53:数平面
%53D1:記号の定義/*「三角関数」*/
`▼
(1)「_xy平面」上の点を「P = (x, y)」( x^{2} + y^{2} > 0 ),「P」から「x軸」に下した
垂線の足を「H = (x, 0)」,原点を「O = (0, 0)」,「△POH」の 点「O」の頂角を
「θとして」関数「sin(θ)」「cos(θ)」を次式で定める
①「sin(θ) = y / r」,「cos(θ)= x / r」( r =(x^{2} + y^{2})^{1/2} > 0 )
(2)「P」の座標は「(x, y) = (r * cos(θ), r * sin(θ))」/*これを「P」の「極座標表示」という*/
[5_極座標]@https://mathtrain.jp/kyokuzahyo
(3)「e^{i_ * θ} = (cos(θ) + i_ * sin(θ)」だから「P」と「r * e^{i_ * θ}」は1対1に対応
/*「i_」は虚数単位.【2_51D2】/*「定義行以外では着色しない」*/
`▲
%54:剰余類
%54P1:〔問1.4〕(pp.36-37)/*「有限体での演算」*/
`▼
(0)5行5列の行列「A」の要素「A_{(i, k)}」に次の値を設定して「A」を表示せよ
①「A_{(i, j)} = γ5(i - 1) + γ5(k - 1)」
②「A_{(i, j)} = γ5(i - 1) * γ5(k - 1)」
(1)「①」の解/*緑:「i-1」茶:「k-1」*/
「 0 1 2 3 4
0 (0, 1, 2, 3, 4),
1 (1, 2, 3, 4, 0),
A = 2 (2, 3, 4, 0, 1),
3 (3, 4, 0, 1, 2),
4 (4, 0, 1, 2, 3)」
(2)「②」の解
「 0 1 2 3 4
0 (0, 0, 0, 0, 0),
1 (0, 1, 2, 3, 4),
A = 2 (0, 2, 4, 1, 3),
3 (0, 3, 1, 4, 2),
4 (0, 4, 3, 2, 1)」
(3)素数「m」を法とする剰余は実数体上の加法,乗法に関して「有限体」になる.
①[3_体]@http://hooktail.sub.jp/algebra/FieldBasic/
②[3_体]@http://hooktail.sub.jp/algebra/FieldDef/
③[5_]「有限体(ガロア体)」@https://mathtrain.jp/galoisfield
(3)【[2_151D](3)】の関数「γ5(k)」で考え,集合「`γ5」を次式で定める
「`γ5={γ5(k); (k∈`N)∧(k<6)}」/*「γ5(k) = 5 * Δ(k / 5) = k」*/
①「γ5(k)=(k mod 5)」だから「γ5(5) = 0」
②「γ5(- 2)」等は考えにくいので「k ∈ `N」とする
③「`γ5 = {1, 2, 3, 4, 0}」
`▲「(1)-(2)」のフォントは「Terminal」
%54D1:記号の定義/*「剰余類」*/
`▼
(1)「`Δ(k / M) = {Δ(k / M); k ∈ `Z}」(「k」は変数,「M」は定数 )を「M」を法とする剰余類
という./*集合には「`□」のように「`」を付加*/
(2)参考資料
①[3_剰余類]@http://hooktail.sub.jp/algebra/Remainder/
②[82_剰余類]@https://mathwords.net/joyorui
(3)【[2_151D](3)】の関数「γ5(k)」で考え,剰余類「`γ5」を次式で考える.
「`γ5={γ5(k); (k∈`N)∧(k<6)}」/*「γ5(k) = 5 * Δ(k / 5) = k」*/
①「γ5(k)=(k mod 5)」だから「γ5(5) = 0」/*「巡回群の考察時に重宝」*/
②「γ5(- 2)=((- 2) mod 5)」等は考えにくいので「k ∈ `N」とする
③「`γ5 = {1, 2, 3, 4, 0}」
(4)【[2_54P1](0)】の「γ5(i - 1) + γ5(k - 1)」「γ5(i - 1) * γ5(k - 1)」の値は
通常の加法と乗法の演算結果を「5」を法とする剰余で表示
①「(1)」の「0」になる要素から加法の逆元が分かる/*「1 + 4」,「2 + 3」*/
②「(2)」の「1」になる要素から加法の逆元が分かる/*「1 * 4」,「2 * 3」,「4 * 4」*/
(5)【[2_54P1](1)-(2)】と同様に6行6列の行列「A」の要素「A_{(i, k)}」に
「γ6(i - 1) + γ6(k - 1)」,「γ6(i - 1) * γ6(k - 1)」の値を設定して「A」を表示すると
①「γ6(i - 1) + γ6(k - 1)」の値は/*緑:「i-1」茶:「k-1」*/
「 0 1 2 3 4 5
0 (0, 1, 2, 3, 4, 5),
1 (0, 1, 2, 3, 4, 0),
A = 2 (2, 3, 4, 0, 1, 2),
3 (3, 4, 0, 1, 2, 3),
4 (4, 5, 0, 1, 2, 3),
5 (5, 0, 1, 2, 3, 4)」
②「γ6(i - 1) * γ6(k - 1)」の値は/*緑:「i-1」茶:「k-1」*/
「 0 1 2 3 4 5
0 (0, 0, 0, 0, 0, 0),
1 (0, 1, 2, 3, 4, 5),
A = 2 (0, 2, 4, 0, 2, 4),
3 (0, 3, 0, 3, 0, 3),
4 (0, 4, 2, 0, 4, 2),
5 (0, 5, 4, 3, 2, 1)」
(6)【[2_54D1](1)】の「`γ5」を「5」を法とする剰余類という.同様に「6」を法とする剰余類は
「`γ6 = {γ6(k); (k ∈ `N) ∧ (k < 6)}」.
/*「γ3(2) = γ5(2) = 2」であるが「γ3(2) ∈ `γ3」,「γ5(2) ∈ `γ5」*/
(7)「`Δ(k / 3)」,「`Δ(k / 5)」の元であれば「Δ(2 / 3) ≠ Δ(2 / 5)」
`▲「(1)-(3)」を更新「(6)」を追加
%55:巡回群
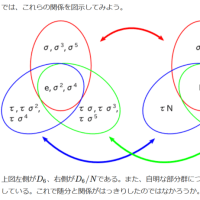
%55P1:〔問1.5〕(pp.38-40)/*「正六角形の回転」*/
`▼
(0)「_xy平面」上の点「P = (1, 0)」を原点「(0, 0)」の周りを左回りに
「2 * π / 6」回転する操作を「σ」として次の問に答えよ/*「表現を変えています」*/
①点「σP」の座標を示せ
②「σ(σP)」の座標を示せ
③「σ((σ^{k})P)=(σ^{k + 1})P」として「σ^{k})P = P」となる「k」の値を示せ.
④「σ^{i})P =σ^{k})P」ならば「σ^{i} = σ^{k}」と考えて
「σ^{i}・σ^{k}」の演算表を示せ
(1)参考資料
[3_有限巡回群]@http://hooktail.sub.jp/algebra/FiniteCyclicGroup/
[4_巡回群]@http://www.f-denshi.com/000TokiwaJPN/01daisu/020gun.html
(2)「(0)」の解は
①(cos(π / 3), sin(π / 3))
②(cos(2 * π / 3), sin(2 * π / 3))
③「Δ(k / 6) = 0」となる「k」
④[1_1P5]の表(p.40)参照/*「σ^{6} = e」*/
(3)「σΔ(k / 6) = Δ((k + 1) / 6)」と考えると「{σΔ(k / 6); k∈ `N}」は有限巡回群
(4)「群」には元が通常の式のものと,元が置換や回転のような操作のものがある
`▲続きは「〔第2章〕の復習(6)」を見てください
%55D1:記号の定義/*「巡回群」*/
`▼
(1)「σ(γ5(k)) = γ5(k + 1)」と定める.
(2)「`γ5 = {1, 2, 3, 4, 0}」であるから「σ(`γ5) = {σ(x); x ∈ `γ5}」と定めると
「σ(`γ5) = {2, 3, 4, 0, 1}」
`▲追加@K31
%56:「〔第2章〕の復習(6)」との対応表(灰色: 不在)
`▼
%51:剰余の表現
%51P1:〔問1.1〕(pp.24-25) /*「ユークリッドの互除法」*/
%51P2:〔問1.2〕(pp.27-30)./*「1次不定方程式の一般的解法」*/
%51P3:〔問1.8〕(pp.59-60)./*「中国の剰余定理」*/
%51D1:記号の定義/*「1次不定方程式」*/ ⇒/*【[82_61D1]】*/
%52:2次方程式
%52D1:記号の定義/*「複素数」*/ ⇒/*【[82_63D2](1)】*/
%53:数平面
%53P1:〔問3.0〕/*「極座標」*/
%53D1:記号の定義/*「三角関数」*/⇒/*【[82_64D1]】*/
%54:剰余類
%54P1:〔問1.4〕(pp.36-37)/*「有限体での演算」*/ ⇒/*【[82_62D1](5)】*/
%54D1:記号の定義
%55:巡回群
%55P1:〔問1.5〕(pp.38-40)/*「正六角形の回転」*/ ⇒/*【[82_63D1](1)】*/
`▲[82_]@https://blog.goo.ne.jp/blogmura-yy/e/1494b69f0bbb8c6d7793afb467dcafa0
aa














※コメント投稿者のブログIDはブログ作成者のみに通知されます