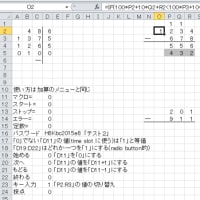
{ピークの定理(11)}@https://blog.goo.ne.jp/blogmura-yy/e/f3903724cb9252cbd5901f3ffce5fbea
作業中/8366(確認のために公開)(茶: 確認中; 灰色: 確認済; 緑: 非慣用記法)
%0:ピークの定理(11)/*「〔第1章〕の紹介」*/
「異端爺」の無責任メモ.無理数【π】を用いて分数を使わない「正統派」の説明
【整数論の入門書】に反抗./*【[%81A](6)】*/
%4:〔第1章〕の「問(P)」・「定義(D)」・「定理(T)」の一覧
`▼
〔§1.1〕/*ユークリッドの互除法*/P1(24),T1,P2(27),T2,T3
〔§1.2〕/*剰余類 */P3(33),D1,D2,T1,4,P4(37)
〔§1.3〕/*巡回群 */P5(38),D3
〔§1.4〕/*群の同型 */D4
〔§1.5〕/*部分群 */P6(50),T5
〔§1.6〕/*群の直積 */D5,P7(55),T6,P8(59),T7,T8
〔§1.7〕/*既約剰余類群 */P9(66),D6
〔§1.8〕/*(Z/pZ)^{*}の構造分析*/P10(69),T10
〔§1.9〕/*原始根で生成 */P11(74),T11,P12(77),T12,T13,T14
〔§1.A〕/*原始根の存在証明 */T15,T16,P13(84),T17
〔§1.B〕/*(Z/pZ)^{*} の構造 */TI8,L18,T19,L19,T20
`▲〔問〕以外は目次で対応するページが分かる.
%41:〔第1章〕のパラグラフの紹介
%41T1:〔定理1.1〕/*互除法の原理*/
`▼
(1)「N = M * Q + R」(0 ≦ R < M)とすると「N = M * Γ(N / M) + M * R」
(2)「`GCD(N, M)=`GCD(M, (N mod M))」./*〔定理1.1〕*/
(3)互除法の計算「Δ(851 / 185) = Δ(111 / 185)」,「Δ(185 / 111) = Δ(74 / 111)」,
「Δ(111 / 74) = Δ(37 / 74)」「Δ(74 / 37) = Δ(0 / 37)」は一つの式で表現できる.
(4)慣用の「連分数」の略記法では「851 / 185 = {4; 1, 1, 1, 2}」
(5)「(正規)連分数展開」の末尾は「Δ(1 / K)」./*「Δ(K / 1) = 0」*/
(6)「(4)」の右辺のような表現では元の「分数」が分からないので,「Frac`(851, 185;(111, 74, 37, 0))」
のように「剰余」の順列で表示すると末尾の「0」の直前の値が分母と分子の最大公約数になる.
・「Δ(74 / 37)」の剰余を「0」と考える./*「`R」上の計算 */
(7)「Δ(17 / 5) = Δ(2 / 5)」,「Δ(5 / 2) = Δ(1 / 2)」,「Δ(2 / 1) = Δ(0 / 1)」だから,
「Frac`(17,5;(2, 1, 0))」であり「`GCD(17, 5) = 1」
(8)「(3)」の連分数展開は「Frac`(23 * 37, 5 * 37; (3 * 37, 2 * 37, 37, 0))」
(9)命題と集合の表現に「集合と写像[1]★」の記号を使う./*空集合は「{}」*/
★[1]http://blog.goo.ne.jp/bonsai-chat/e/f86b17168cffd2e093025838d9df34a1
`▲
%41P2:〔問1.2〕
`▼
(0)「17 * X + 5 * Y = 1」の一つの解を求めよ.
(1)「17 = 5 * 3 + 2」だから「17 * X + 5 * Y 」を「5 * (3 * X + Y) + 2 * X」に書き換える.
(2)「Z = 3 * X + Y」とおくと「(0)」の式は「5 * Z + 2 * X = 1」と等価.
(3)「5 = 2 * 2 + 1」だから「W = 2 * Z + X」とおくと「(2)」の式は「2 * W + Z = 1」と等価.
(4)「2 * W + Z = 1」の一つの解は「(W, Z) = (0, 1)」
(5)「W = 2 * Z + X」,「(W, Z) = (0, 1)」より「X = -2」
(6)「Z = 3 * X + Y」,「(Z, X) = (1, -2)」より「Y = 7」
(7)「17 * X + 5 * Y = 0」の解は「(X,Y)=(-5 * K),17 * K)」(K'∈`Z)
(8)一般解は「(X,Y)=(-(2 + 5 * K), 7 + 17 * K)」(K'∈`Z)
(9)「Z」,「W」の定義式の右辺の「Y」,「X」の係数を「1」にすることが肝要.
`▲原著の卓越した「1次不定方程式」解法の要約
%41P4S1:〔問1.4〕の復習
`▼
(0)「5」で割ると「K'」余る整数の集合(「5」を法とする「剰余類」)を「`Δ(K' / 5)'」(5 ∈ `N)で表わす.
(1)「Δ(3 / 5)」は変数「K'」の値が「3」のときの式,「5」は前提条件「5 ∈ `N」を満たす定数.
(2)「`Δ(K1 / 5)' + `Δ(K2 / 5))'」「`Δ(K1 / 5)' * `Δ(K2 / 5)'」の演算表を作れ.
/*「`Δ(0 / 5)'」を「`Δ(5 / 5)'」で代替*/
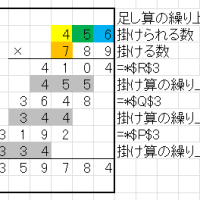
(3)「K1 = 5 * K1Q + K1R」(K1R < 5)「K2 = 5 * K2Q + K2R」(K2R < 5)とおくと
「K1 + K2 = 5 * (K1Q + K2Q) + (K1R + K2R)」
「K1 * K2 = 25 * (K1Q * K2Q) + 5 * (K1Q + K2Q) + (K1R * K2R)」
(4)「Δ((K1 + K2) / 5)=Δ((K1R + K2R) / 5)」
(5)「Δ((K1 * K2) / 5)=Δ((K1R * K2R) / 5)」
(6)答えは〔p.37〕の表.
`▲【[%412P4].[%17]】のコピーに加筆
%41P8:〔問1.8〕
`▼
(0)「Δ(A / 3) = Δ(1 / 3)」,「Δ(A / 5) = Δ(2 / 5)」,「Δ(A / 7) = Δ(3 / 7)」として
「Δ(A /105)」を求めよ./*「105 = 3 * 5 * 7」*/
(1)「F`(X,Y,Z) = 3 * Δ(X / 3) + 5 * Δ(Y / 5) + 7 * Δ(Z / 7)」とする.
(2)「F`(70, 0, 0) = Δ(1 / 3)」,「F`(0, 21, 0) = Δ(1 / 5)」,「F`(0, 0, 15) = Δ(1 / 7)」
(3)「3 * Δ(X / 3) = A」,「5 * Δ(X / 5) = B」,「7 * Δ(X / 7) = C」となる「X」は
「X = 70 * A + 21 * B + 15 * C」./*「Δ(70 / 3) = Δ(1 / 3)」*/
(4)「Frac`(105, 35; (25, 10, 5, 2, 0))」.
(5)「F`(X, Y, Z) = 1」の解「(70, 0, 0)」,「(0, 21, 0)」,「(0, 0, 15)」に対応するベクトル
「(Δ(1 / 3), 0, 0)」「(0, Δ(1 / 5), 0)」「(Δ(1 / 7), 0, 0)」を「`R^{3}」に
埋め込んだベクトルを,スカラー倍を整数倍に限定した実ベクトル空間の直交基底に使える.
`▲「中国の剰余定理」/*【[%416P8].[%17]】のコピーに加筆*/
%41D6S1:〔定義1.6〕の復習
`▼
(0)「`Z/(□)`Z」の部分集合「{K; ((K * □) ∈ `N) ∧ K < M)∧ (GCD(K, M) = 1)}」を
「`Δ(K'/ M)"」と略記して, これを既約剰余類群と称する.
(1)〔p.65〕の「`Δ(K'/ 6)'」の演算表は次式で計算.
「`Δ(K1'/ 6)' + `Δ(K2'/ 6)' = `Δ((K1'+ K2') / 6)'」
「`Δ(K1'/ 6)' * `Δ(K2'/ 6)' = `Δ((K1'* K2') / 6)'」
(2)〔p.66〕の「`Δ(K'/ 10)"」の演算表は「`Δ(K'/ 10)'」の演算表から.
「(GCD(K', M) = 1」である元【K' ∈ {1,3,7,9}】を選んで作成.
(3)「(1)」の足し算で「Δ(K' / M)」の逆元は「Δ((- K') / M)」.
/*「W`(0 / M) = 1」になるので「Δ(M / M)」と「Δ(0 / M)」を使い分け?*/
(4)「`Δ(K' / 6)'」の元を自然数で表現したければ「Δ(6 / 6)」を使う.
/*「互除法」の漸化式も「Δ(K / 1) = 0」で終了.「Δ」は重宝:【[%51BM2](6).[%19★]】*/
★https://blog.goo.ne.jp/blogmura-yy/e/04277093ed558c6cf749796d601a161f
`▲
%41P6M1:〔問1.6〕(50)の復習
`▼
(0) 剰余類「`Δ(K' / 6)'={Δ(K / 6); (K ∈ `Z)∧(K'< 7)}」(K' ∈ `Z)の元の一部を用いて群を作れ.
(1)一般に「`Δ(K1' / M)'」,「`Δ(K2' / M)'」に対して次式が成立.
「Δ(K1' / M)' + Δ(K2' / M)' = Δ((K1' + K2') / M)'」/*「`R」上の加算*/
「Δ(K1' / M)' * Δ(K2' / M)' = Δ((K1' * K2') / M)'」/*「`R」上の乗算*/
(2)【[%413D3]】の「・」を「`Δ(K1' / 6)'・`Δ(K2' / 6)' = `Δ(K1' / 6)' * `Δ(K2' / 6)'」
と定めると「`Δ(K1' / 6)'・`Δ(K2' / 6)' = `Δ((K1'+ K2') / 6)'」.【集合に対する演算】.
(3)「∠(K' / M) = Δ((2 * π) / (K'/M)」,
「W`(K' / M) = cos(∠(K' / M))+_i * sin(∠(K' / M))」
と定めると 実数「Δ(K' / 6)」(K'∈ `Z)と複素数「W`(K' / 6)」は1対1に対応する.
(4)「`Δ(K' / 6)'」の部分集合が群になるためには「Δ(6 / K') = 0」であることが必要./*要逆元*/
(5)「(0)」の問の解答は 「{`Δ(K' / 1)',`Δ(K' / 2)',`Δ(K' / 3)' `Δ(6' / 6)' }」.
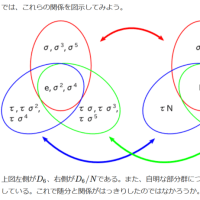
「正統派」は整数化するから式が分かり難くなる./*対応する群は「{e, <σ^{3}>, <σ^{2}>, C_{6}}」*/
〔問1.13〕の解法〔pp.84-85〕から予想できるように原始根の探索は簡単ではなさそう.
/*「Δ((200 * 300) / 41)」は高校生でも計算できる*/
(6)「σ^{K}」で考えている演算【・】は「*」だけ.「+」は簡単だから無視?.
`▲/*【[%415P6].[%19]】のコピーに加筆*/
%41Z:あとがき
`▼
(0)原著では〔第1章〕で複素数を使っていませんが,高校生も使い慣れている複素数を
を使いました:記号「Δ」は一般には通用しないので試験の解答やレポートに使わないでください.
(1)〔定理1.16〕の説明は分かり難そうなので「`Δ(K'/41)'」の原始根を
「 cos(360°/41) + _i * sin(360°/41)」のように表現しました.
(2)一般に「_xy平面上」上の点を「W`(K' / M) = exp(_i*∠`(K' / M))」
で考えると〔定理1.19〕の同型写像「φ」が分かりやすくなります.
`▲
%5:補遺/*[%81A](4)*/
`▼
%51P6M1:【`[%113]】/*「1P6」:〔問1.6〕*/
%51P6M2:【`[%113]】
%51P6M3:【`[%113]】
%51D3S1:【`[%114]】/*「1D3」:〔定義1.3〕*/
%51TK:【`[%114]】/*「1TK」:〔定理1.20〕*/
%51TKM1:【`[%114]】
%51TKM2:【`[%114]】
`▲`{「ピークの定理」への補足 `}@https://blog.goo.ne.jp/blogmura-yy/e/291675702b4ba0355242fbd4efad28b5
%8:変更履歴
%81A:[%1A]での変更
`▼
(0)[%819]までの変更を踏襲
(1)各パラグラフ(「P」,「D」,「T」)には 無責任メモに「%□M」を,単なる補遺には「%□S」を付加する.
(2)旧記法「`Z / (a)`Z」は紛らわしいので[%1A]以降では「`Z / ((a)`Z)」と表記. /*「a ∈ `R」*/
(3)本文に冗長なコメント【□】を適宜挿入/*「□」を薄茶色にするのはオプション*/
(4)「[%5:□]」を「[%5:□M□]」に変更./*「らくがき」→「補遺」*/
(5)[%5].[%1A]で参照したい`{「ピークの定理」への補足`}の記事のパラグラフID[%6□]を[%5□]に変更.
(6)「itangy={bonsai-chat, blogmura-yy, ep58-kit}」とし,「itangy」の「gooID」で投稿したブログ」を
「itangy」(異端爺)のブログと総称.
(7)`{「ピークの定理(11)」`}を作成.
`▲
aa