〔第２章〕の復習（８）

{〔第２章〕の復習（８）}@https://blog.goo.ne.jp/blogmura-yy/e/2cb7c35acfcc634cf14d095283143f6b/
/10267+[%74P1]（茶: 確認中; 灰色: 確認済; 緑: 非慣用記法）

---

%80:複素数で考える商群
「〔第2章〕の復習（７）」が「25000字」を超えたので[%64]以降をこのファイルに移動．

%801:参考資料`▼/*【「[1_601]】と同じ.*/`▲
%802:記事の参照`▼/*【「[1_602]】と同じ.*/`▲
%803:目次【の復習】
`▼

---

　%70:複素数で考える商群
　%71:多項式環/*「実数体の拡大」*/
　%72:正規部分群/*「g・`H = H・g^{- 1}」*/
　%73:商群/*「`Δ(K'/M)'」*/
　%74:可解群

---

`▲

%804:各パラグラフの問・定義・定理【の追加】
`▼

---

%71D1:記号の定義/*「多項式環」*/
%72D1:記号の定義/*「正規部分群」*/
%73D1:記号の定義/*「商群」*/
%74P1:〔問4.1〕/*「可解群」*/

---

`▲

%71:多項式環

%71D1:記号の定義/*「多項式環」*/
`▼

---

(0)実数体を複素数体に拡大する解説を調べて要点を示せ．
(1)参考資料
　①[_多項式環#体上の一変数多項式環_K[X]]@https://ja.wikipedia.org/wiki/多項式環#体上の一変数多項式環_K[X]
　②[3_拡大体]@http://hooktail.sub.jp/algebra/ExtensionField/
　③[4_]「８　体の拡大とn次代数方程式の解法へ」@http://www.f-denshi.com/000TokiwaJPN/01daisu/280rng.html
　④[_単拡大]@https://ja.wikipedia.org/wiki/単拡大
(2)「(1)①」からの引用
実例として、複素数体「 `C」は実数体「`R」に「 i_^{2} + 1 = 0」を満たす i_ を唯一つ付け加えて得られる。
それに応じ、多項式「X^{2} + 1」は「`R」上既約であって 
C ? R [ X ] / ( X ^{2} + 1 ) /*「\textstyle \mathbb {C} \simeq \mathbb {R} [X]/(X^{2}+1)」*/ 
という同型が成立する。/*「 ? 」の記号は「画像フォルダ★」に保存*/
　★https://blogimg.goo.ne.jp/user_image/4d/91/6893a2d16b6b470123c299910be9c50c.png
(3)「(1)②」からの引用
ここで，拡大体の表記法を紹介しておきます．体「Ｆ」に新たに代数的な元
「θ」を添加して拡大体を作るとき，その拡大体を「Ｆ(θ)」のように書きます．
特に，元を一個だけ添加して得られる拡大体を「単純拡大体」と呼びます．/*「`R(i_)」*/
複素数体は，実数体の拡大体で，拡大次数は「2」であることを確認してみてください．

---

`▲「i_」は虚数単位/*【[].[]】*/

%72:正規部分群

%72D1:記号の定義/*「正規部分群」*/
`▼

---

(0)「Δ(K'/ M)"」は正規部分群であることを示せ
(1)参考資料
　①[_正規部分群]@https://ja.wikipedia.org/wiki/正規部分群
　②[7_正規部分群]@https://www.sist.ac.jp/~kanakubo/research/hosoku/seiki_bubun.html
　③[3_正規部分群に関する幾つかの性質]@http://hooktail.sub.jp/algebra/NormalSubgroup2/
　④[3_同型定理]@http://hooktail.sub.jp/algebra/Isomorphism/
　⑤[4_正規部分群]@http://www.f-denshi.com/000TokiwaJPN/01daisu/080gun.html
　⑥[_同型定理]@https://ja.wikipedia.org/wiki/同型定理
(2)【[%423TF](1).[%1B]】の紹介（灰色）
　@https://blog.goo.ne.jp/blogmura-yy/e/45a9e6897d614ae2de6acbb1e9dd5736
------------------------------------------------------------
(0)「H」,「N」が「G」の部分群であるとき
　(ア)「H∩N」は「G」の部分群
　(イ)特に「N」が「G」の正規部分群であれば「HN」は「G」の部分群
(1)原著の「HN」〔p.145〕は分かり難いので，「(`H1)(`N2)」を
　「`H1(`N2) = {(h, n); (h ∈ `H1) ∧ (n ∈ `N2)}」と表示．
(2)上のように定めた「f: G → (G / N)」を「自然準同型」と呼びます．/*〔p.147〕*/
------------------------------------------------------------
(3)【[1_61D1](3)】で定義した「`G=Δ(K'/M)'」( K'∈ `N(M) )に対して次の記号を定義．
　①「`G」の元「x'」,「y'」の和を「`R」の加法で計算することを「GR`(「＋」; `G)」と表記．
　②「`G」の元「x'」,「y'」の積を「`R」の乗法で計算することを「GR`(「＊」; `G)」と表記．
　③「`G」の部分集合「H」,「N」に対して「`H(`N)」を次式で定義．
　　「`H(`N) = {(h, n); (h ∈ `H) ∧ (n ∈ `N)}」/*「非慣用記法」*/
(4)【[%62D1](7)】:
------------------------------------------------------------
　②「GF`(「＊」; `Δ(K' / M)')」/*「Ｍ」は素数;「Δ(M / M)」と「Δ(0 / M)」を使い分ける*/
　　　/*半角英数にすると「*」（上付き: Arial）になる*/
　③「`Δ(K' / M)*」はスマホでは「`Δ(K' / M)*」になるので「`Δ(K' / M)"」を使用
------------------------------------------------------------
(5)

---

`▲背景色が無視される

%73:商群

%73D1:記号の定義/*「商群」*/
`▼

---

(0)「`G=`Δ(K'/ 3)'」の元を示せ．
(1)参考資料
　①[_商群]@https://ja.wikipedia.org/wiki/商群
　②[3_商群]@http://hooktail.sub.jp/algebra/QuotientGroup/
　③[81_noppoman]「商群」@https://note.com/noppoman/n/nb4bd7142700b
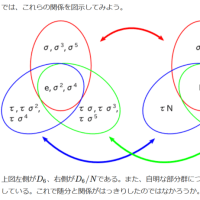
(2)「`Δ(K'/ M)'={Δ(K/ M); K ∈ `N(M)}」/*【[1_61D1](3)】*/だから
　 「(0)」の解は「`G = {`Δ(1/ 3)', `Δ(2/ 3)', `Δ(3/ 3)'}」
(3)「`Δ(K'/ 3)'」は「Δ(K'/ 3)」を「代表元」とする「M」を法とする剰余類の
　 元(集合)であり，慣用記法の「`Z/ 3 `Z」に等しい
(4)このブログの記法では「`Z/ 3 `Z」は「`Δ(K'/ 3)」( K ∈ `Z )と同じ集合
(5)「(1)⑤」の具体例の「あらすじ」
------------------------------------------------------------
①noteではtexがサポートされていないので、オーバーラインが表記できません。
そのため、以後はもうひとつの書き方である[x]で剰余類を表記します。
Z/3Z = { [0], [1], [2] }
②上で示した合同関係とその演算を持ち込めるか考えていきましょう。
③Gを群、Hをその部分群とするとき、 g＊H = H = H＊g
④Hが正規部分群であれば、Hの元の違いを同一視あるいは無視することで、
Gの元を同一視できるということを言っています。
⑤この正規部分群HでGを割ったG/Hを商群といいます。
⑥f: G -> G/Hが準同型写像である時、
π: G -> G/ker(f)となるπを自然な写像と定義しました。
つまり、G/Ker(f)は商群だったのです。
⑦3Z = [0]なので、φをZからZ/3Zへの準同型写像とすると、
ker(φ) = {x ∈ Z | φ(x) ∈ [0]} = 3Z
ここまで理解が進んだらもう準同型定理の「可換図式」がクリアに見えますよ。
------------------------------------------------------------
(6)

---

`▲

%74:可解群

%74P1:〔問4.1〕/*「可解群」*/
`▼

---

(0)「`Δ(K / M)"」は可解群であることを示せ．
(1)参考資料
　①[_群_(数学)]@https://ja.wikipedia.org/wiki/群_(数学)#可解群・交換子群・冪零群
　　・[_可解群]@https://ja.wikipedia.org/wiki/可解群
　②[3_ガロア群と可解群]@http://hooktail.sub.jp/algebra/Radicals/
　③[3_]「可解群について補足」@http://hooktail.sub.jp/algebra/SolvableGroupsApp/
　④[4_]「10-2　 交換子群と可解群」@http://www.f-denshi.com/000TokiwaJPN/01daisu/101gun.html
　⑤[6_peng225]「群が可解でないための条件」@http://peng225.hatenablog.com/entry/2017/09/22/143833
　⑥[7_]「可解群」@https://www.sist.ac.jp/~kanakubo/research/hosoku/kakaigun.html
(2)「(1)⑥」の紹介/*「過剰引用を自粛」*/
------------------------------------------------------------
対称群が、開法で正規部分群に縮小し、さらにその中の正規部分群に縮小し、
最終的に正規部分群でもある恒等置換一つになる必要があるという事だ。
この事を記号で書くと、以下のようになる。
このような列を正規列という。
ガロアは、式の値を不変にする解の置換の群が以下の条件を満たすとき、
方程式が代数的に解ける必要十分条件である事を見出した。
①正規列を持つ（最後は恒等置換となる）。
②正規列の全ての剰余群（上記の例ではSn/H0、H0/H1等）が、巡回群となる。
この条件を満たす群を、方程式が解けるという意味で可解群という。
------------------------------------------------------------
(3)(4)

---

`▲

aa