{〔第5章〕の紹介(1)}@https://blog.goo.ne.jp/blogmura-yy/e/6dc9f9cbb040fe386aafe5307ec1d7c8
/26177+[%45TZ2](茶: 確認中; 灰色: 確認済; 緑: 非慣用記法)
%0:〔第5章〕の紹介(1)
%1:参考資料`▼【〔第2章〕の復習(9)】`▲
%2:資料の参照
`▼
(0)参照の基本形は『「`RefNo[`Site_`ID]」「`Title」@`URL」』
(1)参考資料
①[1_]「〔第2章〕の復習(8)」@https://blog.goo.ne.jp/blogmura-yy/e/2cb7c35acfcc634cf14d095283143f6b/
②[2_]「このファイル」@https://blog.goo.ne.jp/blogmura-yy/e/6dc9f9cbb040fe386aafe5307ec1d7c8
③[78_]「ピークの定理への補足」@https://blog.goo.ne.jp/blogmura-yy/e/291675702b4ba0355242fbd4efad28b5
④[79_]「ピークの定理(□)関連資料」@https://blog.goo.ne.jp/blogmura-yy/e/e8b60af195f9178367fb30154bde7914
⑤[_ガロア理論]@https://ja.wikipedia.org/wiki/ガロア理論
⑥[_ガロア理論の基本定理]@https://ja.wikipedia.org/wiki/ガロア理論の基本定理
(2)「③」,「④」は「①」と同じ
(3)「①」を参照しながら「②をオンラインで直接編集」./*「③を使わない」*/
(4)このファイルでは命題「∃f, Imorph`(f; f(S1), S2)」を「S1 `=~ S2」(ゴシック)と略記.
/*【[%414D4](4).[%17]】*/
(5)「~」(ゴシック)を逆写像「f^{-1}(x)」の略記「f~(x)」にも使う./*「使用パラグラフで注記」*/
`▲「~」はスマホでは中央に表示される./*「フォント無指定の半角文字はArial?」*/
%3:記事の修正`▼【[2_2](3)】`▲/*「[2_2]=[%2].「このファイル」」*/
%4:抄録
%451:〔§5.1〕(271)/*Q(3^{1 / 2})の対称性*/での追加
`▼
%45P1:〔問5.1〕(272)
%45D1:〔定義5.1〕(273)/*体の定義*/
%45D2:〔定義5.2〕(280)/*体の同型写像*/
%45T1:〔定理5.1〕(282)/*有理数は同型写像で不変*/
`▲
%45P1:〔問5.1〕(272)
`▼
(0)「a = 5 + 2 * 3^{1 / 2}」「b = 7 + 4 * 3^{1 / 2}」として次式の値を求めよ.
①「a + b」②「a - b」③「a * b」④「a / b」
(1)参考資料
①〔定義5.1〕(273)
②[_体]@https://ja.wikipedia.org/wiki/体_(数学)
③[_有理数体]@https://ja.wikipedia.org/wiki/有理数
④[_拡大体]@https://ja.wikipedia.org/wiki/体の拡大
⑤[3_拡大体]@http://hooktail.sub.jp/algebra/ExtensionField/
(2)「(0)」の解は「Q(3^{1 / 2})」の元で
①「12 + 6 * 3^{1 / 2}」
②「- 2 - 2 * 3^{1 / 2}」
③「59 + 34 * 3^{1 / 2}」
④「5 + 2 * 3^{1 / 2}」
(3)「Q(3^{1 / 2})」は有理数体に方程式「x^{2}=3」の解を加えて拡大した体
`▲
%452:〔§5.2〕(284)/*(Q[x] / (f(x)) `=~ Q(α)*/での追加
`▼
%45P2:〔問5.2〕(284)
%45P3:〔問5.3〕(286)
%45P4:〔問5.4〕(288)
%45T2:〔定理5.2〕(287)/*最小多項式と規約多項式*/
%45T3:〔定理5.3〕(288)/*単拡大体Q(α)の元の表現の一意性*/
%45T4:〔定理5.4〕(291)/*多項式の剰余類群と単拡大体*/
`▲
%45P4:〔問5.4〕(288)
`▼
(0)「2^{1 / 3}」の「`Q[x']」上の最小多項式を求めよ.
(1)参考資料
①〔定理5.2〕(287)
②〔定理5.3〕(288)
③〔定理5.4〕(291) /*「`Q[x'] `=~ Q(α)」*/
④[_最小多項式]@https://ja.wikipedia.org/wiki/最小多項式_(体論)
⑤[3_最小多項式]@http://hooktail.sub.jp/algebra/AlgebraicExtension/
(2)「(0)」の解は「x^{3} - 2」
(3)「Q(i_)」の最小多項式は「x^{2} + 1」
`▲
%453:〔§5.3〕(292)/*Q(α_{1}) `=~ Q(α_{2}), … , `=~ Q(α_{n})*/での追加
`▼
%45P5:〔問5.5〕(294)
%45T5:〔定理5.5〕(292)/*f(x)が引き起こす同型*/
%45T6:〔定理5.6〕(296)/*同型写像と有理関数は順序交換可能*/
%45T7:〔定理5.7〕(296)/*同型写像は解を共役な解に移す*/
%45T8:〔定理5.8〕(297)/*同型写像は解を共役な解に移す:解のシャフル*/
%45T9:〔定理5.9〕(299)/*Q(α_{i})の同型*/
%45TA:〔定理5.10〕(301)/*Q(α)に作用する同型写像はn個*/
`▲
%454:〔§5.4〕(305)/*線形代数の補足*/での追加
`▼
%45P6:〔問5.6〕(312)
%45P7:〔問5.7〕(314)
%45D3:〔定義5.3〕(306)/*線形空間*/
%45D4:〔定義5.4〕(308)/*1次独立・1次従属の定義*/
%45TB:〔定理5.11〕(309)/*1次独立・1次従属*/
%45D5:〔定義5.5〕(310)/*基底の定義*/
%45TC:〔定理5.12〕(311)/*表現の一意性*/
%45TD:〔定理5.13〕(311)/*基底の完全性*/
%45TE:〔定理5.14〕(313)/*Q(α)の基底*/
%45TF:〔定理5.15〕(316)/*線形空間の次元*/
%45D6:〔定義5.6〕(318)/*次元*/
%45TG:〔定理5.16〕(319)/*線形空間の一致*/
`▲
%455:〔§5.5〕(305)/*最小分解体Q(α_{1},…, α_{n})*/での追加
`▼
%45P8:〔問5.8〕(321)
%45P9:〔問5.9〕(322)
%45PA:〔問5.10〕(324)
%45D7:〔定義5.7〕(320)/*最小分解体*/
%45TH:〔定理5.17〕(326)/*同型写像が自己同型写像になる条件*/
%45TI:〔定理5.18〕(329)/*自己同型写像の積も自己同型写像*/
%45TJ:〔定理5.19〕(330)/*自己同型群*/
`▲
%45P8:〔問5.8〕(321)
`▼
(0)「x^{2} - 3」の最小分解体は「Q(3^{1/2})」であることを示せ.
(1)参考資料
①〔定義5.6〕(318)
②〔定義5.7〕(320)
③[_最小分解体]@https://ja.wikipedia.org/wiki/分解体
④[3_最小分解体・代数的閉体]@http://hooktail.sub.jp/algebra/SplitField/
(2)「x^{2} - 3 =(x - 3^{1 / 2}) * (x + 3^{1 / 2})」
(3)
`▲
%456:〔§5.6〕(333)/*中間体*/での追加
`▼
%45PB:〔問5.11〕(333)
`▲
%45PB:〔問5.11〕(333)
`▼
(0)「x^{4} - 4 * x^{2} + 2 = 0」の最小分解体,ガロア群を調べよ.
(1)参考資料
①【[2_45P8](1)】/*「最小分解体」*/
②[_ガロア群]@https://ja.wikipedia.org/wiki/ガロア群
③[3_ガロア群の例]@http://hooktail.sub.jp/algebra/GaloisGroupEx/
(2)最小分解体は〔p.333〕
(3)ガロア群は〔pp.334-338〕
`▲
%457:〔§5.7〕(339)/*2段拡大*/での追加
`▼
%45PC:〔問5.12〕(339)
%45PD:〔問5.13〕(343)
%45PE:〔問5.14〕(344)
%45TK:〔定理5.20〕(348)/*次元の積公式*/
%45TL:〔定理5.21〕(355)/*同型写像の延長*/
%45TM:〔定理5.22〕(358)/*Q(α,β)に作用する同型写像*/
`▲
%45PC:〔問5.12〕(339)
`▼
(0)「x^{4} - 4 * x^{2} + 2 = 0」の最小分解体,ガロア群を調べよ.
(1)参考資料
①【[2_45P8](1)】/*「最小分解体」*/
②[_ガロア群]@https://ja.wikipedia.org/wiki/ガロア群
③[3_ガロア群の例]@http://hooktail.sub.jp/algebra/GaloisGroupEx/
④[3_体の自己同型写像]@http://hooktail.sub.jp/algebra/FieldIsomorphism/
(2)「(0)」の最小分解体は「Q(W`(1 / 3), W`(2 / 3), W`(3 / 3))」
`▲
%45PD:〔問5.13〕(343)`▼
(0)「Q(2^{1 / 2} + 3^{1 / 3}) = Q(2^{1 / 2}, 3^{1 / 3})」を示せ
(2)〔p.333〕の最小分解体は「Q(α, β, γ, δ) ⊂ Q(α)」を満たす.
(3)「Q(α)」の元は「a * α^{3} + b * α^{2} + c * α + d」と表現できる.
(4)「Q」と「Q(α)」の中間にある体を中間体という./*〔p.337〕*/
(5)〔p.340〕のガロア群「Gal(Q(α) / Q)」に対する〔p.342〕の写像 {e, σ, τ, τσ} は
「σ^{2} = τ^{2} = (στ)^{2} = e」を満足し,〔p.343〕の図のように作用する.
(6)「(3)」の「α」の代わりに「W`(1 / 4)」を用いても「W`(K' / 4)」を
「4次元」空間の基底ベクトルに選べる./*「W`(4 / 4) = 1」*/
(7)作用素「σ」,「τ」の作用を復習すると
①「σ(W`(K' / M)) = W`(K'+1) / (M )」
/*「〔p.366〕の『「σ(□)=□」の式が違っているようです」』*/
②「τ(W`(K' / M)) = W`((M - K') / M)」
③「(2)」の最小分解体で考えると〔p.369〕の「Gal(Q(2^{1 / 2}) / Q)」の元は
すべて複素数体上の元に対する演算./*「【[2_5PD]】と同様」*/
(8)「W`(K1 / M)」,「W`(K2 / M)」は複素数体上の元だから自由に四則演算可能.
`▲
%45PE:〔問5.14〕(344)`▼スクロールを減らすために末尾の[%5]に移動しました`▲
%45PF:〔問5.15〕(366)`▼スクロールを減らすために末尾の[%5]に移動しました`▲
%458:〔§5.8〕(360)/*ガロア対応*/での追加
`▼
%45TN:〔定理5.23〕(364)/*固定体*/
%45TO:〔定理5.24〕(365)/*固定群*/
`▲
%459:〔§5.9〕(360)/*Q(α_{1},…, α_{n})=Q(θ)*/での追加
`▼
%45PF:〔問5.15〕(366)
%45PG:〔問5.16〕(370)
%45PH:〔問5.17〕(374)
%45TP:〔定理5.25〕(364)/*原始元の存在*/
%45TQ:〔定理5.26〕(375)/*代数的拡大は単拡大体*/
%45TR:〔定理5.27〕(376)/*最小分解体は単体拡大*/
`▲
%45TQ:〔定理5.26〕(375)/*代数的拡大は単拡大体*/
`▼
(1)「α_{k}」( k ∈ `N(n) )を「`Q[x']」上の方程式「f_{k}(x) = 0」の解とすると
「∃θ,「Q(α_{1}, α_{2},…, α_{n}) = Q(θ)」/*「θ」を原始元という*/
(2)「`Q[x']」上の方程式の最小分解体は「Q(θ)」と表せる/*〔定理5.27〕*/
(3)「(1)」の「α_{k}」,「f_{k}(x)」,「θ」はそれぞれ「W`(k / n)」,「x^{k} - 1」,「W`(1 / n)」.
(4)〔§5.10〕以降はまとめにくいので,〔p.386〕にある要約を「(5)」で紹介して
〔第5章〕の紹介を終わります.
(5)〔p.386〕にある要約の紹介
「Q(α)の同型写像がすべて自己同型写像」
⇔「Q(α)が`Q[x']上の方程式の最小分解体」
⇔「[Q(α)の自己同型写像の個数]=[Q(α):Q]」
⇔「Q(α)が`Q[x']上の正規拡大体」
/*「〔p.387〕の記号G^{M}」は「べき集合」*/
`▲
%45PK:〔問5.20〕(399)
`▼
(0)「α := 2^{1 / 4}」と置いて「x^{4} - 2 = 0」のガロア対応を調べる.
(1)「x^{4} - 2 =(x - α) * (x + α) * (x - i_ * α) * (x + i_ * α)」だから
最小分解体は「Q(α, - α, i_ * α, - i_ * α )」./*「x^{2} + 1」は既約多項式*/
(2)「Q(α, i_)」の基底は「{1, α, α^{2}, α^{3}, i_, i_ * α, i_ * α^{2}, i_ * α^{3}}」
(3)「`G4 := {W`(K / 4); ∈ `N(4)}」と置いて「σ」「τ」を次式で定める
①「σ(W`(K' / 4) := W`((K'+1) / 4))」( K' ∈ `N(4) )
②「τ(W`(K' / 4) := W`((4 - K') / 4))」( K' ∈ `N(4) )
(4)「σ(`G4)=τ(`G4)=`G4」だから「σ」,「τ」は自己同型写像.
`▲
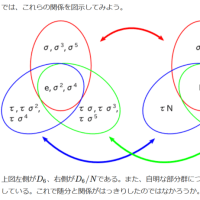
%45TZ2:〔定理5.36〕(406)/*中間体がガロア拡大体になる条件*/
`▼
(0)「`Q」上の方程式「f(x) = 0」の最小分解体を「`L」,そのガロア群を「`G」とする.
(1)参考資料:【[2_45PC](1)】
(2)中間体「`M」と部分群「`H」が対応していれば
「`Mが`Qのガロア拡大体」⇔「`Hが`Gの正規部分群」
(3)「(2)」が成立するとき「Gal(`M / `Q) `=~ `G / `H」/*【「2_2](5)】*/
`▲「本文は、30000文字以下にしてください」になったので〔§5.10〕以降の抄録を割愛
%45ZZ:抄録終了
%5:らくがき/*目次なしで随時挿入*/
%55PE:〔問5.14〕(344)
`▼
(0)「Q(2^{1 / 2}, 3^{1 / 2})」の元は
「a * 2^{1 / 6} + b * 2^{1 / 2} + c * 2^{1 / 3} + d」({a, b, c, d} ⊂ `Q)の形で
一意に表現できることを示せ
(1)参考資料:【[2_45P8](1)】
(2)「x1 := W`(k1 / 2)」「x2 := W`(k2 / 3)」( {k1, k2}⊂`N )と置いて四則演算すると
①x1 + x2 = W`(3 * k1 / 6) + W`(2 * k2 / 6)
②x1 - x2 = W`(3 * k1 / 6) - W`(2 * k2 / 6)
③x1 * x2 = W`(3 * k1 / 6) * W`(2 * k2 / 6) = W`((3 * k1 + 2 * k2) / 6)
④1 / x2 = W`((6 - k2) / 6)
⑤x1 / x2 = x1 * (1 / x2) = W`((3 * k1 - 4 * k2) / 6)
(3)演算結果を「 W`(k3 / 6)」とすると
①「Δ(k3 / 6) ≠ 0」⇒「a ≠ 0」
②「Δ(k3 / 3) = 0」⇒「b ≠ 0」
③「Δ(k3 / 2) = 0」⇒「c ≠ 0」
④「Δ(k3 / 6) = 0」⇒「d = 0」
(4)
`▲[%45PE]から移動
%55PF:〔問5.15〕(366)
`▼
(0)「x^{3} - 2 = 0」の最小分解体とガロア群を調べよ
(1)参考資料:
①【[2_45P8](1)】
②〔定義5.2〕(280)/*「体の同型写像」*/
③[_自己同型写像]@https://ja.wikipedia.org/wiki/自己同型
④[3_体の自己同型写像]@http://hooktail.sub.jp/algebra/FieldIsomorphism/
⑤[_ガロア理論の基本定理]@https://ja.wikipedia.org/wiki/ガロア理論の基本定理
⑥[6_biteki-math]「ガロア対応超入門」@http://biteki-math.hatenablog.com/entry/2015/04/11/224758
⑦[_固定群]@https://ja.wikipedia.org/wiki/群作用#軌道と等方部分群
⑧[3_固定部分群]@http://hooktail.sub.jp/algebra/IsometricGroup/
⑨〔定理5.24〕/*なぜ「σ」と「τ」?*/
⑩〔定理5.23〕/*「固定体」の検索は徒労*/
(2)〔p.372〕の図で「最小分解体の次数=ガロア群の位数」となっていることに注目.
(3)「`Q[x']」と同様の多項式の集合「`R[x']」,「`C[x']」を考える.
①「`R」は実数体,「`C」は複素数体
②「Δ」の非線形性は「`R[x']」で対処できる./*【[%4PB].[%1E1★]】*/
③「代数学の基本定理」により「`C[x'] / (x^{2} + 1) `=~ `C[x']」
④「任意精度の近似で10進表示できる数を実数と考える」
/*【[G6M%2].{実数の計算}】*/
(4)「ω := W`(1/3)」と置いた〔p.366〕の最小分解体の式
「`Q(2^{1 / 3}, 2^{1 / 3} * ω, 2^{1 / 3} * ω^{2}) = `Q(2^{1 / 3), ω)」は
「`C(W`(3 / 3), W`(1 / 3), W`(2 / 3)) = `C(1, ω)」に等しい.
(5)「(0)」のガロア群は〔p.370〕の
①`Q(2^{1 / 3}, ω)/*「2^{1 / 3} ∈ `R」,「ω ∈ `C」*/
②`Q(ω)/*「W`(1 / 3)」:「ω」を含む群は「W`(K' / 3)」( K' ∈ `N(3) )*/
③`Q(2^{1 / 3})/*「2^{1 / 3} * W`(3 / 3)」*/
④`Q(2^{1 / 3} * ω)/*「2^{1 / 3} * W`(1 / 3)」*/
⑤`Q(2^{1 / 3} * ω^{2})/*「2^{1 / 3} * W`(2 / 3)」*/
⑥`Q([x'])/(x^{2} + x + 1)/*「`Q(ω)」*/
(6)「実数体の存在」と「代数学の基本定理」を根拠に
見る「木(定理)」を減らして「森(各章のルート)」が見やすくなるように抄録を作成.
(7)「(1)⑦-⑧」を見ても「固定群」が分かり難いので以下に勝手に推測した具体例を列記.
①巡回群「`G5 := `Δ(K' / 5)'」の元は数平面上の正五角形の頂点「{W`(K/5); K ∈ `N(5)}」に対応.
②「σ(Δ(K' / 5) = Δ((K' + 1) / 5)」「τ(Δ(K' / 5) = Δ((5 - K') / 5)」
③「σ`G5」は正五角形の各頂点を原点を中心にして左回りに「∠`(1/5)」回転する
④「τ`G5」は正五角形の各頂点を「x軸」に関して対称な点に移動する/*「共役な複素数に変換」*/
⑤「σ`G5」が巡回群に対応するように一つの頂点を「(1, 0)」まで回転?
/*「(1)⑧」の正四面体の例を見ると巡回群とは無関係(結晶?)*/
⑥「σ」による「軌跡」とは着目する頂点左隣の頂点に移動する軌跡?
⑦「‘G6 := `Δ(K' / 6)'」には「`Δ(K' / 3)'」に対応する部分群(正三角形)がある./*「固定群?」*/
⑧「σ(W`(K / 5))」( K ∈ `N )の軌道は正多角形上の頂点を移動し,「τ(W`(K / 5))」の軌道は
「y軸」と平行に(周期「2」で「Γ(K / 2)」回)振動する.
`▲[%45PF]から移動
aa