{〔第6章〕の紹介(1)}@https://blog.goo.ne.jp/blogmura-yy/e/f41dce022ad0d7f376cc39ca6dba17f5
/26632+[%56P8M1](茶: 確認中; 灰色: 確認済; 緑: 非慣用記法)/*「確認後白色にする」*/
%0:「〔第6章〕の紹介(1)」
`▼
【[%2].{〔第3章〕の紹介(1)★}】に準じてこのファイルを作成.
`▲
%1:参考資料`▼【[%2].{〔第2章〕の復習(9)}】`▲
%2:資料の参照
`▼
(0)参照の基本形は『「`RefNo[`Site_`ID]」「`Title」@`URL」』
(1)参考資料
①[1_]「〔第5章〕の紹介(1)」@https://blog.goo.ne.jp/blogmura-yy/e/6dc9f9cbb040fe386aafe5307ec1d7c8
②[2_]「このファイル」@https://blog.goo.ne.jp/blogmura-yy/e/f41dce022ad0d7f376cc39ca6dba17f5
③[78_]「ピークの定理への補足」@https://blog.goo.ne.jp/blogmura-yy/e/291675702b4ba0355242fbd4efad28b5
④[79_]「ピークの定理(□)関連資料」@https://blog.goo.ne.jp/blogmura-yy/e/e8b60af195f9178367fb30154bde7914
(2)「③」,「④」は「①」と同じ
(3)「①」を参照しながら「②をオンラインで直接編集」./*「③を使わない」*/
(4)このファイルでは命題「∃f, Imorph`(f; f(S1), S2)」を「S1 `=~ S2」(ゴシック)と略記.
/*【[%414D4](4).[%17]】*/
(5)「~」(ゴシック)を「f^{-1}(x)」の略記「f~(x)」にも使う./*「使用パラグラフで注記」*/
`▲「~」はスマホでは中央に表示される
%21:エディタはフォント指定がない半角文字を「Arial」で表示?
%22:「~」(ゴシック)はスマホでは中央に表示される.
%3:記事の修正`▼【[2_2](4)】`▲/*「[2_2]=[%2].「このファイル」」*/
%4:抄録`▼【[2_2](5)】`▲
%461:〔§6.1〕(412)/*円分方程式の可解性*/での追加
`▼
%46P1:〔問6.1〕(414)
%46T1:〔定理6.1〕(416)/*1のn乗根のべき根表現*/
`▲
%462:〔§6.2〕(422)/*3次方程式をべき根で解く*/での追加
`▼
%46P2:〔問6.2〕(422)
%46P3:〔問6.3〕(423)
%46P4:〔問6.4〕(425)
`▲
%46P3:〔問6.3〕(423)
`▼
(0)「x^{3} + 3 * x^{2} - 3 * x - 11 = 0」を解け.
(1)参考資料
①[_三次方程式]@https://ja.wikipedia.org/wiki/三次方程式
②[3_三次方程式の解の公式]@http://hooktail.sub.jp/algebra/CubicEquation/
③〔問6.4〕(425)の解答
`▲
%463:〔§6.3〕(427)/*べき根拡大*/での追加
`▼
%46P5:〔問6.5〕(427)
%46P6:〔問6.6〕(428)
%46P7:〔問6.7〕(429)
%46P8:〔問6.8〕(432)
`▲
%46P5:〔問6.5〕(427)
`▼
(0)「P(x') := x'^{3} + a * x'^{2} + b * x' + c」( {a, b, c} ⊂ `Q )として
「P(x') = 0」のガロア群を調べよ.
(1)参考資料:/*「[1_45PC](1)のコピー」*/
(2)〔pp.427-428〕の解答の紹介./*「過剰引用を自粛」*/
(3▼)「ω := W`(K' / 3)」を用いた「(2)」の表現
`▲「(3▼)」は「らくがき」だからこのパラグラフ全体を[%5]に移動
%46P8:〔問6.8〕(432)
`▼
(0)「P(x') := x'^{3} + p * x' + q = 0」( {p, q} ⊂ `Q )のガロア群の位数が「6」であるとして
「P(x') = 0」のガロア群を調べよ.
(3▼)「ω := W`(K' / 3)」を用いた「(2)」の表現
`▲「(3▼)」は「らくがき」だからこのパラグラフ全体を[%5]に移動
%464:〔§6.4〕(437)/*4次方程式の解の公式*/での追加
`▼
%46P9:〔問6.9〕(422)
%46PA:〔問6.10〕(423)
%46PB:〔問6.11〕(425)
`▲
%465:〔§6.5〕(441)/*累巡回拡大体*/での追加
`▼
%46PC:〔問6.12〕(441)
%46PD:〔問6.13〕(444)
%46T2:〔定理6.2〕(447)/*可解群と累巡回拡大の対応*/
`▲
%466:〔§6.6〕(453)/*円分体とガロア群*/での追加
`▼
%46PE:〔問6.14〕(453)
%46PF:〔問6.15〕(455)
%46PG:〔問6.16〕(457)
%46PH:〔問6.17〕(458)
%46PI:〔問6.18〕(459)
%46T3:〔定理6.3〕(457)/*円分体のガロア群*/
`▲
%467:〔§6.7〕(463)/*クンマー拡大*/での追加
`▼
%46PJ:〔問6.19〕(463)
%46PK:〔問6.20〕(463)
%46PL:〔問6.21〕(470)
%46PM:〔問6.22〕(470)
%46T4:〔定理6.4〕(467)/*べき根拡大から巡回拡大を作る*/
`▲
%468:〔§6.8〕(472)/*巡回拡大からべき根拡大へ*/での追加
`▼
%46T5:〔定理6.5〕(473)/*巡回拡大からべき根拡大を作る*/
%46T6:〔定理6.6〕(476)/*デデキントの補題*/
%46T7:〔定理6.7〕(478)/*べき根拡大を作るべき根の存在*/
`▲
%46T7:〔定理6.7〕(478)/*べき根拡大を作るべき根の存在*/
`▼
(0)「ζ」を「1」の原始n乗根とし,「g(x) := x + ζ^{n - 2} * σ(x) + ζ^{n - 1} * x」とする.
/*「σ(x) = σ^{1}(x)」,「x = σ^{n}(x)」( n = (n - 1) + 1) )*/
(1)集合「{g(θ^{k}); k ∈ `N(n - 1)}」には/*【定義から当然】*/「σ^{n}(x)」は含まれない.
(2)「連立1次方程式」や「ファンデルモンドの行列式」を用いるともっとあざやかに【証明】できますが
線形代数の知識が必要」〔p.479〕
(3▼)「`C[x']」で考えると「ζ = W`(1 / n)」,「g(θ^{k}) = W`(k / n)」( k ∈ `N(n) )
`▲パラグラフ全体を【%56T7】に移動
%469:〔§6.9〕(480)/*べき根で解ける方程式の条件*/での追加
`▼
%46T8:〔定理6.8〕(480)/*可解群のとき解はべき根で表される*/
%46T9:〔定理6.9〕(481)/*累べき根拡大体のガロア閉包*/
%46TA:〔定理6.10〕(486)/*解がべき根で表されるときは可解群*/
`▲
%46T9:〔定理6.9〕(481)/*累べき根拡大体のガロア閉包*/
`▼
(0)〔定理6.8〕の逆の命題./*「ピークの定理の完結」*/
(1)「α」がべき根で表されているとき,「`E / `Q」が累巡回拡大かつガロア拡大となる
「α」を含む「`Q」の拡大体が存在する
(2)〔pp.481-486〕の説明の紹介
(3)
(4)
`▲作業中
%46A:〔§6.10〕(488)/*ガロア群が可解群でない方程式*/での追加
`▼
%46PN:〔問6.23〕(491)
%46TB:〔定理6.11〕(488)/*位数pの元の存在-コーシーの定理*/
`▲
%46PN:〔問6.23〕(491)
`▼
(0)「x^{5} - 6 * x + 3 = 0」の解はべき根で表せないことを示せ.
(1)参考資料
①[アーベル-ルフィニの定理]@
https://ja.wikipedia.org/wiki/アーベル-ルフィニの定理
②[五次方程式]@
https://ja.wikipedia.org/wiki/五次方程式
③[5次方程式が解けないことの直感的説明]@
http://yosniimura.net/memo/quintic_equation.html
④[群論からガロア理論への入門(五次方程式の解の公式は存在しない)]
https://math-fun.net/20191210/3949/
⑤[5次方程式の解]@
https://www.geisya.or.jp/~mwm48961/linear_algebra/algebra_eq5.htm
⑥[20歳で逝った天才数学者が残した理論とは]@
https://news.livedoor.com/article/detail/17295601/
⑦[5次方程式解の公式]@
http://www.isc.meiji.ac.jp/~kurano/soturon/ronbun/07kurano.pdf
⑧[4次方程式と5次以上の方程式の Galois 理論]@
https://www.kaijo.ed.jp/wp-content/uploads/2016/02/2011summer_6Amitani.pdf
(2)
(3)
`▲
%46Y:あとがき
`▼
(1)高校生にも分かり易いように〔第1章〕から複素数を使いました
(2)【[1_55PF](6)】の方針に不満を感じる高校生は大学に進学してから原著を読み直してください
/*「工学部に進学しても〔第3章〕や〔第4章〕は役立ちます」*/
(3)5月は「〔第2章〕の復習(9)」のコピーに加筆して「ピークの定理(17)」を作成.
(4)6月に「ep58-kit」が「WILDの処理系」を開始.
(6)「アクセス解析」のデータに励まされて〔第6章〕に辿り着きました.皆様に感謝!
・紹介-8; 紹介-9
`▲
%46Z:抄録終了
%5:らくがき
%56P5:〔問6.5〕(427)
`▼
(0)「P(x') := x'^{3} + a * x'^{2} + b * x' + c」( {a, b, c} ⊂ `Q )として
「P(x') = 0」のガロア群を調べよ.
(1)参考資料:/*「[1_45PC](1)のコピー」*/
①〔定義5.6〕(318)
②〔定義5.7〕(320)
③[_分解体]@https://ja.wikipedia.org/wiki/分解体
④[3_最小分解体・代数的閉体]@http://hooktail.sub.jp/algebra/SplitField/
⑤[_ガロア群]@https://ja.wikipedia.org/wiki/ガロア群
⑥[3_ガロア群の例]@http://hooktail.sub.jp/algebra/GaloisGroupEx/
⑦[3_体の自己同型写像]@http://hooktail.sub.jp/algebra/FieldIsomorphism/
(2)〔pp.427-428〕の解答の紹介./*「過剰引用を自粛」*/
①〔問6.3〕と同様に「x := X - a / 3」と変数変換して「X^{2}」のない式を作り
「P(X) = 0」の解を「{α_{1}, α_{2}, α_{3}}」とすると
「Q(α_{1}, α_{2}, α_{3}) = Q(α_{1} - a / 3, α_{2} - a / 3, α_{3} - a / 3)」
②「x^{3} + p * x + q = 0」の解を「{α, β, γ}」とすると,
これらは「t^{2} + q * t + p^{3} / 27 = 0」の解を「{u^{3}, v^{3}}」として
「α = u + v」,「β = ω * u + ω^{2} * v」,「γ = ω^{2} * u + v」と表現できる
③3次方程式の根と係数の関係から
「α + β + γ = 0」,「α * β + β * γ + γ * α = p」,「α * β * γ = - q」.
/*「(x - α) * (x - β) * (x - γ) = x^{3} + p * x + q」*/
④「③」の「p」,「q」は有理数である./*〔pp.427-428〕*/
(3)「W`(K' / 3)」を使うと/*「u = W`(1 / 3)」,「v = W`(2 / 3)」*/
①「x^{3} - 1 = (x - W`(1 / 3)) * (x - W`(2 / 3)) * (x - W`(3 / 3))」,「W`(3 / 3) = 1」
②「W`(K'/3) = cos(∠(K' / 3)) + i_ * sin(∠(K' / 3))」( K' ∈ `N(3) )」/*「∠(3 / 3) = 2 * π」*/
③「W`(2 / 3)」は「W`(1 / 3)」と共役な複素数.
④「γ = 1」,「α + β = - 1」,「α * β = 1」だから
「(x - α) * (x - β) * (x - γ) 」
=「x^{3} + (α + β + 1) * x^{2} + (α * β + α + β) * x - (α * β * 1)」
=「x^{3} - 1」
(4)「∠`(K' / M)」は無理数だから「W`(K1 / M)」を使った段階で「`C(x')」による考察.
/*「`Q[x'] ⊂ `R[x'] ⊂ `C[x']」で,主役は原始根「W`(1 / M)」*/
`▲[%46P5]から移動
%56P8:〔問6.8〕(432)
`▼
(0)「P(x') := x'^{3} + p * x' + q = 0」( {p, q} ⊂ `Q )のガロア群の
位数が「6」であるとして「P(x') = 0」のガロア群を調べよ.
(1)参考資料
①[_べき根]@https://ja.wikipedia.org/wiki/冪根
②[_べき根拡大]@https://ja.wikipedia.org/wiki/冪根#冪根拡大
③[3_累開冪拡大体の列]@http://hooktail.sub.jp/algebra/RadicalTower/
④〔問6.8〕の解説〔pp.425-436〕
(2)「(1)④」の拡大体の式を紹介する
①「1」の原始n乗根のべき根は「cos(∠`(1 / n)) + i_ * sin(∠`(1 / n))」./*〔p.413〕*/
②「x^{2} + x + 1 = 0」の一つの解を「ω」とする./*〔p.427〕*/
③「η := q^{2} / 4 + p^{3} / 27」( (p, q) ∈ `Q)として「x^{2} - η = 0 」から
「Q(ω, η^{1/2})」を作る
④「θ := q / 2 + η^{1/2}」として「x^{3} - θ = 0 」から
「Q(ω, η^{1/2}, θ^{1/3})」を作る.
⑤「η」が有理数でないとき「Q(α, β, γ)」は「`Q[x']」の「6次拡大」だから
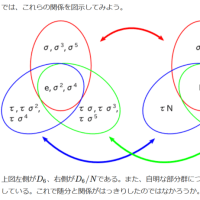
ガロア群の位数は「6」./*〔p.433〕の「ガロア対応図」*/
⑥「べき根拡大だけで解を含む体を作ろうとしたらωを使わざるを得なかった」〔p.435〕は難解.
/*「高校生は気にせず,次項以降を見て考えてください」:【[1_55PF](6)】*/
(3)「 W`(θ' / M)」を用いた「(2)」の表現
①「q^{2}」「p^{3}」を「W`(K' / M)」で表したいので「`G(M) := {W`(K / M); K ∈ `N(M)}」と定義.
②【[2_2](4)】の「S1 `=~ S2」(ゴシック)を使用.
③【[1_45PK](3)】を一般化した次の作用素「σ」,「τ」を使う
「σ(W`(K' / M) ::= W`((K' + 1) / M))」( K' ∈ `N(M) )
「τ(W`(K' / M) ::= W`((M - K') / M))」( K' ∈ `N(M) )
④「σ(`G(M)) = τ(`G(M)) = `G(M)」
⑤「W`(K' / M) + W`((M - K') / M) = 0」,「W`(K' / M) * W`((M - K') / M) = 1」/*「逆元が存在」*/
(4)「(2)③」より簡単な「`Q(2^{1 / 2}, 3^{1 / 2))」による考察
①最小多項式「x^{2} - 2」の「`R[x']」での因数分解は「x^{2} - 2 = (x - 2^{1 / 2}) * (x + 2^{1 / 2})」
②「`Q(2^{1 / 2}, 3^{1 / 2))」の元は
「θ * W`(K' / 4)」( θ ∈ `Q(2^{1 / 2}, 3^{1 / 2)) )と表現できる./*「K' ∈ `N(4)」*/
③
(5)「(2)②」の「Q(ω)」( ω^{3} = 1 )の拡大に関する考察
①「x^{5} - 7」の「`C[x']」での因数分解は「(7^{1/5}) * (x - 1) *(x^{4} + x^{3} + x^{2} + x + 1)」
②原始多項式「x^{4} +x^{3} + x^{2} + x + 1」の原始根は「W`(1 / 5)」
③「Q(ω, η)」( η = 7^{1 / 5} )の元は「η * W`(K / 15)」( K ∈ `N(15) )と表現できる
④「W`(k / 15)」( k < 7 )の虚数部は非負,「W`(k / 15)」( k > 8)の虚数部は負.
⑤
(6)「W`(K1' / 15)」,「W`(K2' / 15)」は「`C[x']」で自由に四則演算可能.
(7) 【[1_55PF](6)】の『「実数体の存在」と「代数学の基本定理」を根拠に
見る「木(定理)」を減らして「森(各章のルート)」が見やすくなるように抄録を作成.』への補足.
①「実数の存在」は実数「x」を超えない最大の整数「Γ(x)」が一意に定まること.
/*「x」と大きさを比較して「Δ(x) := x - Γ(x)」と定義できる.*/
②「代数学の基本定理」は「`C[x']」上の多項式は「(x - W`(k / n))」( k ∈ `N(n) )の積に
因数分解できること./*定義を変えずに「W`(θ / n)」( θ ∈ `N(n) )を使える*/
③「`C[x']」上の多項式は自由に四則演算可能./*「複素数の定数は「0次」の多項式」*/
(8)正規列の例./*【[%64P3].[%127]】*/
`▲[%46P8]に加筆
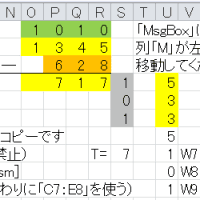
%56P8M1:〔問6.8〕に関するらくがき
`▼
(0)【[%56P8]】に関する無責任メモです
(1)『「`K」が「1」の原始根「ζ」を含むときべき根拡大K(a^{1 / n})は巡回拡大である』〔p.468〕
の 「`K」は複素数体「`C」であるとして次のように解釈する.
①「ζ = W`(1 / n)」
②任意の正の実数「x」に対して「x^{n} = a」となる「x」を「a^{1 / n}」〔p.468〕と表記.
/*「a」は円周率や自然対数の底でもよい」*/
③「数平面」上の点「r * (cos(∠`(k / n)) + i_ * sin(∠`(k / n)))」( r > 0 )と
単位円上の点「r^{1 / n} * W`(k / n)」は1対1に対応する.
④複素数体の元「r^{1 / n} * W`(k' / n)」( (n, k') ∈ `N × `Z )は自由に四則演算可能.
⑤「`G_{n} := {W`(k / n); k ∈ `N(n)}」は位数「n」の巡回群と同型
⑥「`G_{n}」に加法と乗法の逆元/*【[2_56P8](3)⑤】*/が存在するので体になる.
(2)〔定理6.4〕(467)に興味がある高校生はまず「商群」(「索引」に不在)について学び,
「Gal(K(a^{1 / n})/`K)」の意味を知ることが不可欠.
/*「https://note.com/noppoman/n/nb4bd7142700b」*/
(3)「数平面」上の原点を中心とする単位円に内接する正n角形を回転して
一つの頂点を「1」に置くと「対称群」から離れて幾何学的に考察できる.
①「x^{2} - 1 = (x - 1) * (x + 1)」
②「x^{3} - 1 = (x - 1) * (x^{2} + x + 1)」
③「x^{4} - 1 = (x^{2} - 1) * (x^{2} + 1)」
④「x^{5} - 1 = (x - 1) * (x^{4} + x^{3} + x^{2} + x + 1)」
⑤「x^{2} + x + 1 = 0」の根の計算で「W`(1 / 3) - W`(2 / 3) = 2 * 3^{1 / 2}」
⑥「x^{2} + 1 = 0」の根の計算で「x^{2} + 1 = (x - i_) * (x + i_)」
(4)「`R[x']」上の既約でない4次方程式「③」から虚数単位「i_」を定義したのと同様に
適当な既約でない5次方程式から「i5_」を定義すれば5次方程式も代数的に解ける.
`▲「(4)」に駄文を追加するとすぐに「30000字」を超えるので別ファイルで紹介.
%56T7:〔定理6.7〕(478)/*べき根拡大を作るべき根の存在*/
`▼
(0)「ζ」を「1」の原始n乗根とし,「g(x) := x + ζ^{n - 2} * σ(x) + ζ^{n - 1} * x」とする.
/*「σ(x) = σ^{1}(x)」,「x = σ^{n}(x)」( n = (n - 1) + 1) )*/
(1)集合「{g(θ^{k}); k ∈ `N(n - 1)}」には/*【定義から当然】*/「σ^{n}(x)」は含まれない.
(2)「連立1次方程式」や「ファンデルモンドの行列式」を用いるともっとあざやかに【証明】できますが
線形代数の知識が必要」〔p.479〕
(3▼)「`C[x']」で考えると「ζ = W`(1 / n)」,「g(θ^{k}) = W`(k / n)」( k ∈ `N(n) )
/*「g(x):= W`((n - 1) / n) + W`((n - 2) / n) + …, + W`(n / n)」*/
(4)方程式「W`(x / n) = 0」( x ∈ `C )の解/*【準同型の核の元】*/は「x = 1」.
`▲作業中【%46T7】に加筆
aa