{〔第2章〕の復習(7)}@https://blog.goo.ne.jp/blogmura-yy/e/db7541e83f506a504199fa715a513b12
作業中/26069+[%64P1](茶: 確認中; 灰色: 確認済; 緑: 非慣用記法)
/
・[1_6]が「25000字」を超えたので [1_7]を作成して【[2_64]以降を移動】
・更新されないパラグラフがあるのでファイルを削除して新規に作成.
%70:複素数で考える商群
・「異端爺」のメモ.無理数【π】を用いて分数を使わない「正統派」の説明【整数論の入門書】に反抗.
・「30000字」対策で[1_64]以降をこのファイルに移動.
%701:参考資料`▼[1_601]のコピー`▲
%702:記事の参照`▼[1_602]のコピー`▲
%703:目次
`▼
%61:1次不定方程式
%62:有限体
%63:既約多項式
%64:ユークリッド空間
%65:剰余類
%66:部分群
%67:準同型写像
%71:多項式環
%72:正規部分群
%73:商群
%74:可解群
`▲「灰色のパラグラフ別ファイル」
%64:部分群
%64D1:記号の定義/*「部分群」*/
`▼
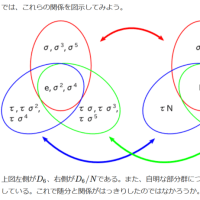
(1)「`Δ(Δ(K' / 3))'」( K' ∈ `N(3) )が「`Δ(K' / 6))'」( K' ∈ `N(6) )の部分集合
であることを「`Δ(K' / 6))'⊃`Δ(Δ(K'/ 2) / 3))'」( K'∈ `N(6) )と表記./*「式」( 式への制約条件 )*/
(2)「`Δ(K' / M)' = {Δ(K / M); (K ∈ `N(M))∧(GCD`(K, M) = 1)}」である「剰余類」を「既約剰余類」といい
「`Δ(K' / M)"」と略記する/*「非慣用記法」*/
(3)「`Δ(K' / 6))'⊃`Δ(Δ(K'/ 2) / 3))'」( K'∈ `N(6) )を「正規列」という
(4)参考資料
①[_剰余類環]@https://ja.wikipedia.org/wiki/剰余類環
②[63_既約剰余類群]@http://biteki-math.hatenablog.com/entry/2015/04/14/135722
③[_群論の用語#正規列]@https://ja.wikipedia.org/wiki/群論の用語#正規列
④[_正規部分群]@https://ja.wikipedia.org/wiki/正規部分群
⑤[3_正規部分群]@http://hooktail.sub.jp/algebra/NormalSubgroup/
⑥[_組成列]@https://ja.wikipedia.org/wiki/組成列
⑦[3_組成列]@http://hooktail.sub.jp/algebra/GroupSeries/
(5)「`Δ(K' / 6))'⊃`Δ(Δ(K'/ 2) / 3))'⊃`Δ(Δ(K'/ 3) / 2))' ⊃ `Δ(Δ(K'/ 1) / 1))'」は組成列
/*「`Δ(Δ(K'/ 1) / 1))'=`Δ(0 / 1))' = {0}」*/
(6)「`GR(M)={Δ(K / M); (K ∈ `Z)∧(K < M)}」,「GR`[K']=Δ((K'- 1) / M)」( K' ∈ `N(M) )と定める
(7)例えば
①「`GR(6) = {Δ((K - 1) / 6); K ∈ `N(6)}」
②「`GR(3) = {Δ(1 / 3), Δ(2 / 3), Δ(3 / 3)}」
③「`GR(2) = {Δ(1 / 2), Δ(2 / 2)}」
④「`GR(1) = {Δ(1 / 1)} = {0}」
⑤「`GR(6) ⊃ `GR(3) ⊃ `GR(2) ⊃ `GR(1)」
`▲「(2)」を修正./*「背景色はオプション」*/
%64P1:〔問4.1〕/*「同型写像」*/
`▼
(0)[2_64D1](7)の「`GR(K')」に対して「f(`GR(6)) = `GR(3)」となる「同型写像 f」を求めよ.
/*「f(`GR(6)) = {f(X); X ∈`GR(6)} 」*/
(1)参考資料
①[_部分群]@https://ja.wikipedia.org/wiki/部分群
②[_同型写像]@https://ja.wikipedia.org/wiki/同型写像
③[3_準同型写像]@http://hooktail.sub.jp/algebra/Homomorphic/
④[_代数的構造]@https://ja.wikipedia.org/wiki/代数的構造
(2)「f(Δ(K' * 2) / 6) = {Δ(2 / 6),Δ(4 / 6),Δ(6 / 6)} = `GR(3)」( K' ∈ `N(6) )
/* 「{a, b, a, a, b} = {a,b}」*/
(3)「Δ(K' / 6)」( K'∈ `N(6) )に対応する「_xy平面」上の正六角形「{P`(K' / 6)}」の
正三角形「{P`(K' / 3)」( K'∈ `N(3) )と合同な正三角形は
①「{P`(2 / 6), P`(4 / 6), P`(6 / 6)}」,「{P`(1 / 6), P`(3 / 6), P`(5 / 6)}」
②「{P`(1 / 6), P`(3 / 6), P`(5 / 6)}」は「P`(K' / 3)」( K'∈ `N(3)を原点の周りを
「360°/ 2」( 2 = 6/3 )回転した点とみなすと考えやすい.
③「Δ(K' / 24)」( K'∈ `N(24) )の場合は「360°/ 8」( 8 = 24/3 )回転
/*合同な正三角形は「8」個*/
(4)一般に「Δ((M - K') / M)」=1-Δ(K' / M)」( K'∈ `N(M) )
/*「Δ((M - K') / M)」は「Δ(K' / M)」の加法の逆元./*【[1_63D1](5)】*/
(5)「f(`Δ(K'/ 6)')=`Δ(K3'/ 3)'」( (K', K3') ∈ `N(6)×`N(3) )/*「f(Δ(K'/ 6) = Δ((K' * 2) / 6)」*/であれば
「`Δ(K'/ 6)'」と「`Δ(K'/ 3)'」は「代数的構造」が等しい.
①巡回シフトの作用素「σ」/*【[2_63D1](1)】*/に対しても次式が成立:
「σ`Δ(K'/ 6)' = σ`Δ(K3'/ 3)'」
(6)
`▲「f」の背景色を修正
%64P2:〔問4.2〕/*「平方根の計算」*/
`▼
(0)「_xy平面」の点「(P[1], P[1])」( P[1]=2 )と原点「(0, 0)」を結ぶ線分を対角線とする正方形を
「S[2]」とし,この対角線と「(P[1], P[1])」を中心とする半径「P[1]」の円の交点の座標を
「(P[2], P[2])」とする./*P[2] = (2^{1 / 2} - 2」*/
(1)「(P[1], P[1])」と「(0, 0)」を結ぶ線分の長さは「2^{1 / 2}」
(2)「(P[K'], P[K'])」と原点「(0, 0)」を結ぶ線分を対角線とする正方形を「S[K' + 1]」
としてこの対角線と「(P[K'], P[K'])」を中心とする半径「P[K']」の円の交点の座標を
「(P[K'+ 1 ], P[K'+ 1])」とする./*「P[K' + 1] = (2^{1 / 2}) - P[K']」*/
(3)点「(P[K'], P[K'])」は「K'」の増加に伴って原点に近づき「K' → ∞」の極限で「(0, 0)」に収束.
`▲
%64P3:〔問4.3〕/*「立方根の計算」*/
`▼
(0)「_xyz空間」の点「(P[1], P[1], P[1])」( P[1] = 2 )と原点「(0, 0, 0)」を結ぶ線分を
対角線とする立方体を「V[1]」とし,この対角線と「(P[1], P[1], P[1])」を
中心とする半径「2」の球の交点を「(P[2], P[2], P[2])」とする.
(1)「(P[1], P[1], P[1])」と「(0, 0, 0)」を結ぶ線分の長さは
「((P[1] - 0)^{2} + (P[1] - 0)^{2} + (P[1] - 0)^{2})^{1/2} = (2^{2} * 3)^{1/2}」
(2)「(P[K'], P[K'], P[K'])」と原点「(0, 0, 0)」を結ぶ線分を対角線とする立方体を「V[K' + 1]」
としてこの対角線と「(P[K'], P[K'], P[K'])」を中心とする半径「P[K']」の円の交点の座標を
「(P[K'+ 1 ], P[K'+ 1], P[K'+ 1])」とする./*「P[K' + 1] = (12^{1 / 2}) - P[K']」*/
(3)点「(P[K'], P[K'], P[K'])」は「K'」の増加に伴って原点に近づき「K' → ∞」の極限で
「(0, 0, 0)」に収束.
(4)「(P[K'], P[K'], P[K'])」と「(0, 0, 0)」を結ぶ線分を対角線とする正六面体を「V[K']」とすると
「V[K'] ⊃ V[K' + 1]」だから
「正六面体群」/*【[1_63D2](4)⑤】*/の「正規列」/*【[1_64D1](4)③】*/を作れる.
`▲「(2)」を訂正
%64P4:〔問4.4〕/*「べき乗根の計算」*/
`▼
(0)「4次元ユークリッド空間」の点「(P[1], P[1], P[1], P[1])」( P[1] = 2 )
と原点「(0, 0, 0, 0)」を結ぶ線分を対角線とする「超立方体」を「V[1]」とし,
この対角線と「(P[1], P[1], P[1], P[1])」を中心とする半径「2」の「超球面」の
交点を「(P[2], P[2], P[2], P[2])」とする.
①[_ユークリッド空間]@https://ja.wikipedia.org/wiki/ユークリッド空間
②[3_四次元の世界]@http://hooktail.sub.jp/welcome/what4dim/
③[_超立方体]@https://ja.wikipedia.org/wiki/超立方体
④[_超球面]@https://ja.wikipedia.org/wiki/超球面
(1)「V[1]」の対角線と「(P[K'], P[K'], P[K'], P[K'])」を中心とする半径「2」の「超球面」の
交点を「(P[K' + 1], P[K' + 1], P[K' + 1], P[K' + 1])」とする.
(2)「(P[1], P[1], P[1], P[1])」と「(0, 0, 0, 0)」を結ぶ線分の長さは
「 (2^{2} * 4)^{1/2}」
(3)点「(P[K'], P[K'], P[K'], P[K'])」は「K'」の増加に伴って原点に近づき「K' → ∞」の極限で
「(0, 0, 0, 0)」に収束.
`▲
5:準同型写像
%65D1:記号の定義/*「準同型写像」*/
`▼
(1)慣用記法に反する次の記号を定義する
①写像「f1:`R → `R」,「f2:`R → `R」の「合成写像★」を「(f1)・(f2)」で表す/*「非慣用記法」*/
/*「□・□」を別の用途で使用*/
②「(f1・f2)」が「恒等写像」となる「f1」/*「逆写像」*/が存在すれば
これを「f2~」と略記./*ゴシックにすると(上付)「~」になる*/.
③「虚数単位★」を「i_」,「自然対数の底★」を「e_」と表記/*「緑は定義行のみ」*/
④「x」の「自然対数」を「log(x)」,「常用対数」を「log10(x)」と略記
「log(1) = e_」だから「e_^{i_ * x} = exp(i_ * x)」
(2)「準同型写像」の参考資料
①[_群準同型#準同型写像]@https://ja.wikipedia.org/wiki/群準同型#準同型写像の種類
②[3_準同型写像]@http://hooktail.sub.jp/algebra/Homomorphic/
③[_準同型定理]@https://ja.wikipedia.org/wiki/準同型定理
④[4_準同型定理]@http://www.f-denshi.com/000TokiwaJPN/01daisu/120gun.html
⑤[_自然変換]@https://ja.wikipedia.org/wiki/自然変換
⑥[61_]「群の自然な準同型と部分群の対応」@http://peng225.hatenablog.com/entry/2016/12/18/112359
⑦[93_]「"自然な"の意味」@https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14169193324
/*「たいてい次のどちらかだと思います」:
「部分群(部分対象)からの標準的単射」/「剰余群(商対象)への標準的全射」*/
(3)「⑦部分群からの標準的単射」の例は/*【[2_64P1](3)②】*/
(4)「⑦剰余群への標準的全射」の具体例による説明の紹介/*【[2_65D1]⑥】*/
`▲「(1)」の背景色を修正
「(2)-(4)」を更新
aa