前回、突然にペンローズ・ダイアグラムすなはちペンローズ図を持ち出したため、話がいきなり難解になってしまい、誠に失礼しました。
それで、このペンローズ図について易しく説明をしてくれている書籍を探したのですが、専門書以外にはあまり一般に出回っていなくて、私の書棚からペンローズ関連の書物を探してみました。
すると、講談社のブルーブックに「ペンローズのねじれた四次元」という竹内薫氏がお書きになっている本が見つかりました。
今回は、「ペンローズ図とは?」という題でブログに書かせていただきます(ほとんど抜粋編集)。ただし、この書籍から、ペンローズ図に必要な部分を抜き出しています。いくらかでも時空構造を理解するための、手助けになってくれたらいいなと思っています。
ペンローズ図というのは、無限に遠い所を有限の所にもってきた図のことを言う。ペンローズ以前には、この図を描いた人はいなかったわけだから、この発明は、実は、大変なことなのだ。 普通の時空図をペンローズ図に変換する数式は、ものすごく複雑で、かなり数学をやった人でも、「どうして、こんな変換に気がついたのか!」と悲鳴をあげるに違いない。
一般相対論の教科書のバイブルとして有名で「電話帳」の異名を取る「Gravitation]
という分厚い本には、ペンローズ図について、次のような記述がある。ペンローズは一般相対論の業績があまりにも多く、他人が思いつかないような図を描くので、どれもこれも「ペンローズ図」になってしまう、というわけ。
ところで、なんで無限の点を有限のところにもってくる必要があるのか?
実は、それには、れっきとした物理学的な理由がある。
ここでは、技術的な問題に深入りはできないが。結論から言うと、ハーマン・ボンディやペンローズらによって、うまい方法が考えだされた。ペンローズ図は、そのような物理学者たちの重力場との悪戦苦闘の過程で生れたのであった。
それでは、ペンローズ図の読み方を伝授しよう。
この図の見方は、おそらく、物理学者でもわからない人がいるのだと思う。といっても、いくつかの決まりさえ覚えれば、そんなに難しいものでもない。メルカトル図法の地図を平気で読んでいる人なら、大丈夫、読める。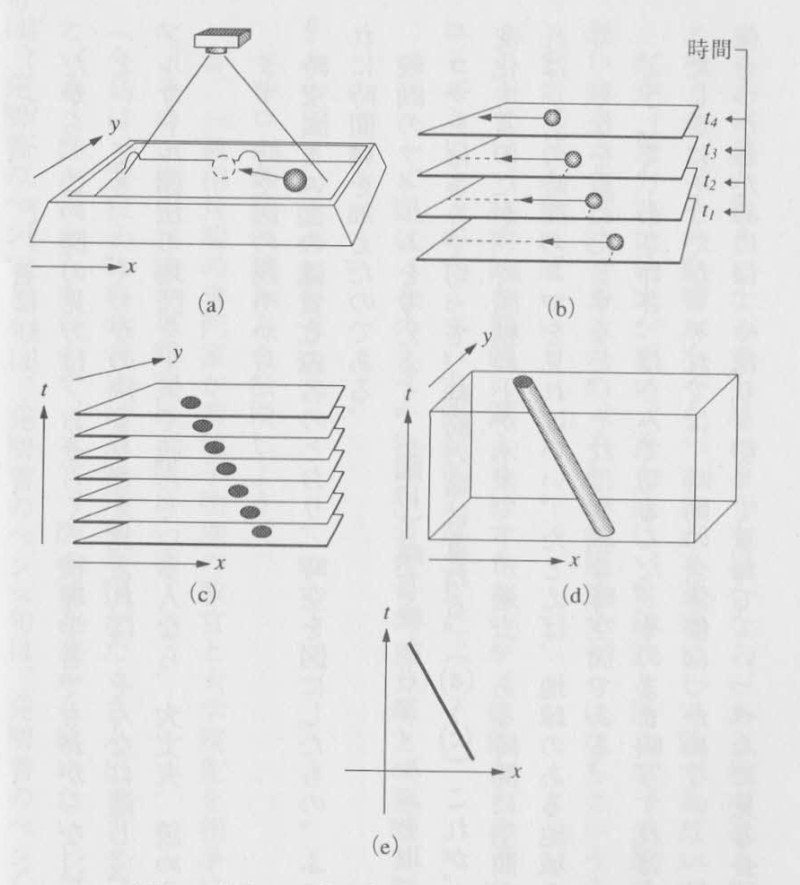
図1:フィルムの重ね図
まず、時空図の説明から始めよう。時空図というのは、その名のとおり、時空を図にしたもの。ふつうの地図は、空間図だが、それに時間軸を加えたのである。
映画のフィルムを考えよう(図1)。映写機からフィルムを取ってきて、フィルムの一コマ、一コマをはさみで切って、時間の順に重ねる((a)~(c))。これが、時空図である。空間の様子が変化するのだが、時間軸の上が未来で下が過去。
ある時間に空間がどうなっているかを知りたければ、その時間のコマを見ればいい。たとえば、地球のある地域の歴史をフィルムに撮っておいて、それを重ねたとすると、それは立派な時空図である。
もっとも、フィルムの場合、四角形なので、二次元になっていて、図が見づらい(d)。そこで、多くの場合、二次元のフィルムの軸を一つだけ残して、単純化する。だから、時間軸のほかには、空間軸が一つだけになる。通常は、縦軸が時間で横軸が空間だ(e)。
時空図は、上下左右に無限に大きいと考える。
ここで、原点にある電球から四方に照射された光がどう描かれるかに注目してほしい。光は、時間とともに遠くまで達する。光速は約30万キロメートル毎秒だから、時間軸の目盛りを1秒、空間の目盛りを30万キロメートルにしておけば、光は、傾きがプラス・マイナス1の直線として表される。角度が45度である。
この光の軌跡のことを「光円錐」(Light cone)と呼ぶ。どうしてかというと、フィルムの空間次元をもとの二次元に戻すと、光が原点から円錐状に出ているから(図2)。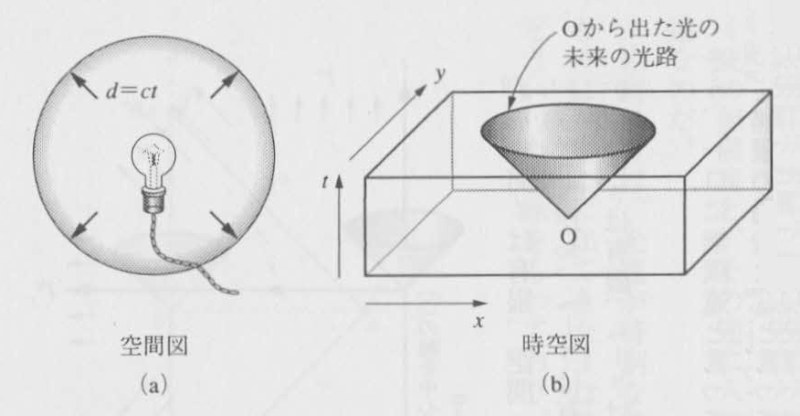
図2:光円錐の図
それでは、いよいよペンローズ図である。
普通の時空図は、アインシュタインのチューリッヒ工科大学時代の数学の先生であったヘルマン・ミンコフスキーの名をとって、「ミンコフスキー図」と呼ばれている。このミンコフスキー図では、無限遠は無限遠にあるので、紙の上に描いたのでは見えない。無限遠で時空がどうなっているかは見ることができないのだ。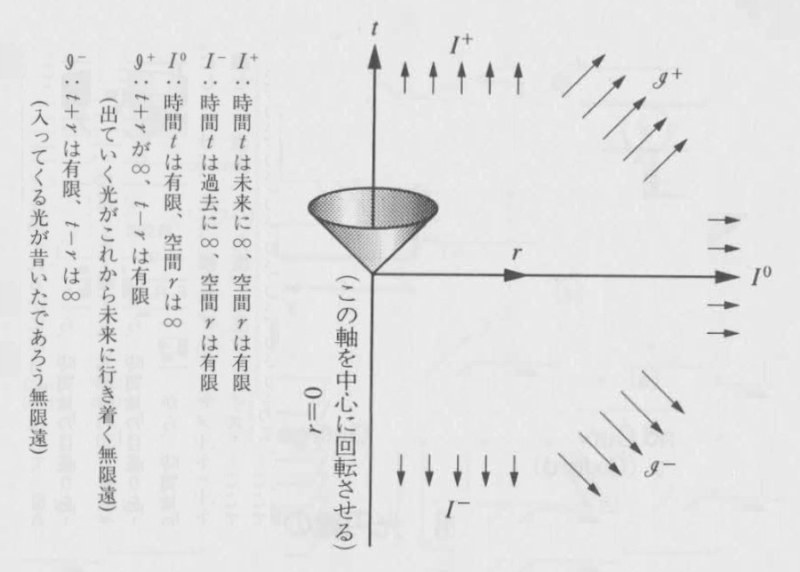
図3:ミンコフスキー図
平らな時空のミンコフスキー図には、いくつかの重要な無限遠の方向がある(図3)。そう、一口に無限遠と言っても。どっちの方向に遠いかで話が変わってくる。ここで、無限の未来と無限の過去と空間的な無限遠はいいとして、最後の二つがくせものだ。これは、無限の未来と空間の無限遠(右斜め上方向)と、無限の過去と無限遠の空間(右斜め下方向)だ。原点から出ていく光が行き着く先の無限遠と、その逆に入ってくる光が出発した無限遠である。二つとも、光にとっての無限遠なのだ。
相対論では、光速が特別な役割を演ずるため、「光の観点からの無限」を考えるのである。ちなみに、ここに出てきたIは英語のinfinity(無限)の頭文字で、肩の添え字は、未来(+)、過去(-)などといった意味をもっており、最後の二つの文字は「スクリー」と読む。時空の無限は、未来、過去、空間、二つのスクリーというわけである。
さて、いよいよお待ちかねのペンローズ図だ。
ミンコフスキー図をペンローズ図(図4左)にすると、tとrが、ψとξに変数変換されて、五つの無限遠点が、有限の距離にきたことがおわかりだろう(ψはギリシャ小文字のプサイ、ξはクサイ)。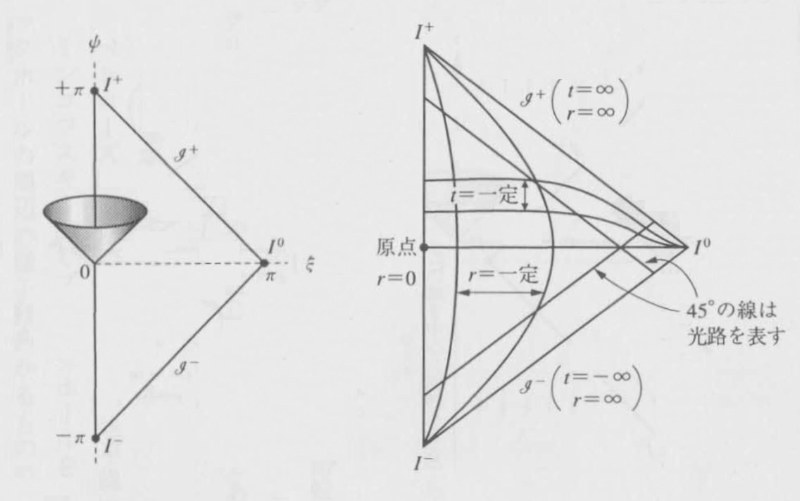
図4:ペンローズ図と拡大したペンローズ図
ここで、注目していただきたいのは、光の経路が、ミンコフスキー図と同じく、45度の角度のままな点だ。これは、角度を変えない変換という意味で「等角」変換と呼ばれている。ペンローズ図への変換は、光円錐をそのままに保つ特殊な変換なのである。
ミンコフスキー図に方眼をいれると、それがペンローズ図でどうなるかがわかる。時間tが一定の線と空間距離rが一定の線を確認してほしい。
これでわかることは、ペンローズ図というのは、ようするに、二つのスクリーを無限遠から有限のところまでググーツともってきてしまったものということだ。頭の中で想像してみてほしい(図4右)
つまり、光が進む方向を動かさないように固定して、光にとっての無限遠を有限の距離にもってきてしまったのである。ある意味で、全宇宙を小さな三角形の中にぐーっと縮めてしまったのである(正確には、三角形の縦軸を中心に回転させたもの。さらに言えば、そうやって回転させたとしても、空間の次元を一つ無視しているのだが)。
これは、ようするに、宇宙の無限に大きい時空図をぐぐーっと縮めて三角形の世界にして、全体像を俯瞰(ふかん)しているのだ。こうすると、宇宙のどこかで起こった事件が別の地点にどのような影響を及ぼすか、というような因果関係が明確になる。
ただ、ちょっと注意が必要だ。今、宇宙を三角形に縮めると言ったが、通常の時空図で四次元時空を二次元時空に簡略化して描いているのと同様、ここでも空間の三次元を一次元に簡略化してある。それがξ(クサイ)方向だ。空間を二次元にするには、ψ(プサイ)軸を中心にぐるっと一回転させてやればいい。
三角形を回転させると、円錐を二つくっつけたような形になる。アイスクリームコーンのコーンを二つ丸いところで接着したような形。宇宙を二つの合わせアイスクリームコーンの中に封じ込めたわけである。
ペンローズ図を使って、「事象の地平線」と「ホワイトホール」を考えてみよう。
ミンコフスキー図でブラックホールを眺めていても、あまりよくわからない。というか、ブラックホールの周辺の様子はわかるものの、遠くでどうなっているのか、中はどうなっているのか、あまりよく見えてこない。
そこで、ブラックホールをペンローズ図にすると、驚くべきことに、ブラックホールの大局的な構造が手にとるように見えてくる(図5)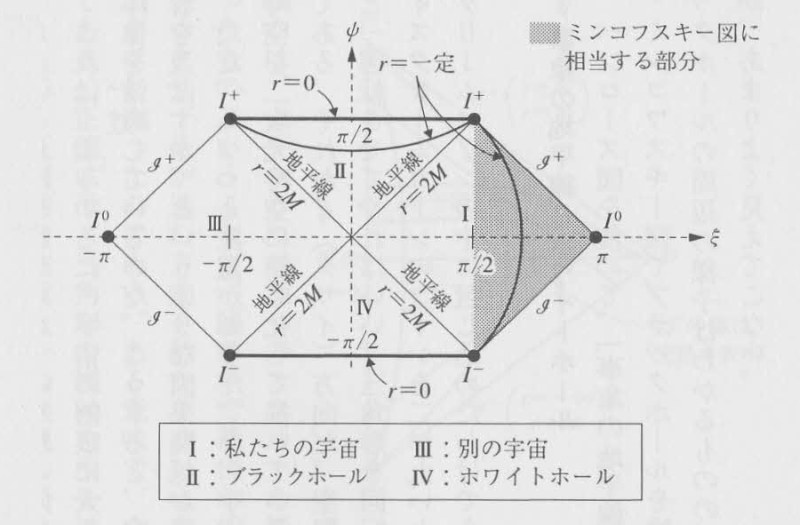
図5:ブラックホールのペンローズ図
この図の見方は少々難しい。
まず、一番右の漢数字Iと書いてある領域に注目していただきたい。これは、さっきやったばかりの三角形のペンローズ図を拡張した領域と考えてほしい。この部分は、ブラックホールの事象の地平線(r=2m)の外側である。
次に、r=2mという線を越えて領域Ⅱに入ると、そこはいわばブラックホールの中。もう外には出られない。
領域IとⅡは、それぞれ、領域Ⅰがブラックホールの外部で領域Ⅱが内部に相当するわけだ。原点からブラックホールに向けて光を発射すると、それは、シュヴァルツシルト半径(r=2m)を通って、ブラックホールの中に入って、やがて、特異点(r=0)に達する。
ここで、ブラックホールの内部Ⅱでは、tとrの役割が逆転していることに注目してほしい。領域Iでは、距離rが一定の線は上端から下端に伸びていたが、領域Ⅱでは、左端から右端に伸びている。
これは、物理的には、べつに時間と空間が逆転したわけではない。だが、領域Iでは時間が進むのを止められなかった人間は、領域Ⅱでは、特異点に向かって進むのを止められない。そう考えれば、ある意味で、空間と時間の役割が逆転したのだと思ってもらっても差し支えない。
特異点のr=0が、上下に二本ある線で表されているが、これは、無理やり無限遠点を有限のところまで引っ張ってきてしまったため、そのしわ寄せを喰って、特異点が間延びしたように見えるだけのこと。特に意味はない。
むしろ、問題は、領域ⅢとⅣの存在である。こりゃあ、いったい何だ?
実は、これがペンローズ図の威力なのだ。ペンローズ図は、無限の遠くまでも含めた全体像を見せてくれる。
領域Ⅳは、ブラックホールの時間を反転したもので、「ホワイトホール」と呼ばれている。ブラックホールの正反対の性格をもっていて、ホワイトホールからは、なんでも出ることはできるが、決して中に入ることはできない。
図の一番下の特異点を出発した光は、やがて、地平線を越えてホワイトホールの外に出てくる。領域Ⅳから領域Ⅲへは一方通行なのである。また、領域Ⅳから領域Iに出ることも可能だ。
だが、もし、われわれが領域Iに住んでいるとするならば、われわれは、決して領域Ⅲに行くことはできない。それは、われわれとは因果関係をもたない「別の宇宙」なのである。
今回は、長い文章になってしまいましたが、図も多く掲載しましたのでお許しください。「ペンローズ図」に少しは慣れたでしょうか。次回も出てきます。
今回は、CTL(閉じた時間の環)の話題に戻ります。それと平行してペンローズ・ダイアグラムを交えて書いていくことになります。
ゲーデルの宇宙の研究の延長として、CTL(閉じた時間の環)に関して、1974年に数理物理学者のフランク・ティプラーは、無限に長く質量の大きい円筒の表面が、光速の1/2以上の速度で回転すればCTL(閉じた時間の環)ができることを指摘しました。つまり、CTLに沿って円筒の周りを回転すれば、タイム・トラベルが可能であり、円筒の回転方向と同じ方向に回転すれば未来へ行き、逆方向に回転すれば過去へ行くことができるのです。
また、有限の長さの円筒の場合においても、ジョン・グリビンは、太陽と同じ質量で長さが100km、半径10kmの円筒を1ms(ミリ秒)に2回転させるとCTLができることを計算しました。天体の中には、パルサーといって数ミリ秒周期で電磁波を出しているものがあります。これは、非常に重い物体が超高速で回転しているということであり、宇宙の中にCTLが存在している可能性もあるのです。
有限の長さの円筒は、どんなに硬い物質で作ったとしても、半径方向は遠心力により支えられるますが、回転軸方向はその強力な重力によりつぶれてしまいます。つまり、ブラックホールになってしまうのです(下図参照)。
したがって、有限の長さの回転する円筒については、実現することはできません。
ブラックホールによるタイム・トラベルを理解するには、ペンローズ・ダイアグラムを理解する必要があ理ます。この宇宙を表す地図には、球面を二次元で表現するために様々な図法が用いられています。ペンローズ・ダイアグラムは、時空間を二次元で表現する図法の一つです。そして、通常の時空間のペンローズ・ダイアグラムを下左図のように示します。左図の点Pは時間的過去の無限大、点Fは時間的未来の無限大、点Eは空間的無限大、辺Sは光的過去の無限大、辺Dは光的未来の無限大を示します。
光的過去の無限大Sとは、光速で進む信号で知ることができる最大の時空間を現しています。そして、辺Sから発射された光は、左上方45°の傾きで現地点の時間線に到達します。辺Sより遠方または過去の世界は知ることができません。光的未来の無限大とは、光速で進む信号を送ることができる最大の時空間を現しています。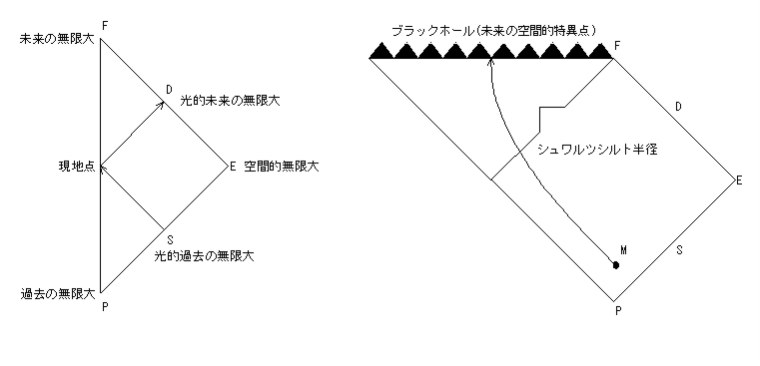
まず、シュワルツシルト・ブラックホールをペンローズ・ダイアグラムで表してみましょう。すると少し複雑な上右図のような形に表されます。
時空のゆがみが無限大となる特異点が生じます(ペンローズ・ダイアグラムでは、慣例として特異点をギザギザの線で表す)。特異点からシュワルツシルト半径だけ離れたところに、一方通行の膜(線分EPと平行な点Fからの直線を折った膜)があります。点Mから出発した旅行者は、一方通行の膜を通りぬけて特異点に吸い込まれ、そこから出ることはできません。
それでは、アインシュタイン方程式のシュワルツシルトの解のすべてをペンローズ・ダイアグラムで表現すると下図のようになっています。この図から、一方通行の膜をもつ第二の宇宙が出現していることがわかります。さらに、物質を吐き出すホワイトホール(過去の空間的特異点)が発生しています。ホワイトホールは、ブラックホールを時間反転したものといえます。ホワイトホールのシュワルツシルト半径も一方通行の膜なのですが、この膜は物質を吐き出すだけで内部に入れることはありません。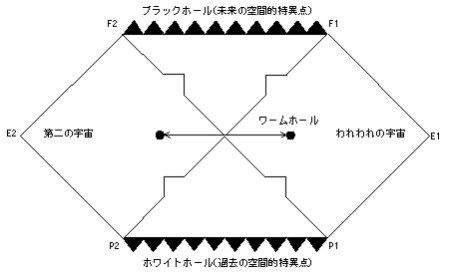
現在までに、この宇宙の中で、ブラックホールと考えられる天体は、いくつか発見されていますが、ホワイトホールと思われる天体は未だに発見されていません。
この宇宙の中には、ホワイトホールは存在しないのかもしれないか、あるいはいままでと違った解釈をする必要があるのかも知れません。
アインシュタイン方程式の解で出現する第二の宇宙は、前回書きましたように1935年に、アインシュタインとナザン・ローゼンが、素粒子のモデルとしてシュワルツシルトの解を使おうとしたときに発見されました。
第二の宇宙は、われわれの宇宙とは独立した別の宇宙だあるかもしれないし、われわれの宇宙の離れた領域かもしれません。アインシュタインとローゼンは、第二の宇宙は、われわれの宇宙の離れた領域と推定しています。
二つの宇宙は、光より速い信号を使わないと通信できないようです。二つの宇宙をつなぐ超光速の空間的結びつきを、「アインシュタイン=ローゼン・ブリッジ」または「ワームホール」と呼ぶということはすでに書きました。
話は少し飛びますが、量子力学の世界では、「量子テレポーテーション」という瞬時に量子の状態が伝わる現象があります。これは、ワームホールによる現象ではないかと考えられています。
何もない空間にガンマ線を照射すると、電子と陽電子が対生成することは実験で確かめられています。
電子と陽電子は、互いに逆向きのスピンを持っていますが、不確定性原理により、スピンの向きは観測するまで不確定です。対生成した片方の電子のスピンの状態を観測してアップスピンだったとすると、その瞬間にもう一方の陽電子のスピンの向きがダウンスピンに確定するのです。電子と陽電子がどんなに離れていたとしても瞬時に確定するのです。このような対の量子の状態を「量子もつれ」といいます。
量子テレポーテーションは、実際に粒子が別の空間へ移動することではなく、量子もつれの状態の片方の量子の状態が確定すると、瞬時にもう一方の量子の状態も確定することをいいます。
シュワルツシルトのブラックホールは、第二の宇宙が出現するため、大変興味深いのですが、この第二の宇宙と通信するには、超光速信号を使わなければなりません。量子テレポーテーションは、量子の状態が瞬時に確定するというだけで、情報を超光速で送れるわけではないようです。
たとえ、ワームホールを使って第二の宇宙に行くことができたとしてもタイムトラベルは不可能であるようです。
シュワルツシルトがアインシュタイン方程式の解を発表したのとほぼ同じころ、ドイツの物理学者ハインリッヒ・ライスナーとフィンランドの物理学者グンナー・ノルドストロームは、質量だけでなく電荷も持っている場合のアインシュタイン方程式を解きました。ライスナー=ノルドストロームのブラックホール・ダイアグラムは下図のようになります。
これには、二つの大きな特徴があります。それは、時間的特異点とペーパードール・トポロジーです(折りたたんだ紙から切りぬいた紙人形のようなので、ペーパードール・トポロジーといいます)。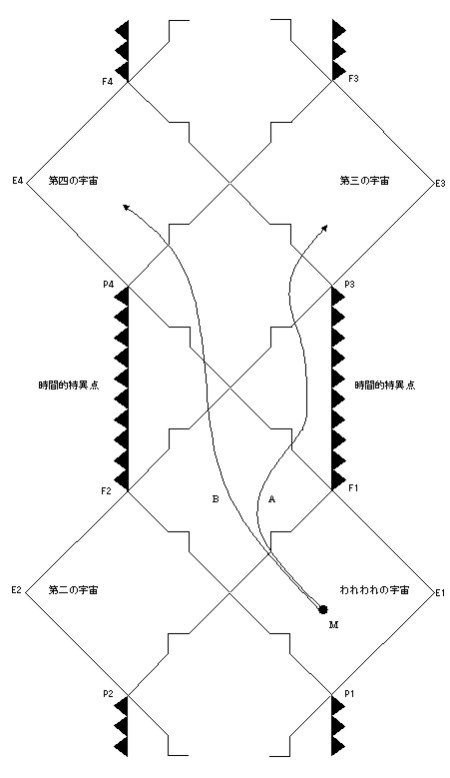
シュワルツシルトのブラックホールの中心には空間的特異点が存在しました。これに対して、ライスナー=ノルドストロームのブラックホールには時間的特異点が存在するのです。
また、通常空間と特異点を隔てる一方通行の膜が二つ存在します。時間的特異点は、時間の流れに並行しており、空間的特異点と違って、時空を巧妙に航行すれば避けることができるのです。
たとえば、Mから出発した旅行者は通路Aを通って、時間的特異点を避けて第三宇宙に到達できます。また、通路Bを通って第四宇宙にも到達することもできるのです。
一方通行の膜は、通過すると時間が空間に変わり、空間が時間に変わります。一方通行の膜を奇数回通過すると空間的特異点に到達し、偶数回通過すると時間的特異点に到達するのです。
時間的特異点は、入口用と出口用の二つの一方通行の膜を持っていて、ブラックホールとホワイトホールの両方の働きをします。そして、シュワルツシルトのブラックホールには別の宇宙が一つあるのに対して、ライスナー=ノルドストロームのブラックホールには別の宇宙が無数に現れます。
別の宇宙は、まったく別の宇宙かもしれないし、われわれの宇宙の一部かもしれない。また、元は一つの宇宙だったものが分裂して、ほとんど同じような歴史をたどっているパラレル・ワールドなのかもしれない。時間旅行者が過去に戻った時点で宇宙が分裂し、われわれの宇宙とそっくりのパラレル・ワールドが形成されるのかもしれない。
もしそうだとしたら、自分が過去に戻って親を殺したとしても、そこは自分のいた世界とは別の世界なので、自分が消滅することはない。すなわち、親殺しのパラドックスは生じないのです。
ライスナー=ノルドストロームのブラックホールが発生した時点で、われわれの宇宙から分裂したパラレル・ワールドが出現するとしたら、時間旅行者が別の宇宙に到達した時点では、われわれの宇宙とまったく同じような世界になっていて、その時点から少しずつ未来が変わっていくと考えられます。
時間旅行者は、一方通行の膜があるので、元自分が住んでいた未来に戻ることはできません。ただし、ほとんど同じような未来の世界に戻ることはできるかもしれません。
しかし、ライスナー=ノルドストロームのブラックホールは、強力な重力に抵抗するだけの強力な電荷が必要です。そのような強力な電荷は、そこにあるどんな物質もイオン化し、そのイオンによってブラックホールの電荷を中和するように働くので、宇宙の中にはライスナー=ノルドストロームのブラックホールは存在しないと考えられています。
別の宇宙がわれわれの宇宙の離れた領域とすると閉じた時間の環CTLが形成され、タイムトラベルは可能ですが、そうでない場合は、ライスナー=ノルドストロームのブラックホールではタイムトラベルは不可能です。
2006年に、タイムマシンの特許が公開されました。
タイムマシンの特許は、オクラホマのマービン・B・ Pohlman 博士によって合衆国特許商標局に出願されています。
特許の全文は下記からダウンロードできます。
http://www.google.com/patents?id=oH2bAAAAEBAJ&zoom=4&pg=PA1#v=onepage&q&f=false
この特許の中の図面が、2000年11月にインターネット上で、2036年からやってきたと自称しているジョン・タイターが公開した、タイムマシン操作マニュアルの中にある図面と全く同じです。特許の中には、PDFファイルをご覧になるとわりますが、数式が書かれており特許というより物理の小冊子のような感じです。
もしかすると、ジョン・タイターとは、マービン・B・ Pohlman 博士だったのではないでしょうか。
それでは、タイムトラベルについてですが、タイムトラベルには、必ずこれに伴うタイムマシンという機械を考慮に入れる必要があります。タイムマシンは機械ですから、それを製造する技術も必要になってきます。
ですから、このブログではタイムトラベルに関係する物理的な問題が中心となった記述になってしまいます。
タイムトラベルにとって、最も大事な要素としては「時間」と「空間」の関係は必然です。そのため、どうしてもアインシュタインの相対論と最先端の宇宙論を中心に考えていかざる得ません。
そこで、今回はブラックホール・ホワイトホール、そしてこの二つをつなぐ橋であるワームホールに関係する話、「アインシュタイン・ローゼン橋」から書き進んでいきます。
1917年、アインシュタインは一般相対性理論の方程式を完成し、重力により時空がゆがめられることを説明しました。そして、その同じ年に、ドイツの天文学者カール・シュワルツシルトが、球対称で回転していない質量の周りの、ゆがんだ時空を記述するアインシュタイン方程式の解を発表したのです。
シュワルツシルト半径より内側からは光でさえ飛び出すことができません。もし太陽と同じ質量の天体が収縮したと仮定するとシュワルツシルト半径は約3kmになります。このシュワルツシルト半径より更に凝縮した天体はブラックホールになってしまいます。
アインシュタインは、もともと、ブラックホールは自然界に存在しないだろうと考えていました。しかし、そんな思いとは裏腹に、その後、ブラックホールがだれも考えつかないほど奇妙で、中心にワームホールが存在する可能性すらあることを明らかになってきました。
数学者はこれを多重連結空間と呼ぶ。物理学者がワームホールと言うのは、地中の虫(ワーム)が地中を掘り進むようにして、二点間を結ぶ穴(ホール)を作るものだからです。このワームホールは、次元の入口と呼ばれることもあります。呼び名はどうあれ、これはいつの日か次元間旅行の究極の手段となるかもしれないのです。
ワームホールを一般に示した最初の人物は、ルイス・キャロルというペンネームで本を書いたチャールズ・ドジソンです。『鏡の国のアリス』のなかで彼は、鏡という形でワームホールを持ち込んだのです。その鏡を介して、オックスフォードの田舎と不思議の国がつながっていたのでした。
オックスフォード大学の数学講師だったドジソンは、多重連結空間のことをすでに知っていました。多重連結空間は、定義上、輪を縮めても一点にできないような空間のことです。通常は、どんな輪もたやすくつぶして点にできます。しかし、ドーナツのような形の空間を考えた場合(これが多重連結空間)、その表面にドーナツの穴を取り囲むように輪を置けるのですが、この輪を空間のなかでつぶしていっても点にはできません。穴の輪郭までしか縮められないのです。
1935年、アインシュタインと教え子のネイサン・ローゼンが、ワームホールを物理学の世界に持ち込みました。
アインシュタインとローゼンは、電子(一般に何の構造ももたない微小な点と考えられている)をブラックホールと見なす斬新なアイデアを思いついたのです。このようにすれば、一般相対性理論は、統一場理論における量子の世界の謎を説明するのに利用できるはずです。
ふたりはまず、長い首をもつ大きな花瓶にも似た、一般的なブラックホールの解に注目しました。そして首(ブラックホールでは喉と呼ばれる)の部分を切り、別のブラックホールを逆さまにしてそれにつなげたのです。アインシュタインの見たところ、この奇妙だが滑らかにつながった形状によって、ブラックホールは中心に特異点がなくなり、電子のように振る舞う可能性がありました。
電子をブラックホールと見なすというアインシュタインのアイデアは、失敗に終わりましたが、今でも、宇宙論者達は、アインシュタイン・ローゼン橋がふたつの宇宙をつなぐ通路になりうると考えています。宇宙を飛びまわっていて、たまたまブラックホールへ落ちてしまうと、一気に穴へ吸い込まれて(ホワイトホールから)向こう側へ出る可能性があるのです。
アインシュタインにとって、自分の方程式の解が物理的に妥当な前提から出たものなら、物理的に存在可能な物体に対応するはずでした。しかし彼は、だれかがブラックホールに落ち込んで並行宇宙に出るということは考えもしなかったようです。
ブラックホールの中心では潮汐力が無限大になるので、不幸にもそこへ落ちた人間は重力場で原子までばらばらになってしまうからです。
(アインシュタイン・ローゼン橋は一瞬だけ開くが、すぐに閉まるため、どんな物体もそこを抜けて向こう側に到達することはできない)。
要するにアインシュタインは、ワームホールが存在するとしても、生きて通り抜け、それを報告できるような生物はいないとする態度をとっていたのです。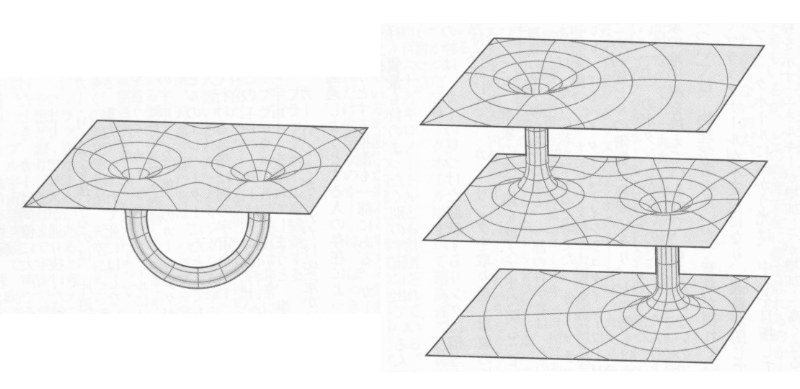
アインシュタイン・ローゼン橋; ブラックホールの中心には、われわれの宇宙にある別の場所や、別の宇宙の場所と,時空をつないでいる「首」がある、静止したブラックホールを通ると命はないが、回転するブラックホールなら、リング状の特異点をもつので、そのリングを通ってアインシュタイン・ローゼン橋を抜けられるかもしれない。ただし、これはまだ推測の域を出ていない。
光の速度は、発光体が止まっていても動いていても、観測者が止まっていても動いていても一定です。下左図は光円錐を示しています。XY軸が距離、Z軸が時間で、原点が現在の位置、時間を示しています。光の速度で進んだ場合に光円錐上を未来へ進んでいきます。光速を超えることはできないので、光円錐の外側に行くことはできません。つまり、光円錐の内側は、私たちが知ることができる世界を現しています。
1949年、数理論理学者クルト・ゲーテルは、アインシュタイン方程式のひとつに更に奇妙な解を発見しました。彼は全宇宙が回転していると仮定すると、宇宙の中の人は糖蜜のような性質を持つ時空に引きずられることになります。このゲーデルの宇宙を一周すると、初めの場所に戻ってきた時に時間を遡っているのです(下右図参照)。
ゲーデルの宇宙では理論上、宇宙の中で時間的・空間的にどの二点間であろうと移動できます。どんなに遠い過去の出来事も見に行けるのです。一方、ゲーデルの宇宙には内向きにつぶそうとする重力が働いているため、回転の遠心力はこの重力と釣り合っていないとまずいことになります。つまり、この宇宙はある程度以上のスピードで回転している必要があるのです。宇宙が大きければ大きいほど、つぶそうとする重力も大きくなるので、つぶれないように早く回転しなければなりません。
下の右図を見てください。この図で、宇宙の重力と宇宙の自転による遠心力が釣り合う回転の半径を臨界値Rとすると、臨界値Rを超えたところでは、時空のねじれによって、未来の光円錐が近くにある過去の光円錐と交差しています。リングを一周すると、自分の過去の光円錐へ戻ってくることができます。このような閉じた時間の環をCTL(Closed Time Link)と呼びます。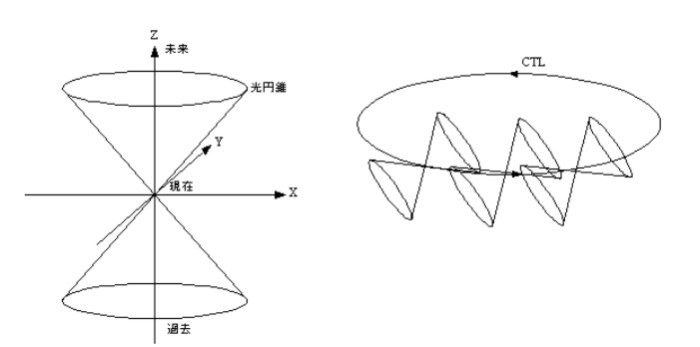
図左;光円錐 図右;CTL
われわれの宇宙に当てはめて計算すると、700億年で1周する速度で自転していなければならなりません。そのときの臨界半径はおよそ160億光年で、CTLの長さは約1000億光年となります。非常に長い距離になるのですが、光速に近い速度の宇宙船で旅行すれば、ウラシマ効果によって内部の人間にとっては1年程度で旅行することができます。しかし、光速に近い速度まで加速するためには、膨大なエネルギーが必要なため、現実的には不可能でしょう。
もし、宇宙が自転しているとすると、ビッグバンの残留放射線(宇宙背景輻射)に非等方性が生じているはずです。しかし、観測された結果によると、残留放射線の等方性が高いことから、宇宙はほとんど自転していないと考えられています。したがって、この方法ではタイムトラベルすることはできません。
アインシュタインは、プリンストン高等研究所の同僚である友人が見つけた解に、大いに困惑しました。彼の反応にそれがよく表れています。アインシュタインの反応は、ふたつの理由で関心をそそられたようです。
第一に、彼が、一般相対性理論を打ち立てたときにタイムトラベルの可能性に悩まされたことを認めています。時間と空間はぐにゃぐにゃに曲げられるゴムのように扱えるので、時空の生地を十分に曲げるとタイムトラベルができてしまうのではないかと案じたのです。
そして第二に、アインシュタインは、「物理学的な理由」--つまり、宇宙が回転しておらず、膨張しているという事実--をもとにゲーデルの解を排除しました。
アインシュタインが亡くなったころには、彼の方程式が、タイムトラベルやワームホールといった、奇妙な現象を可能にしてしまうことは広く知られていました。しかし、自然界では実現できないと思われていたため、その可能性をまともに考慮する人はいなかったのです。
そのような解は現実世界とは関係がなく、ブラックホールを通って並行宇宙へ行こうとしても死んでしまうはずです。宇宙は回転しておらず、無限に長い筒は作れないのでタイムトラベルはあくまでも理論上の問題だ、とだれもが考えていたのでした。
ところが1963年、この見方に変化が生じます。ニュージーランドの数学者ロイ・カーが、アインシュタインの方程式に、最も現実味のありそうな星の死に方を表す厳密解を見つけたのです。
それが、回転するブラックホールでした。角運動量保存則により、星は重力でつぶれるにしたがい、自転する速度を上げます(フィギュアスケートの選手が回転する時、腕を縮めると速く回るようになったりする)。
自転する星は、つぶれると中性子のリングになり、強烈な外向きの遠心力が内向きの重力を打ち消すのでそのまま安定します。そうしたブラックホールは、驚くべき性質をもっています。
このカー・ブラックホールに落ち込んでも、あなたはつぶれて死にはしないでしょう。アインシュタイン・ローゼン橋を通ってどこかの並行宇宙に出られそうなのです。
「この魔法のリングを抜けると、あら不思議、君は半径も質量も負のまったく別の宇宙に出ているんだ!」
この解を見つけたとき、カーは同僚に大声でそう言ったそうです。
つまり、アリスが通り抜けた鏡の枠は、カーの見つけた回転するリングに相当します。しかし、このカー・リングを抜けるのは、片道切符の旅になるのです。
カー・リングを取り巻く事象の地平線を通過するとき、重力でつぶれて死にはしないにしても、事象の地平線を越えてまた戻ることはできないのです(実を言うと、カー・ブラックホールには事象の地平線が二つある。一部の科学者は、その並行宇宙とわれわれの宇宙をつなぐ第二のカー・リングがあれば、帰りの旅ができると考えた)。
前回で、時間について書きましたが、この「時間」とは、「質」と「量」を別の要因として考えなければならないものなのです。しかし、現代科学では「物質」として決められたものとして扱ってきました。そのため、一定の定数が生まれてしまったのです。それが「光速」であり、「プランク定数」というものを創り出してしまいました。結果として「光速」は「一定不変」であると見なしてしまい、この「光速」のために皮肉にも「時間」を拘束してしまったのです。
我々の現代科学は、最初に「光速不変」は当然の帰結であるとして、物理学の法則を構築していったのです。そして、このことを柱として、マクロは宇宙論へ、ミクロは素粒子の探求へと突き進んで行かざる得ませんでした。
このように、現代物理学での宇宙論では、最初に「ビッグバン」で「光速」の光が放たれて、宇宙はスタートし、そしてこのビッグバンは「特異点」の「量子的ゆらぎ」として突然に発生してしまったかのようにされてしまいました。
この宇宙論に関しては、ここのブログでも「宇宙」という項目の中でおおく取り上げてきましたので、そちらの方を参照してください。
これと同じことが、素粒子の世界でも行われていて、原子は原子核と電子により構成されており、この原子核は中性子と陽子から、そしてこの中性子と陽子、それと電子はともにクオークから構成されていることになっています。つまり、クオークを始原素粒子にすることで統一しようとしました。
しかし、ここまでに述べてきた素粒子は、スピン1/2の素粒子であり、スピンが1や2の「光子や重力子」とは性質が「スピン」を中心として考えた場合、統一は不可能です。そこで、今度は大統一理論や究極理論として「スピン」も含めた、すべての素粒子を統一しようと、多くの一線級の物理学者がこの問題に取り組んでいます。
この、究極理論には超ひも理論・超重力理論や最近ではブレーン理論などが有力候補に挙がっています。しかし、これらの理論には常に付きまとっているものが存在しています。それが、「特異点」といわれている「プランク定数」なのです。
では、この宇宙論と素粒子論について、共通点を探してみることにします。するとどちらにも「スピン」という回転運動が含まれてくることに気づくはずです。
「UFOと超科学」その3、にて「円輪波」について書いてありました。そこには、 この「円輪波」の持つエネルギーに相応した「一(いち)」の核を中心、「一」の単位として、無限の波動運動を持続しながら、一大中心に統御されているのは電子も星も同じです。この「円輪波」はちょうど浜辺に押し寄せる波の如く、陰陽・高低となり渦状となって、大宇宙の中に流れ込んでいるのであります。この状態を「波動帯」と申し上げたのですが、帯(おび)と表現したその意味をよく理解していただきたいのです。
ここに書いてあるように、銀河系の中心(一)に太陽系が回転し、その太陽の中心(一)の周りに惑星が回転しているのです。この現象を外の世界から眺めてみると、銀河系を中心に太陽系が渦を巻いた帯のように回っているのが見えるはずです。同様に太陽系と各惑星についても同じことがいえます。
マクロにあることはミクロに同様に神写しされるはずですから、この宇宙が「同一物質」で出来ていることを大前提として考えてしまうと、私たちが空間を3次元の世界であると認識している、この宇宙空間は、すべて「光速不変」の世界へと変わってしまうことでしょう。
この考え方こそが、我々の認識している「空間」と言うことになってしまいます。しかし、本当にこれで良いのでしょうか。宇宙人は「空間」をどのように捉えていたのでしょうか。以下に示します。
空なる十字交差の一点を基準として、「内」に現われたのがその星の「時間」です。「外」に現われたのがその星の「空間」です。大宇宙の中心は「時空一つ」に溶け合って輝きます。それまでの段階として、星々の時空は皆一つとして同じものはありません。縦横十字に交差した「ところ」が「空(くう)」、「空」なる「ところ」がその星の科学の出発点となります。
それでは、《「内」に現われたのがその星の「時間」》とはどういうことなのでしょうか?
ここで私たちは、「時間」という概念を熟慮する必要が出てきました。現在は時間の基準を原子(クオーツ時計など)の振動数から決定していますが、少し前までは太陽暦によって1年365日として歴を創り、それを基準として時間を決めていました。
しかし、ここで取り上げている宇宙人の時間の概念とは掛け離れているように思われます。なぜなら、「時間」とは人間が「今」を認識し、そして次の「今」を次々と積み重ねることで出来上がってくるものです。そうすると、人それぞれが別の「今」という「時間」を積み重ねているのと同等なことに気づかされます。つまり、人はそれぞれの時間を自分で創っているために、その「1人の人」は自分を基準にとると、他の「すべての人」とは時間を異にしていることが解るはずです。
この「時間」に対する考え方を、人類が獲得した暁には、現代の科学文明そのものの固定観念が崩れ去っていくことでしょう。
最後に、今回は時期尚早のため「次元」についての考察は次回以降に回したいと思っています。
ここまで、読んで下さって、本当に有り難うございました。
ハンネス・アルベーン (Hannes Olof Alfvén)
この物理学者の名前をご存じでしょうか。
1963年にオックスフォード大学よりCosmical Electrodynamics(宇宙電気力学)として
出版された書籍の著者です。
昭和55年に、日本語翻訳本が講談社より、「宇宙電気力学--その基礎原理--」という書名で出版されています。
今まで、3回にわたって「UFOと超科学」をここのブログにアップしています。
私は、昭和50年に村田正雄氏の本を読んで感銘を受け、前回の最後に書いておりましたように「波動帯」「直射する波動」「円輪波」という言葉が何時までも忘れられずに、数年が過ぎ去ってしまいました。
なぜなら、その当時の物理学の世界では、絶対的な真理としての量子論、そして相対性理論がもてはやされていた時期です。
しかし、当時の時空概念ではこの太陽系を行き来するだけでも、ぼう大な年月が掛かってしまい、到底、宇宙空間を自由に往来するような「空飛ぶ円盤(UFO)」の動作方法などの発想はとうてい説明することなど出来ませんでした。
このようなことを考えていた時に、本屋さんで偶然アルベーンの書籍に出会いました。私は物理の勉強を初めて、あまり経っていませんでしたので、この本の内容は難解すぎて正直あまり分かりませんでした。しかし、UFOの飛行原理を説明するにはこれしかないという思いだけは消し去ることが出来ませんでした。
アルベーンの宇宙プラズマに関する研究は、電磁気流体力学(MHD)の分野の開発につながりました。電磁気流体として数学的にプラズマをモデル化する。そして、1970年にノーベル物理学賞を獲得した業績の分野がMHDでした。
その後、宇宙電気力学は多くの宇宙の現象を記述するために、天体物理学者と天文学者によって使われています。しかし、アルベーンは、プラズマの多くの特徴が宇宙プラズマでより重要な役割を演ずることと感じていたのでしょう。
今では、宇宙電気力学という言葉はあまり使わず、プラズマ宇宙論ということばで表現されています。
では、プラズマ宇宙論とは、どのような学問なのでしょうか。Wikipediaを参考に書いていきます。
プラズマ宇宙論とは、宇宙論の一種で、宇宙的スケールの現象は重力だけではなく、宇宙の物質の99.9%を占める電気伝導性の気体プラズマの運動に起因する、巨大な電流と強力な磁場の影響を大きく受けているとする。そして電磁気力と重力の相互作用によって、壮大な現象を説明できると主張する。
プラズマ宇宙論は、ビッグバン理論と比較して、銀河の回転曲線問題を暗黒物質という仮定の物質を持ち出すことなく簡潔に説明できる。さらに、近年発見されたヘルクレス座・かんむり座グレートウォール、U1.27といった宇宙構造体の成り立ちを説明する際、現行のビックバン宇宙論(から発展した理論も含む)では存在自体が矛盾してしまう程巨大な宇宙の大規模構造も、プラズマ宇宙論では矛盾無く説明できる。
しかしながら、プラズマ宇宙論は宇宙マイクロ波背景放射の観測事実をうまく説明できていない。そのため、プラズマ宇宙論は現時点では標準的な理論とみなされていない。
最近の宇宙の観測結果等の研究から、銀河は大規模構造体を形成している事がわかった。その大規模構造は、銀河団の巨大な壁「グレートウォール」と銀河がほとんど存在しない超空洞「ボイド」とが複雑に入り組んだ構造である。その形はプラズマ現象でよく見られるフィラメント構造をしている事が分かっている。
非常に複雑な形態を見せる惑星状星雲は太陽程度の質量を持つ恒星の最期の姿である。このことは、複雑な形態は重力ではなく磁場が大きな役割を果たしていることを示している。そして、この惑星状星雲もプラズマで形成されており、そこには特徴的なフィラメント構造が多く見られる。これはプラズマの自己組織化によって生み出される形であり、その内部にはビルケランド電流と呼ばれる電流が流れている。
われわれを照らし出す太陽も同様に巨大なプラズマの塊である。太陽から放出される高速のプラズマは惑星空間を通り抜けて地球に達し、オーロラ、北極光、磁気嵐、電波障害などを引き起こす。一般に真空と言われる宇宙空間だが、このようなプラズマに満ち、プラズマ・ダイナミクスが支配する空間であり、常に休みなく変化を見せている。
惑星、太陽系、銀河系、星間ガス、星雲、銀河団、彗星などなど、宇宙にあるすべての物質はプラズマの影響を受けている。その豊富にあるプラズマが宇宙の広い範囲にわたって重要な役割を果たしている。
アルベーンは次のように述べている。
「宇宙についての理論は、われわれが観測や実験で確かめた事実の延長上に打ち立てられなければならない。われわれは(ビッグバン理論のように、最初に宇宙誕生の姿を想像して、そこから現在の宇宙に進化するまでを推測して理論にするのではなく)、まず今の宇宙の姿を調べ、それを元にしてより遠い過去へ、より不明瞭な時代へと遡っていくべきである」
これは、プラズマ宇宙論の基本的な考え方はビッグバン理論とは対極であるといえる。プラズマ宇宙論は、厳密な意味で定常宇宙論とは大きく異なる。プラズマの特性上それは必然と言える。つまりプラズマは一つの場所にとどまるということはしない。常に反発や引き合い、衝突などを繰り返し変化し続けている。それが積み重なり大きなスケールの変化が起き始め大規模な構造を作り出すと考えられている。その大規模構造はビッグバン理論が重視する重力ではなくプラズマの中を流れる電気と、それがつくりだす磁場によって形成される。このことは、現在ビッグバン宇宙論では説明の難しい「グレートウォール」などの大規模構造を解明する糸口になる可能性がある。
プラズマの長さが1万光年から10万光年にも達するほど集まった場合、その中を巨大な電気が流れ出し、それが非常に大きな磁場を発生させる。次に電気と磁場の相互作用によってプラズマの形はさまざまな変化を見せる。隣接したプラズマのガスの柱どうしは引き付け合い、絡み合うことにより複雑な構造を作り出す。
現在、プラズマ宇宙論は非主流派の理論である。しかし、成熟した体系である電磁流体力学 (MHD)を基盤とし、ともに発展してきたこの理論は非常に多くの成果を収めている。太陽のプロミネンス、渦巻銀河、宇宙の大規模構造に至るまで、他にも様々なスケールの問題に関して説明をしている。これからの観測技術の向上に伴い、今後の発展が期待される分野であると言える。
銀河形成のシミュレーションに成功し、天文学最大の謎、銀河の回転曲線問題も解決。
ロスアラモス国立研究所の物理学者であった、アンソニー・ペラットは、パルス発電機でX線放射の実験を行っていた。発生したプラズマ・フィラメントはお互いの磁場で引き寄せられ、集合したプラズマは合体して螺旋を形成し、螺旋は強力なX線を放ち、銀河の螺旋構造と同じだったのである。この絡み合うフィラメントの中を流れる電流は、ビルケランド電流と呼ばれ、プラズマ宇宙論では重要な役割を果たす。
かつてプラズマ宇宙論の創始者ハンネス・アルベーンの下で研究していたペラットは、この螺旋が銀河の渦巻構造を解明する手がかりとなると考えるにいたった。彼は当時最先端のプラズマ・シミュレーション・プログラム「SPLASH」を使い、プラズマの動態をシミュレーションし、多くの特徴的な銀河の渦巻が、完全に磁場の中を漂うプラズマ・フィラメントで再現できる事を発見した。
これによって銀河における大きな謎であった銀河の回転曲線問題まで、解明する事ができた。
この問題は銀河が重力によって支配されていると仮定すると、中心から外側に行くにつれて渦巻きの腕の速度が遅くなるはずである。しかし実際は外側も同じ一定の速度なのである。この矛盾を解決するために多くの研究者達は苦慮し天文学の大きな謎の1つとされ、見えない物質である暗黒物質が銀河を取り囲んでいると仮定し、この問題を解こうとしてきた。
ペラットとジム・グリーンは、シミュレーションを繰り返すことによって暗黒物質を仮定せずにこの問題を解決したのである。
プラズマによって支配されている銀河の渦巻きの腕は、例えると中心から伸びたバネのようなものである。このようなバネは全長にわたって同じ回転速度をもつことになる。それによってプラズマの圧縮が一定の曲線を作り出すことを示し回転曲線問題を磁場によって解決したのである。
そのとき、曲線にうねりが見られたが、実際にそれは渦巻きの腕が回る際に行なうローリング運動として観測と一致したのである。
これらの実験室で作られたミニチュア銀河はプラズマの特性の一つであるスケーラビリティーによって実験室レベルから太陽、銀河そして宇宙論レベルまで時間軸などの変数をかえるだけで広げる事が出来るのである。
宇宙構造体の成り立ち
現在、銀河、銀河団、超銀河団などの宇宙構造体の形成に関して次の2つの説が考えられている。
1:銀河が最初に生まれ、それらの重力が銀河群や銀河団を形成させる。そしてその集合体が、さらに集まり超銀河団や宇宙の大規模構造ができたという説、
ボトムアップ説:銀河系→銀河団→超銀河団→宇宙の大規模構造
2:大規模構造となる巨大なガスのかたまりが最初に生まれ、その次に超銀河団のもととなる塊が分裂する。そして徐々に銀河団から銀河群が分かれ、それが分裂し銀河になる。つまりスケールダウンしていき順に小さい構造が形成されたという説、
トップダウン説:宇宙の大規模構造→超銀河団→銀河団→銀河。
プラズマ宇宙論では、2番目のトップダウン説によって宇宙の構造体の起源を説明している。
プラズマは一般に揺らぎに対して不安定であり、最初の揺らぎは微小なフィラメントもしくは、渦の形成である。これらの渦は、同じ方向に動いているほかの渦を引き寄せながら、成長していく。
膨大な時間をかけて、プラズマは、より大きなフィラメント的な渦を発達させていく。エネルギーの流れは次第に大きくなって行くが、フィラメントの成長は、ほぼ1000キロメートルの特性速度によって限界付けられている。渦が大きくなるにつれて、成長速度は低下していく。渦の成長と電流の大部分を運んでいた陽子のシンクロトン放射によりエネルギーの損失は均衡し渦は成長を止める。
そのとき最大のフィラメントは直径100億光年に成長している。大きなエネルギーの流れが平衡から遠ざかるにつれて、重力的不安定性が生じる。フィラメントの、わずかな重力的収縮がその重力を増大させ、さらなる収縮を促す。このような収縮は新たなフィラメントのシステムを誘導し、収縮する物体の中心に向かって電流を引き寄せる。
収縮によって生じた重力的エネルギーは部分的に電気的エネルギーに転換される。磁気のエネルギーは収縮する他の天体のプラズマと相互作用する事により、新たなフィラメント・システムを生み出し、それが増大する角運動量を分布させ、プラズマを圧縮し、より大きな重力エネルギーの解放を可能にする。
ここで、不安定性の新たなサイクルが生まれた事になる。宇宙は巨大な送電網になり重力エネルギーを電気に転換する。それが、動力を供給し、より多くの物質を圧縮して、より多くのエネルギーを解放する。
この新しい揺らぎのサイクルは、宇宙大規模構造、超銀河団、銀河団、銀河、星、などの階層を作り出す。
収縮の各段階には固有の自然な限界がある。軌道速度がある幅の中に収まるような集中した天体を生みだす。それぞれの天体は順に部分に分裂する。その1つ1つは固有のフィラメント電流を持ち、それ自身の子孫を生む。
重力エネルギー解放の1つのサイクルの「廃棄物」が、次のサイクルの「原料」になっているのである。
ここまで読み進めてくると、在ることに気づく人が顕れてくることでしょう。
このブログで、プラズマ宇宙論を取り上げた理由は、前回まで書き進めてきた「UFOと超科学」の中で、宇宙人と称された方々が説明されていました、「波動や振動」に関しての昭和50年当時の科学者にも理解出来そうな内容です。人類の皆さんにも解って戴きたいという思いを多くのひとに伝えたかったのでしょう。
今回のテーマは「超科学のための補足」としました。









