パウリが「一三七」に「はまって」しまっていたとは思えない。それでも彼は一九三四年にハイゼンベルクに送った手紙のなかで、鍵となる問題は「一三七と電荷の『原子的神秘性』をうまく処理すること」だと書いている。当時パウリは、電子の質量と電荷が無限大になってしまうことのない量子電磁力学の形式を見いだそうとしていた。だが式をどう操作しても、必ず電荷の概念が入り込んでしまう。だからパウリは、「電荷の原子的神秘性」--「原子」という言葉と「神秘的な」という言葉を合わせたもの--と言ったのである。
問題はこういうことだった。つまり、量子電磁力学の理論には微細構造定数αを構成する要素として電荷が入り込んでくるのに、量子電磁力学の理論は「電荷の原子論的性質を考慮に入れていない」のである。将来の理論は「基礎となっている考え方を、その根底において統合しなければならない」とパウリは書いている。
パウリの考えでは、問題の核心は電荷という概念が古典物理学、量子物理学のどちらにとっても異質のものであるという点にあった。古典物理学においても量子物理学においても、電子の電荷は理論から導出できず、むしろ理論に組み入れなければならないものだったのである(これは、ハイゼンベルクとシュレーディンガーの量子論が、電子のスピンを取り込まなければならなかった事情と似ている。ただし、ディラックの理論からは自然に電子のスピンが出てくる)。
量子論がこの状況に追い討ちをかけたのは、量子論には微細構造定数αが含まれているためである。要するに、微細構造定数は電子の電荷(e)を他の二つの基礎定数、すなわち、きわめて小さなプランク定数h(宇宙における測定可能な最小の領域を定めるとともに、原子の世界を扱う量子論を特徴づけている定数)と、きわめて大きな光速c(宇宙を扱う相対性理論を特徴づけている定数)に結びつけていたのである。
パウリはあい変わらず、微細構造定数と量子論に現われる無限大との関連に頭を悩ませていた。この問題はどうやっても消えてくれないように思えた。彼は一九三四年四月に、「一三七がうまく処理できれば、すべてが申し分のない状態になるのだが」とハイゼンベルクへの手紙に書いた。六月には、「なぜ1/137なのか。この大問題をずっと考えている」と伝えている。
この年の十一月にチューリヒで行なった講演のなかで、パウリは量子電磁力学につきまとっている無限大の問題を取り除くことの重要性を強調するとともに、量子電磁力学がわれわれの空間と時間の理解にどのように関係しているのかに聴衆の注意を向けた。その上で彼は、この無限大という問題を解決するには、「無次元の数〔1/137〕の数値的な重要性を解釈する」必要があるだろうと述べた。
いったい何があったのだろう。なぜパウリは突然、「一三七」についての自身の考えを語りはじめたのだろう。もしかすると、ユングの精神分析が神秘主義的な思索に対するパウリの心を開かせる結果になったのかもしれない。
一九三五年には、ドイツを逃れてイギリスのケンブリッジ大学に身を寄せていたマックス・ボルンが、「謎めいた数一三七」という題の論考を発表した。ボルンといえばゲッティンゲン大学でパウリの師だった人物である。そのボルンは、なぜ「一三七」が科学者たちにこれほど大きな神秘的な影響力を及ぼすのかを探っていた。ボルンによればその主たる理由は、微細構造定数が、科学研究における究極の目標、すなわち、きわめて大きな世界(宇宙)を探究する相対性理論と極微の世界(原子の世界)を探究する量子論との統合を達成する手立てになるように思えたことにある。
ボルンは論考のなかで、「一三七」という数を「神秘的な」ものにしている性質をいくつか調べているが、特に注目したのは、次元をもつ基礎定数から構成されているのに、微細構造定数自体は無次元なことだった。微細構造定数は、宇宙がいまある姿に進化する上でもきわめて重要だった。
ボルンは次のように書いている。「もしα〔微細構造定数〕の値が実際のそれよりも大きかったら、物質とエーテル〔真空、非実在〕を区別することは不可能で、自然法則を見つけ出すわれわれの仕事は、望みのないくらい困難なものになっていただろう。にもかかわらず、αがまさに1/137という値をもつという事実が偶然によるものでないのは確実で、そのこと自体が自然法則なのである。この数を説明することが自然哲学の中心をなす問題でなければならないのは明らかである」。
一九五五年にスイス連邦工科大学(ETH)の創立100周年記念式典が催された際、パウリはグローリア通りにある物理学科の大講義室に集まった大勢の聴衆を前に、「今日の物理学の問題」をテーマに講演をした。いつもの講演とは違って、今回のパウリは準備してきた原稿を見ながら話を進めた。だが、これではうまく話ができないことがはっきりわかった。パウリは大袈裟な仕草で原稿を脇に放り出すと、即興で力を込めて熱っぽく語りはじめた。話の核心は、微細構造定数がきわめて大きな重要性をもちながら、どれほど不可解で理解しがたいものであるかという点にあった。微細構造定数は単に電子どうしの相互作用の仕方を示しているだけでもないし、測定された定数にとどまるものでもない。科学者が何をなすべきかといえば、それは「微細構造定数を、理論物理学における文字どおりの重要問題であると認めること」である。会場に割れるような拍手が湧き起こった。
パウリとハイゼンベルクは、原子物理学におけるスペクトル線を理解する上でも、また、電子と光の相互作用の仕方を扱う量子電磁力学にとっても、微細構造定数を理解することが根本的な重要性をもつことをはっきり認識していた。そこで二人は、微細構造定数を最初から量子論に取り入れるのではなく、逆に量子論から微細構造定数を導いてやろうと決意した。彼らの考えでは、微細構造定数の導出が可能な量子電磁力学の形式を見つけることができれば、そこには理論を台なしにしてしまう無限大になる量は含まれていないはずだった。だが、どうやってもうまくいかなかった。物理学者たちを悩ませているさらに根源的な問題--微細構造定数をどのようにして導くかにとどまらず、素粒子の質量をどう説明すればいいのか--は現在にいたっても解決されていない。
アメリカの物理学者リチャード・ファインマンも、「一三七」について論じたエディントンの哲学論文と科学論文を調べたことがある。そのファインマンは一九八五年の著書『光と物質のふしぎな理論』のなかで、彼独特の語り口で次のように述べている。
1/137は50年以上も前に発見されて以降ずっと謎のままであり、有能な理論物理学者はおしなべて、この数を自室の壁に貼って頭を悩ませている。この数がどうして現われるのか、すぐにでもその起源を知りたいと思うだろうが……だれにもわからないのだ。1/137は物理学におけるもっとも忌まわしい謎の一つである。われわれのところにやってきて強大な影響力を及ぼしているくせに、人間にはまったく理解不能な魔法の数なのだ。
そもそも、この魔法の数はどこから現われたのだろう。発見したのはゾンマーフェルトだが、彼はどのようにしてこの数を見つけたのだろう。ゾンマーフェルトがたどった思考の過程をかいま見るためには、ちょっとばかり数学の旅をするより仕方がない。
スペクトル線の構造の問題をじっくり考えていたゾンマーフェルトは、原子を微小な太陽系に模したボーアの原子理論に現われる式を別の角度から眺めてみた。その式とは、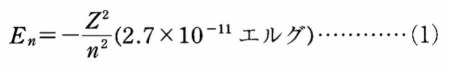
である。これは、水素原子の電子やアルカリ金属原子の最外殻の電子のように、孤立電子のエネルギー準位を与える式である。アルカリ金属原子は内殻がすべて電子で満杯の状態、すなわち閉殻になっており、最外殻の一個の電子だけが化学反応に関与するという点で水素原子と似ている(ちなみに、パウリはアルカリ金属原子を研究していて排他原理を発見した)。エルグ(erg)はエネルギーのcgs単位である。この式は整数の量子数(主量子数)によって定まる特定の軌道を回る電子のエネルギーを表わしている。Zは原子核の陽子数で、右辺のマイナス記号は、電子が原子内に束縛されていることを示している。2.7×10^(-11)エルグというエネルギー量は、電子の電荷(e)、電子の質量(m)、プランク定数(h)を組み合わせた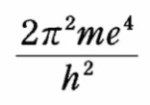
の形で(1)式に含まれていたものを算出した値である。この値は、水素原子(Z=1)の電子がもっともエネルギーの小さな軌道(n=1)にあるときのエネルギーを表わしてもいる。
ゾンマーフェルトはボーアの元の理論に手を加える必要があると結論を下した。彼の着想のすばらしさは、新たに定式化するに際して相対性理論を取り込んだ点にある。そうすれば、質量とエネルギーの等価性を述べたE=mc^2にしたがって、電子の質量が変化することを考慮に入れることになる。その結果得られたのが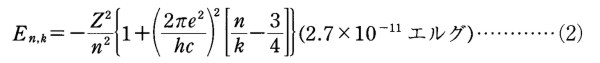
である。この新たな式には、nのほかに量子数kが加わっているが、これは電子が取りうる軌道の数が増えることを示しており、電子がより多くの軌道間で量子ジャンプをする可能性があってもおかしくないということになる。したがって、これなら原子がさらに多くのスペクトル線、すなわち微細構造を示す可能性があってもおかしくないのである。
式(2)の{ }を外せば、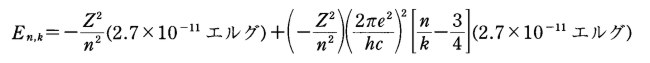
となるから、右辺の第一項は元のボーアの理論の式(1)と同じである。だが今回の式にはさらに一つ項が加わっている。
この二番目の項に二乗の形でかかっているという記号の組み合わせは、これまで物理学者のだれ一人お目にかかったことのないものだった。ゾンマーフェルトは電子の電荷、プランク定数、真空中の光速の値をもとに、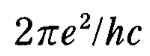
が0.00729になることを導いた。この定数が原子のスペクトル線の分裂--すなわち微細構造--のスケールを決めていることに気づいた彼は、これに微細構造定数の名を与えた。
この数が式に現われるのは、この数が原子のなかに存在するからなのである。微細構造定数が原子の実在の一部なのは、原子にはスペクトル線の微細構造が内包されているからである。それまでも、物理学者たちは微細構造が存在することは知っていた。彼らは実際に微細構造を測定していたが、実験結果と一致する微細構造の式を手にしていなかった。それをいま、次の形で手にしたのである。
式(2)の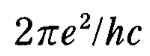
を1/137で置き換えた式(3)は、実験で観察される微細構造を完璧に表現していた。
また、「黄金比」と数学的に関係づけられるフィボナッチ数列の項を利用しても「一三七」を表わすことができる。フィボナッチ数列は整数からなる数列で、最初の項を0、次の項を1と定め、それ以降の項は前の二つの項の和になっている。したがって、フィボナッチ数列は0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987……という具合につづいていく。
この数列の隣り合う二つの項の比をとっていくと、1/1=1.000000、2/1=2.000000、5/3=1.666666……、987/610=1.618033というように、黄金比の値である1.6180339837……に到達する(フィボナッチ数列の隣り合う 2項の比は黄金比に収束する)。古代ギリシア以降、黄金比による分割(黄金分割)は、もっとも調和のとれた分割法として画家や建築家の指針になってきた。ちなみに、古代エジプトのピラミッドやアテネのパルテノン神殿、現代の国連ビルにも黄金分割が見られる。
フィボナッチ数列の名は、一三世紀にこの数列を表わす漸化式の問題を取り上げたイタリアの数学者フィボナッチ(ピサのレオナルド、レオナルド・ピサーノともいう)にちなんで名づけられた。フィボナッチ数列と黄金比の関係に気づいたのはケプラーである。
フィボナッチ数は、先に述べたような関係があるので、「一三七」を黄金比に換算すれば、「一三七」を表わすどんな式でもフィボナッチ数を使って書き直すことができる。もっともそんなことをしても、単にある特定の数のあいだに深遠な関係があるというだけのことで、それ以上のものが得られるかどうかは定かでない。
しかし、円を考えに入れて一三七を角度と見なすと円は360度であることから
360÷α=2.627048…(小数点以下は循環小数)
となり黄金比であるφ^2=2.618034……に近い数になる。
あるいは137ではなく137.51にすると、
(360-137.51)÷137.51=1.61799
となってφの値1.618034……に近くなる。
フィボナッチ数を組み合わせて「一三七」を作りだしても、残念ながらそこに「科学的」根拠があるわけではない。それなのに、人々はあいも変わらず「一三七」を何とかしようとして、もどかしい思いをしている。それどころか「一三七」は熱中や崇拝の対象になってしまっている。
「一三七」を追求し続けたパウリは、1958年一二月一五日チューリッヒの赤十字病院の一三七号室で膵臓がんにより息を引き取った。
今まで6回に及ぶこのブログでの書き込みを顧みると、「一三七」という数と、パウリが微細構造定数を量子電磁力学から導こうと取り付かれたよういになったことに行き着く。「一三七」を導くという問題は、現在においてもいまだ未解決である。
パウリが一九五四年十一月に見た夢は非常に奇妙なものだった。当時の彼は、昼間は物理学における対称性の
問題と、心理学における対称性の問題(互いに鏡像関係にある意識と無意識の問題)に没頭していた。したがっ
て当然のように、夢中になっていた問題が形を変えて夢のなかにも現われた。
その夢のなかのパウリは、一人の暗い色の女とともに、鏡を使った光の反射などの実験が行なわれている部屋
のなかにいる。室内にいる「他の人たち」は鏡に映った反射像を現実の物体だと考えているが、パウリと暗い色
の女はそれが鏡像にすぎないことを知っている。そして、暗い色の女は時折、『中国人の女』に姿を変える。
パウリは、夢のなかの「他の人たち」は集団が共有している見解を象徴しているのだろうと推測した。そし
て、パウリが懸命に取り組んでいた難問は、「この夢では『物体』と『鏡による反射像』のあいだに対称性がな
い」ことであった。なぜなら、この夢の核心はまさに、両者を別のものとして区別することだったからである。
夢のなかのパウリには、現実の物体のように見えるものが鏡に映った像にすぎないとわかっていても、「他の人
たち」はそれが理解できない。この夢は鏡映対称性を完全に欠いている。だが、当時としては鏡映対称性の欠如
などありえないことであった。
一九五二年から一九五六年にかけて、物理学の世界では、このテーマに焦点を当てるのがもっともだと思われ
るような目立った進展は何もなかった。彼が「中国人の女」の夢を見て、「この問題には心理学的な要囚が絡ん
でいるに違いない」と考えるようになるのは、その二年後のことである。
パウリは時間の反転を調べることで鏡映対称性の研究に着手した。彼は時間を記号Tで表わし、それにマイナ
スの符号をつけた。これは要するに、時間を逆向きに進ませるということである(時間が逆に進むのを想像する
のは容易ではないが、素粒子の世界では実際に、はじめの状態と終わりの状態が入れ替わった反応、すなわち時
間を反転させた反応が生じる)。時間が逆向きに流れるとき、その世界では、もともとは右方向に運動していた
粒子は左方向に運動している。粒子の速度も反転しているのだ。時間反転則によれば、時間を反転させても物理
法則は不変に保たれる。これを時間反転不変性という。要するに、運動している素粒子の集団の状態は、時間が
反転している同じ素粒子集団の状態と何ら違いがないということである。時間反転不変性は、特別な状態にある
物体の集団がもつ性質ではなく、その集団の異なる二つの状態に見られる性質である。言いかえれば、電子のス
ピンとは違って、時間反転不変性は粒子固有のものではない。
鏡映対称性の問題を論じたパウリの講演にヒントを得て、時間反転に対する対称性と他の二つの対称性の関係
の研究に向かう物理学者も現われた。その二つとは、パリティ変換(P)と荷電共役変換(C)に対する対称性
である。パリティ変換は時間座標を変えずに空間座標の符号を変える操作であり、簡単に言えば、この変換によ
って右と左が入れ替わった鏡像が得られる。古典物理学、量子物理学のいずれにおいてもパリティ保存則が成り
立ち、すべての物理学的系で右と左の違いの影響はないとされていた。物理学者たちは、原子の系のパリティ対
称性は時空内の系の位置とは無関係で、どんな相互作用のもとでも不変に保たれると考えていた。パリティ保存
則が成立していれば、何らかの実験を行なって得られる結果は、その実験を鏡に映して見たときとまったく同じ
で、鏡には完全な反射像が生じる。これをパリティ不変性、あるいは鏡映対称性と呼んでいる。
もう少し厳密に言えば、パリティ保存則とは要するに、物理学の法則は左右の入れ替え(空間の反転)に対し
て不変でなければならないということである。パリティ不変性によって原子の系のさまざまな性質を説明できた
ため、パウリが鏡映対称性の研究をはじめたころにはパリティ不変性は自明のものとされており、疑問視される
ことはなかった。
鏡像の研究に着手してから二年を経た一九五四年、パウリはこの問題をさらに深く調べてみようと決意した。
荷電共役変換(C)、パリティ変換(P)、時間の反転(T)をそれぞれ個別に調べるのではなく、この三つを
組み合わせた操作であるCPT変換を総体的に調べることにしたのである。したがってCPT変換は、粒子と反
粒子の置き換え(C)、右と左(空間)の入れ替え(P)、時間の反転(T)の操作を伴い、数学的にはこの三
つの積変換を行なうことになる。模式的に書けば(粒子⇔反粒子)×(右⇔左)×(未来⇔過去)である。CP
T変換からは、反物質が物質に取って代わり、位置座標がすべて逆になり、時間が逆に流れている世界、すなわ
ち鏡像宇宙をわれわれの宇宙と区別することは事実上不可能であるという驚くべき結果が導かれる。
パウリはCPT変換というこの複雑な概念を「C、P、Tの操作をそれぞれ個別的に取り上げる場合に比べる
と、……この三つの操作すべてを組み合わせたCPT変換のほうがはるかに一般的な仮定のもとで正確である」
と述べている。CPT変換では半整数のスピンをもつ粒子の集団と整数のスピンをもつ粒子の集団を別々に扱わ
なければならないので、この変換を数学によって取り扱う際には排他原理が重要な役割を果たした。
一九五六年六月、実験物理学者のフレデリック・ライネスとクライド・コーワンが劇的な発見を成しとげた。
ついに、パウリが26年前に存在を予測したニュートリノが実際に存在することを、実験によって証明したので
ある。そして、パウリは世界中から「ニュートリノの生みの親」として賞賛を浴び、ニュートリノについての講
演依頼が殺到した。
同じ一九五六年の六月に、二人の中国系アメリカ人の物理学者、T・D・リーとC・N・ヤンが一篇の論稿を
パウリのもとに送ってきた。そのなかで二人は、もしかすると鏡映対称性(パリティ変換に対する不変性)がつ
ねに保存されるとはかぎらないかもしれないと述べていた。
科学文献を調べたりーとヤンは、パリティ保存則を裏づける実験的証拠が実際にはほとんどなく、パリティ保
存則が普遍的なものではないと考えれば、高エネルギー物理学のいくつかの不可解な現象を理解できるようにな
ると確信していた。彼らは自分たちの考えを検証するための具体的な実験も提案していた。パリティ保存則が破
れているかもしれないと提案するとは、とんでもない話だった。パウリはくすくす笑って彼らの論文を無視し
た。
にもかかわらず、リーとヤンの言い分には大きな説得力があったため、興味をもつようになって実験に着手す
る物理学者も現われた。パウリは翌一九五七年一月一七日にヴァイスコップ宛に書いた手紙のなかで、実験が失
敗に終わるほうに「大金を賭けてもいい」と述べていた。前日の『ニューヨークータイムズ』紙の一面に、同紙
が物理学の「中国革命」と名づけた出来事が報じられていたことなど知る由もなかった。中国出身の女性物理学
者チェン・シュン・ウーに率いられたコロンビア大学の研究グループが実に見事な実験を行ない、弱い相互作用
ではパリティが破れている(パリティ変換に対する不変性が成立しない)ことを疑問の余地なく実証したのであ
る。かくしてパリティ保存則は弱い相互作用ではくつがえされた。それはパウリにとって青天の霹靂にも等しい
衝撃的な出来事だった。
言うまでもないことだが、まわりを見回せば、人間の身体だって左右対称になっていない。だが物理学者たち
はそれまでずっと、物理学の法則には鏡映対称性があって当然だと決めてかかっていた。物理学の式はどんな場
合もこれを前提にして書かれてきた。それが少なくとも原子のレべルでは、鏡映対称性がいつでも当てはまると
はかぎらないことが明らかになった。
「自然は数学のような正確無比のものではなく、われわれが考えていたようなものとは違うのだろう」と、パ
ウリはフィールツヘの手紙にこう書いている。パリティの破れの発見は、ピュタゴラス学派の人々が2の平方根
が有理数にならないのを知ったのと同じように、状況を一変させる出来事だった。
それでもパウリは、対称性を有する原理や法則のほうが一般的でなければならないと固く信じていた。そうし
た原理や法則を見つける手立ては論理によって得られるだけでなく、思想の不合理な側面にも見いだせる。「私
の場合、数学と神秘主義が入り混じった見方は、物理学における重要な成果につながっており、いまでも卓越し
た地位を占めている」と彼は言う。
パウリは一九四一年にカリフォルニア大学でウーと会ったことがあり、ユングには彼女のことを「実験物理学
者としても、知性にあふれる若くてきれいな中国人女性としても」印象的だったと知らせている。ウーは一九三
六年に渡米し、カリフォルニア大学で研究をしたあとコロンビア大学に移った。彼女は、まさに、パリティ保存
則を検証する超精密実験の試みには欠かせない人物だったのである。
パウリはウーヘの手紙に、「私がいままで、これ〔パリティの破れ〕が文字どおり起こりうることを受け入れ
られなかったのは、なぜ鏡映対称性の制約が『弱い』相互作用にのみ現われ、『強い』相互作用では現われない
のかという疑問のためでした」と書いている。また、ユングヘの手紙では、パウリは想像力に富む表現で「結局
のところ神は軽い左利きでした」との言葉を残している。
古典的な描像で言えば、ニュートリノの自転(スピン)は一方向にかぎられている。鏡に映ったニュートリノ
もやはり同じ方向に自転しているのである。われわれが日常使うねじの大半は右ねじで、時計回りに回転させる
と前に進んでいく。ニュートリノはこの意味では左ねじである。というのも、ニュートリノは運動方向に対して
左回りの自転をしているからである。だから「神は左利き」なのだが、それでも軽い左利きなのは、神が左手だ
けを使うのはパリティが破れている弱い相互作用(ニュートリノが主役を演じる相互作用)にかぎられているた
めである。
パリティの破れにまつわる出来事が共時性の見事な一例であることに、パウリが気づかないはずはなかった。
パウリの夢のなかでは「中国人の女」が重要な役割を担っていたが、特にそれが顕著に表われていたのが、鏡と
鏡による反射像を伴う夢であった。現実の世界では、中国人の女性研究者が物理学におけるパリティ保存則、す
なわち鏡映対称性をくつがえす実験を行なったのである。パウリはユングに、物理学におけるこの「中国革命」
がどれほど「ショック」だったかを述べていた。
一九三五年ころから、パウリは時折、「物理学に由来する用語や概念が定性的・比喩的意味で--すなわち、象徴的な意味で--現われる」夢や白昼夢を見るようになった。彼はこの象徴的現われを「背景物理」と呼んでいる。彼はこうした夢に登場するシンボルと、ケプラーの著作などの「科学用語や科学概念がかなり未熟な段階にあった」一七世紀の文献で見た象徴的図像とのあいだに類似性があることに思い当たった。
この類似性を調べているとき、パウリは科学について何の知識もない人々が、しばしば同じようなイメージを作りだしていたのを発見した。彼はこの事実をもとに、自分の見た夢は結局のところ無意味なものでもなければ根拠のないものでもないとの結論を下した。こうした類似性は、「背景物理が元型的性質をもつこと」の証拠のように思えたのである。物理学と心理学は互いに補完しあう相補的な関係にあるので、「どちらにとっても同じように有効な手法があり、それを利用すれば、心理学者たちは『裏から』(すなわち、元型の研究を通して)物理学の世界に導かれるに違いない」とパウリは確信した。言いかえれば、物理学の概念や用語のシンボルが時代を超えて広く見られるという事実は、原子物理学のシンボルが元型に由来することの確固たる証拠を与えているように思われたのである。
パウリは「背景物理」の一例としては、スペクトル線の微細構造を取り上げている。彼が見つけようとしていたのは、夢に隠されている意味、すなわち純然たる物理学を超えた「第二の意味」である。その意味を解き明かすには、パウリは物理学者だけでなく心理学者にも理解可能な「中性言語」を探しだし、微細構造という概念をその言葉に翻訳しなければならない。彼が特に興味をもったのは二重線--微細構造が二本のスペクトル線となって現われる--の夢である。パウリは二重線への分裂を、子どもの誕生の瞬間に母体と一つだったものが二つになるという経験と関連づけた。誕生の瞬間、胎児はスペクトル線が分裂して二重線になるのと同じように、一個の独立した存在となる。さらに二重線は、「新たに生まれた意識の内容が無意識の鏡像を表わす」--無意識を映す鏡としての意識--という精神的な意味での二重化とも結びつけられる。
パウリは一九五三年に、とりわけ印象に残るスペクトル線の夢を見た。夢のなかのパウリは妻のフランカとある実験を観察していて、実験の結果は写真板上にスペクトル線として現われる。スペクトル線のうちの一本は微細構造をもっていた。
パウリはこの夢について、「好ましい徴候があり、二番目のスペクトル線に微細構造が見られる」、そして「この夢がどんな働きをしているかと言えば、それは無意識の内容の意識への同化のはじまりを示す」と解釈した。パウリはかなり以前から、二重線がスズメバチ(パウリにとっては大きな恐怖のもとだった)やトラに見られる、明暗が交互になった縞模様にそっくりなのに気づいていた。このパターンは対立する二つの力、光と闇の果てしない反復を表わしていた。心理学的観点から見れば、このパターンは心理状態に反復性があることの象徴だった。
この光と闇の対立の意味は、ボーアの相補性という考え方を適用すればさらに明確になる。相補性はそもそもは、互いに補完しあう関係にある相補的な対--たとえば波動と粒子--のあいだの対立という観点に立てば量子力学的現象の理解が可能であることを述べたものだった。とはいえボーアは、相補性が物理学にとどまるものでなく、あらゆる生命現象の理解に不可欠のものだと確信していた。生命現象では生と死、愛と憎しみ、陰と陽といった相補的な対が重要な役割を演じているのである。パウリは一九四八年のエッセイのなかで、こうしたことはいずれも、「対立物からなる相補的な対には、これに対応するさらに深遠な元型があることを指し示しているように思われる」と述べている。さらに言えば、こうした相補的な対は、二本に分裂するスペクトル線によって象徴化され、分裂の幅は『一三七』という数で特徴づけられる。このことが、『一三七』は元型的な数であるというパウリの信念をさらに強固なものにした。
相補的な対という見方をすることで、パウリは中国の書『易経』の根本をなす、線によるパターンのことも思い出した。
中国に古くから伝わる占いである易が現在のような形になったのは、周(紀元前1050?~前256)の時代だったとされている。『易経』はその易のための書で、ユングは、『易経』は西欧の因果律という考え方を用いたのでは理解できない偶然の出来事の本質を見抜いていると考えていた。
図:上左;八卦爻と太極、上右;後天八卦図、下二つは先天図・後天図の配置
『易経』の本文経(けい)は、卦(「け」ともいう)と呼ばれる64種類の象徴的記号と、その意味を解説した占断の言葉で構成されている。卦は陰の象徴である「--」と陽の象徴である「――」の棒、爻(こう)を三本組み合わせて作った八種類のパターン(八卦)を上下に二つ重ね合わせたものである。占者は筮竹(ぜいちく)と呼ばれる50本の細い竹の棒を使って卦を立てる。卦が得られると、占者はそれをもとに占断を下す。それぞれの卦を解説した『易経』の占断の言葉はきわめて格言に富んでおり、慎重な解釈が必要とされる。
易による予言は多くの要因に関係している。もっとも重要なのは、われわれを取り巻いている世界は善と悪、光と闇、愛と憎しみ、男と女などの二元性を意味する対立物……すなわち陰と陽……のせめぎ合いから生じるということである。ユングは卦に込められたメッセージが西欧の物理学では説明できない「現在という瞬間」の隠された性質、すなわち偶然の出来事の同時性の意味を明らかにすると考えていた。
パウリも「夢に出てきた場面を解釈するときに」『易経』の文言を参考にしていた。パウリが卦による占いをどこまで理解していたかはともかく、彼は一つの爻を描くのには三回の操作が必要なのに、「その結果は4で割り切れる数によっている」と述べている……またしても三と四なのだ。しかも、64(卦の数)は4を三回掛け合わせた(4の三乗)数である。このことがパウリを宇宙時計の夢に立ち返らせた。宇宙時計の夢では、「三と四に満ちあふれたモチーフが、調和の感覚を与える主たる源になっていた」。
かつては、物質は万物を生みだす根源であると考えられた。これに対して現代の物理学では、物質は完全に「はかない」存在になった。粒子と反粒子が自然に対生成したり対消滅したりするように、物質は生まれることも消滅してしまうこともあるからである。反粒子の一つに、電子の反粒子である陽電子(ポジトロン)がある。陽電子の性質は、負の電荷ではなく正の電荷をもつという点を除けば、電子とまったく同じである。粒子と反粒子が出会うと、両者は一瞬のうちに消滅して光や他の粒子に変わる。ディラックの有名な方程式(ディラック方程式)によって最初にその存在が予測されていた陽電子は、一九三二年に実験室で発見された。
パウリは、物質を特別な存在と見なして打ち建てられた生命観には何の根拠もないと考えていたが、粒子の対生成と対消滅は、彼のその見解を裏づけるものだった。アインシュタインは、彼が発見した質量――すなわち物質--とエネルギーの等価性をE=mc^2によって象徴的に表わした。この式では、質量が形状をもたないエネルギーで置き換えられている。エネルギーは形態を変えることはあっても消滅することはないので、時間を超えた存在と言ってもいい。その結果、エネルギーの総量はつねに不変である。これをエネルギー保存則と呼んでいる。だが相対性理論からは、質量については保存則が成り立たないという驚くべき結果が導かれる。
エネルギーは時間を超越しているとも言えるが、その時間と空間のなかへの現われ方は独特である。量子物理学によれば、原子のスペクトル線として観測される光のエネルギーは、その光の振動数(1秒間に何回振動しているか)に比例する。
電子がエネルギーの大きい軌道から小さい軌道へ飛躍する際に生じるスペクトル線のエネルギーを正確に知ろうとすればするほど、電子の遷移に要した時間を正確に計測することができなくなる。ハイゼンベルクが最初に粒子の位置と運動量の測定で発見したのと同じく、エネルギーと時間のあいだにも不確定性関係(不確定性原理)がある。
パウリはエネルギーと時間の二つの座標軸を「不滅のエネルギーと運動量」に対する「限定された時空的過程」と表わし、程度の違いこそあれ、各々の微小部分はつねに存在しているので、エネルギーと時間は実在の相補的側面であると見なした。
パウリはスペクトル線の分裂の夢を見たことで、スペクトル線の振動数、なかでも二重線の振動数と意識・無意識などの対立物の対どうしの緊張とのあいだに、何らかの関連があると確信するようになった。エネルギーは時間の枠外に存在していて、限定された空間と時間の幅で生起する過程に対して相補的関係にあるが、同じように、元型的な心(時間を超越した集合的無意識)とわれわれが個人的に有している意識的な心、すなわち自我とのあいたにも相補性がある。前者が時間の全体にわたって存在するのに対して、後者の存在は日常生活の特定の時間幅にかぎられるからである。
一九四八年の春分のころ、パウリは二つの夢を見た。その二つの夢は数学記号だらけだった。そのうちの一つには、マイナス1(-1)の平方根(√-1)のiが登場する。iはわれわれが日常生活で使っている数--いわゆる実数--とは異なることから「虚数」と呼ばれるが、複雑な式を虚数iを利用して表わすと単純な形になる場合がある。
また、もう一方の夢では、女がパウリに一羽の鳥をもってくる。鳥は卵を一つ産み落とすが、しばらくするとそれは割れて二つになる。そのとき夢のなかのパウリは、自分も卵を一つ手にしていて、卵は全部で三つになることに気づく。すると突然、手にしていた卵が二つに割れる。いまでは卵は四つになった。四つが一組になって姿を現わしたのだ。パウリが見ている前で、四つの卵は数学記号に形を変える。四つの数学記号は左右隣り合わせの二つのグループに分かれていて、一方のグループではcos(δ/2)が二つ上下に並び、もう一方ではsin(δ/2)が上下に並んでいる。コサイン(cos)、サイン(sin)は直角三角形の二辺の長さの比を与える量、デルタ(δ)は三角形の二辺が作る角度である。夢はさらにつづき、これら四つの数学記号はiによって合体し、数学者にはお馴染みの次の形の式になる。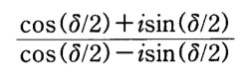
夢のなかのパウリはこの式を次の方程式に変える。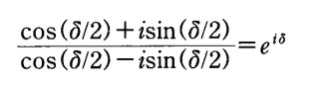
eは「自然対数の底」で、その値は2.71828…とどこまでもつづく小数になり(eは無理数と呼ばれる数の一つ。無理数は小数で表わすと循環しない無限小数になる)、e^iδの絶対値は1である。このように、四つの要素の組み合わせにiを挿入することで統一がもたらされた。
夢に出てきた卵のことを熟考したパウリは、卵が割れて増えていく過程が、一七〇〇年ほど前の女性錬金術師マリア・プロフェティサの言葉、「一は二となり、二は三となり、第三のものから全一なる第四のものが生ずる」にぴったり符合することに気づいた。パウリが注目したのは、この変容が「私の場合は例によって数学を通して生じた」ことである。
パウリがこの夢全体に対して与えた解釈は、数学とは大きくかけ離れたものだった。パウリはユングに自身の解釈を伝え、e^iδで表わされる数がすべて半径1の円周上に載ることを説明した。iという数学記号がもつ力によって、マンダラが円の形をとって現われたのである。夢のなかのiには「対立物の対(対立する二つのグループに配置されたコサイン関数とサイン関数)を結合するという理性を超えた働きがあり、それによって一体性を生みだす」。それどころか、eもやはり理性を超えた無理数の一つなのだ。これらの事実は、数学が「〔自然を〕象徴的に記述するのにとりわけ優れている」ことを示している。
数学記号は、直観に反する量子の世界の特性、たとえば、どうやっても図に示すことが不可能な波動と粒子の二重性などを一体のものにして表わすための申し分のない手段なのである。
さらに熟考を重ねたパウリは、次々に割れていく卵は分裂するスペクトル線のアナロジーであるとの考えを提示した。精度の高い分光器を使ってスペクトル線の微細構造を詳しく調べれば、一本に見えた線が実際には二本の線からなり、線と線との間隔が『一三七』という数によって特徴づけられていることがわかる。だとすると、物理学では4ではなく2が根源的な数ということになるのだろうか。物理学にも心理学にも相補的な関係にある対立物があり、それらは心のなかでも二が支配的であることを示唆していた。だが、パウリの夢に4--四つ組--が現われたことは、物質的世界と、物質的世界についての意識的知識、さらには無意識が一体のものであることを示していた。パウリによる第四の量子数の発見は、まさしくこの一体性が必要であることを示しており、したがって、第四の量子数は最初は意外に思われたとはいえ、四が完全性の元型であるとすれば、その存在は最初から予想されて当然だったのである。
パウリの夢のなかでさまざまな要素を統合した-1平方根iは、シュレーディンガーの波動関数(シュレーディンガー方程式の解)にも現われる。シュレーディンガーの波動関数は独立変数、従属変数のいずれもが複素数(a,bを実数として、a+ibの形で表わされる数)の複素関数で、量子物理学における粒子の位置の観測結果と不可分の関係にあるだけでなく、物質の波動としての性質と粒子としての性質を統一的に表わしている。
いずれにせよ、iによって四つの要素が統合される夢を見たことで、量子物理学はさらに包括的で壮大な世界像の一部を形成しなければならないというパウリの確信はいっそう強まった。量子物理学は数学によって記述できる現象にしか言及しておらず、注目したのももっぱら実験室で測定可能な量にかぎられていた。意識などの観念を考慮に入れることはなかったのである。
今回はパウリの夢の中に出てきた「宇宙時計」についてユングの考察を交えて書くことにしました。ユングは物理学者のパウリとともに共時性(シンクロニシティー=意味のある偶然の一致)に関する研究を発表しています。この二人が、物理学に関する「数」を巡る旅の始まりを、今回のブログ記事で取り上げますので、少し長い文章になってしまいました。物理学の発想を追求するためには、とても重要なところではないかという気が致しましたので、申し訳ありませんがしばらくお付き合い下さい。
パウリがふたたびユングの書斎に顔を出したのは、一九三二年の十一月であった。このとき以降、二人は毎週月曜日の午後に一時間前後の時間をとって、定期的に面談を行なうようになった。パウリはそれまでも自分の見た夢を記録していたが、一九三四年にユングとの面談を終えるまでに、さらに多くの夢が記録に加わり、その数は1000を超えることになる。ユングは一九三五年にロンドンで行なった講演のなかで、「優秀な科学者として非常に有名な若い男性」が見た夢の話を非常にうれしそうに「彼の夢には信じられないほどの一連の元型的イメージが含まれていた」と報告している。
ユングはパウリが記録した多数の夢のなかから400を取り上げて詳細に検討している。ユングが選びだしたのは、彼が「個性化」と呼んだ過程の例証となる夢である。個性化はユング学派には特別な意味をもつ用語で、各人が個性的人格を発達させる過程を指す。精神分析の観点からは、個性化が生じるのは、患者の意識と無意識がバランスのとれた状態に達したときであるとされる。この状態に到達した徴候として、患者はマンダラの夢を見るようになる。
個性化が実現した状態では、四つの心理学的機能――思考、感情、直観、感覚――は完全に意識されており、これら四つが合わさって統一された全体を作りあげている。ユングがパウリの分析に着手する以前の段階では、パウリの意識のなかで卓越していたのは思考機能であった。彼の感情機能は完全に無意識のなかに沈んでおり、感覚機能と直観機能も無意識のなかに半ば沈んだ状態になっていた。とことん知性に訴える人間で、自分の感情というものをまったく理解していない――ユングは心理学的に見たパウリの状態をこのように描いていた(図1参照)。
図1:パウリの意識の四つの機能を示した図。優越機能である思考は円の上半分を占めている。劣等機能である感情は暗いほうの半円に位置している。感覚と直観の二つの副機能は半ば明るく半ば暗い。
パウリが見る夢は時とともに変化していったが、かなり早い段階から、パターンが生じるように円が姿を現わしていた。最初に現われたのは自分の尾に食らいついているウロボロスで、ユングはこれをマンダラの原始的形態であると解した。ついで、円はもっと進化した形をとって、永久機関の夢、すなわち永遠に動きつづける振り子時計の夢のなかにふたたび姿を現わした。永遠に動きつづけるものは、永遠の円運動をするのである。そのあとパウリは恐ろしい夢を見た。人々が正方形のまわりを歩き回っていて、正方形の中心では動物の肉塊から人間の頭部が創造されている夢である。この夢では、恐ろしい出来事は円の内部ではなく正方形の内部で起きているが、ユングは、これはパウリの夢にしばしば登場する四人の人物、すなわち分析心理学で言う四つの機能を表わしていると解釈し、ことによると、パウリが発見した四つの量子数も表わしているのかもしれないと述べている。
ユングは円と正方形に関して、「男と女を囲んでまるい円を描き、その円をもとに四角形を、四角形をもとに三角形を得よ。さらに円を描けば哲学者の石を得ん」という錬金術書の一節を引いているが、これはラマ教のマンダラを描写したものにもなっている。さらに、もっとも根源的なレヴェルで見れば、この記述は、正方形の内部に築いた半球状の小山(覆鉢)からなる仏教の聖建造物、ストゥーパ(仏舎利塔)の平面図を表わしている。礼拝する信者たちはストゥーパのまわりをつねに時計方向、すなわち右回りに歩く。左回りは不吉とされているからである。ユングはこれに関して、右は意識へと通じ、左は無意識に通じるからだと説明している。マンダラの絵は、正方形の内部に円と東西南北の四方位が含まれており、したがって人間の生のすべてもここに含まれていることをはっきりと示している(図2参照)。
図2:金剛界曼陀羅(マンダラ))
パウリの夢に現われるマンダラは時とともにより完全な形をとるようになり、ユングはこの変化を、パウリが心の旅路のなかで個性化に向かって歩を進め、健全なペルソナを作りあげつつある証拠だと見なした。夢に現われるマンダラを描いたパウリの一連の絵は、彼のなかで意識と無意識がますます釣り合った状態に近づきつつあることをはっきりと示していた。
図3:パウリの夢に出てきたいびつなマンダラ
ユングに指示されて夢の記録をつづけていたパウリは、ある日はじめて不正確な形のマンダラの夢を見た。パウリは夢のなかで何とか対称な形にしようとするが、失敗に終わってしまう。そのマンダラは、水平方向の腕木のほうが垂直方向の腕木よりも長かった。ユングはこのマンダラには高さと深さが欠けていると解釈した。言いかえれば、いまだに自我がパウリの心を支配しているということである。夢に現われたこのマンダラのそれぞれの腕木には、パウリが円として描いた鉢状の容器がある。どの容器も液体で満たされている。一つの容器は赤、もう一つは黄色、さらにもう一つは緑の液体が入っているが、第四の基本色である青が欠けているために、第四の容器に入っているのは色のついていない液体である(錬金術師たちの考えでは、虹はアリストテレスの四元素に対応する四色、赤〔火〕、黄色〔空気〕、緑〔水〕、青〔土〕から構成されていた)。パウリの夢に出てきたこのマンダラは、いびつであったばかりか不完全でもあった(図3参照)。
科学に携わるなかで、パウリは視覚的想像の重要性を十分に承知していた。一九三〇年代の物理学はあい変わらず「精神的・人間的混乱期」にあった。直観に反する原子の世界に対して、パウリがその正しいイメージを作りあげる手立てを追い求めはじめた一九二〇年代と、何ら変わるところがなかった。パウリが提唱した第四の量子数には視覚的イメージが欠落していたが、そのことが、原子を微小な太陽系になぞらえるボーアの視覚的イメージを打ち壊す一助となったのである。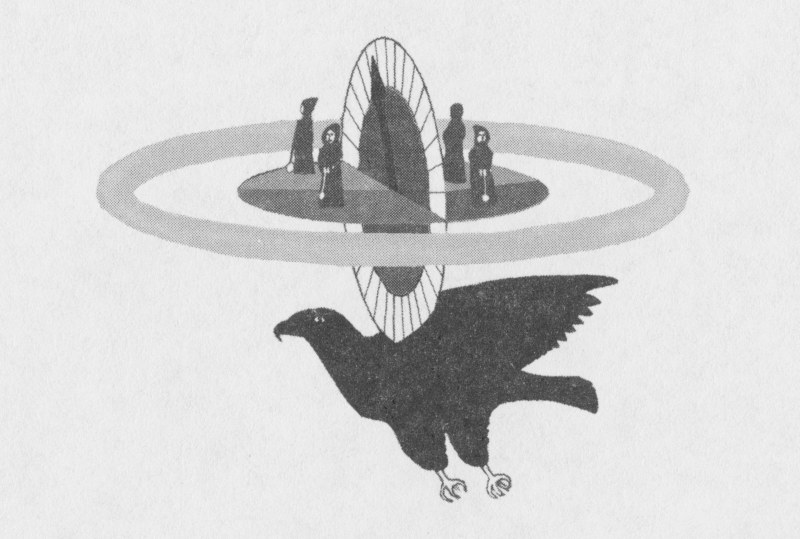
図4:パウリの夢に出てきた「宇宙時計」
パウリはそれからしばらくして、彼が「大いなる幻像」と呼んだ「宇宙時計」の夢を見た(図4参照)。彼はその幻像が「調和の極致」の印象を与え、彼自身、幸福感と穏やかな気持ちで満たされたとユングに伝えた。ユングはパウリの夢に出てきた宇宙時計を次のように描写している(上の図には、色を塗り分けていないため、色が塗ってあるものと想像して読み進んで下さい)。
共通の中心をもつ垂直の円と水平の円がある。これは宇宙時計である。この時計は黒い鳥に支えられている。垂直の円は青い円盤になっており、白の境界線で4×8の32の区画に分割されている。円盤上では指針が回転している。水平の円は四色の色で構成されている。こちらの円の上には振り子をもった小人が四人いて、円の周囲には、それを取り巻くようにリングが配置されている。このリングは以前は黒だったが、いまは黄金色である……この「時計」には三種のリズム、すなわち脈動がある。
それは次のとおりである。
1 小さな脈動 垂直になっている青い円盤上の指針は、32分の1ずつ進む。
2 中程度の脈動 青い円盤上の指針が完全に一回りする。それと同時に、水平の円が32分の1だけ回転する。
3 大きな脈動 中程度の脈動の32回分は黄金色のリングの1回転分に等しい。
だが、この時計は何を意味しているのだろう。ユングは、パウリが以前に見た夢のなかでそれとなくほのめかされていたすべてのものが、この時計に凝集されているのを認めた。以前の夢では、それらのシンボル――円、球体、正方形、回転、十字架、四元性、時間――は個別的に登場していた。今回の夢では、完全な対称性が備わっていた。
パウリの宇宙時計には三種のリズム(脈動)があった。第一は、32の区画に分割された垂直の円盤上で生じる小さな脈動である。指針は時を刻むように、一回に一区画ずつ進みながら回っていく。指針が一回りしてすべての区画を通り終えると、水平の円が32分の1回転する。これが中程度の脈動である。この水平の円が完全に1回転したとき、「大きな脈動が生じる」。黄金色のリングが1回転するのである。
青い垂直の円は、赤、緑、オレンジ、青の四つの色に分けられた水平の円と交差している。各色の四分円には異様な風体の小人が立っているが、ユングはこれらの小人を「カベイロイ」と解釈している。カベイロイは古代ギリシアに起源をもつ暗黒の神で、航海を守護する神とされている。ユングの分析心理学によれば、カベイロイがこの場にいるのは、無意識へ向かうパウリの心の旅の案内をするためだった。どのカベイロイも振り子を手にしている。そして、青い円の脈動が全過程のはじまりである。ユングは32という数の重要な役割を述べている。すなわち、32は「4」に8をかけたものなのだ。
これは奇妙に思えるかもしれない。だが、ユングはつづいて、カバラでは32という数はきわめて重要な数で、知恵を意味すると指摘している。カバラによれば、32はヘブライ語のアルファベットの数22と、セフィロトの象徴である生命の樹の枝の数10の和として表わすことができる。さらに、「創造の書」にあるように、知恵にいたる道の数も32なのである。
パウリはついに完全な形の三次元のマンダラを夢で見た。だが、ユングは当初、それが何を意味しているのかに当惑してしまった。その幻像の印象を「調和の極致」と表現したとき、パウリは何を言おうとしていたのだろう。パウリの心の全体性を意味しているように思われたが、なぜ彼はあんなにもはっきりと、いまは穏やかな気持ちだと言い切ったのだろう。ユングは、何か重要な手がかりを見落としているのだろうかと考えた。もしかすると、パウリは「調和」という言葉で音楽の調和、すなわちケプラーが用いたのと同じ意味での天球の調和のことを言おうとしていたのかもしれない。だが、夢に出てきた円はとりたてて調和を保っているというわけではなかった。いずれの円も、性質も違えば動きも異なっている。
もう一つの問題は、マンダラの中心には神聖な対象やイメージが位置しているのがつねなのに、パウリが夢で見た宇宙時計にはそうしたものがいっさいないことだった。中心にあるのは、二つの円の直径が交わってできる数学の点だけだった。実質的には何も存在しないのと同じなのである。
それでも、パウリが夢で見たマンダラ(宇宙時計)は、男性的な三位一体(三つの脈動)と女性的な四つ組み(四つの色と四人のカベイロイ)を含んでおり、両者が組み合わされば錬金術の両性具有を生みだす。ユングはパウリが物理学者であることを心に留めながら、パウリのこのイメージの宇宙論的な意味について思案をめぐらせた。このマンダラは時空の四次元の根源を象徴していると考えられるだろうか。
だが、それではあまりにも科学に偏りすぎているように思われた。ユングには、この線に沿って思索をさらに推し進めるだけの物理学の知識はなく、彼はその代わりに中世のシンボリズムに目を向けることにした。
一四世紀のノルマンの詩人ギョーム・ドーディギュルヴェルは『魂の巡礼行』の最終編のなかで、回転する49の球体で構成された天国の幻像を描写している。案内役の天使はギョームに、これら49の球体は現世の世紀を表わしているが、その世紀は通常の時間ではなく永遠の時間であると告げる。大きな黄金色の天がすべての球体を取り囲んでいる。差し渡しが90センチほどしかない青い円が、大きな黄金色の天のなかに下半分を隠した状態で静かに動いている。したがって、ここでは大きな黄金色の体系と小さな青色の体系の二つが交差している。ギョームは、青い円が天の黄金色の円に比べて非常に小さい理由を天使に尋ねる。天使に言われたとおり上を見上げたギョームは、天の王と王妃が玉座についているのを見る。
すると天使はギョームに、あの小さな青色の円は聖者の暦で、時の要素を運んでいると説明する。まさに今日は三人の聖者の祝宴の日だと天使は言い、それから急いで獣帯(黄道十二宮)の話をはじめる。ギョームに魚座、すなわち双魚宮について話をした天使は、魚座では12人の漁夫による祝祭が行なわれ、そのあと彼らは三位一体の前に姿を表わすと付言する。ギョームは完全に当惑してしまう。何よりもギョームが癪(しゃく)に思ったのは、彼が実際には三位一体の秘密を理解していなかったことだった。天使は三つの基本色である緑、赤、黄金色について話をはじめるが、しばらくすると突然話をやめて、ギョームにこれ以上質問してはいけないと命じる。こうして詩の最終編は終わり、『魂の巡礼行』も幕を閉じる。
ユングにとってギョームが描写する天の幻像は、パウリが夢で見たマンダラと、パウリを満たした至上の幸福感を解明する重要な手がかりとなった。ギョームの幻像でもパウリの夢でも、青色の円は時を表わしている。パウリのマンダラの青色の円は同じ直径のもう一つの円と交差しており、そのために、円と円とはギョームの場合よりも調和のとれた組み合わせになっている。青色の円は32の区画に均等に分割され、その上を針がカチカチと動いていくが、これは合理性を表わしており、したがって男性的な三位一体の象徴でもある。この青色の円が、交差しているもう一つの円を動かしている。後者は赤、緑、オレンジ、青の四色の部分に分けられていて、それぞれの上にカベイロイが一人ずつ、計四人立っている。こちらの円は四つ組み、すなわち四元性(四位一体)を表わしているとユングは判断した。カベイロイたちが携えている振り子は、この宇宙時計の永遠性を示している。時計のメカニズムが一体となって黄金色のリングを回転させる。この大きな円はもはや暗黒ではない。パウリの心のなかで、彼の暗黒部分である影がアニマ――彼の女性的側面――から分離され、そのため、彼のアニマはいまでは太陽のように輝いている。彼のアニマはもはや無意識のうちに埋没させられるのではなく、光を当てられるようになったのである。
青色の円の上にある時計がすべての過程を動かしている。その理由は、ここでは三つ組み(三位一体)はこの体系の三重構造のリズムからなる脈動だからである、とユングは言う。この三つ組みも、4の倍数である32にその基礎がある。円と四つ組みは、互いのなかに相手を含むように貫入しあっている。3は4のなかに含まれているのである。
パウリとギョームが同じような夢と幻像を見ても、パウリがカトリック教徒として育てられたことを考えれば、ある意味では意外ではない。中世を通して三位一体をおおっていた問題は、この三つ組みが女性的要素を締めだしていたことである。ギョームの幻像のなかで一部が欠けていた色は、小さな未発達の円の色である青だが、これは理にかなっている。青は言うまでもなく、聖母マリアがまとっているマントの色である。ここで欠けているのはマリアなのだ。
ギョームは重要な手がかりを得ていながら、その意味を理解し損ねた。それどころか、彼は王と女王が並んで玉座についているのを見ていた。だが、王キリストは彼自身が三位一体の存在ではないのか。中世の時代に生を受けたギョームは王に注目しすぎたために、女王の存在を忘れてしまった。王と女王、キリストと聖母マリアを合わせれば、結果として四、すなわち四位一体が生じる。だから天使は、ギョームが困った質問を投げかける前に姿を消してしまったのだろう。
ギョームのみならず中世のすべての哲学者にとって、問題は第四の構成要素を見つけることだった。おそらくパウリの夢が「この古くからの疑問に象徴的な答え」を与えてくれるだろうとユングは述べ、「たぶん、宇宙時計のイメージが『調和の極致』という印象を生みだした理由は、このような非常に深遠なものだったのだろう」と結んでいる。
ユングはパウリの夢に現われたマンダラの中心に何も存在しないことについて、これは「中世のキリスト教哲学で議論された重要な問題のいくつかを、数学的と言っても過言でないほど抽象的に表わしている」と結論づけた。ユングはギョームの幻像に関する自身の知識だけで、パウリの夢と、歴史をはるかにさかのぼって人々の心を虜にしてきた観念とのあいだのつながりを理解することができた。
とはいえ、四つ組み「四元性」という概念はどのようにして無意識のなかに現われることができたのだろう。意識が無意識のなかに四つ組みという概念を植え込むことなどできるはずもない。これに関してユングは、心のなかには、四つ組みという概念によって自らを表わし、個人の完成へと向かって動いていく何らかの要素があるに違いないと結論している。彼は四つ組みという概念が世界各地の先史時代の人工遺物に見られることを力説する。四つ組みという概念は、しばしば造物主と関係づけられる元型である。とはいえ、四つ組みという概念は神の実在の証拠とはけっして言えない。人間の意識のうちに「元型的な神のイメージが存在すること」を示しているにすぎないのである。
分析を受けた結果、パウリは「完全に正常で、分別をわきまえた人間になり」、酒を飲むことさえやめた、とユングは断言している。ユングは、自身の錬金術の象徴の研究が「自己の象徴の発展」を解明するのに役立った重要な分析例として、知的な若い科学者の症例の話をすることが多かった。ユングがパウリに施した分析は、物理学に新たな観点をもたらすことにもなった。
ハイゼンベルクは、一九二七年の五月に「量子論的運動学と力学の知覚的内容について」の表題を付した論文には、現代物理学における最重要級の発見の一つが含まれていた。『不確定性原理』である。
ハイゼンベルクは、量子論の曖昧さと考えられているものが、本質的には言葉の問題であるとし、常識を越えた原子の領域、「物質」が波動であると同時に「粒子」でもある世界で、「位置」や「速度」といった用語をどのように定義するかである。そして、「位置」や「運動量」(速度と質量の積)などの量子力学のいくつかの概念は、論理的推論の法則からも実験からも導くことができないと主張した。むしろわれわれがやらなければならないのは、量子力学の特異な数学を研究することだという。なぜなら、量子力学の数学はそもそもの最初から、原子の領域で位置や運動量などの用語を用いるには細心の注意を払わなければならないと警告していたからである。
また、彼は「量子論的運動学と力学の知覚的内容について」のなかで驚くべき主張をしていた。実験で電子の運動量を正確に測定すればするほど、ますます電子の位置を正確に突き止めることができなくなる、というのである。これこそ、すぐに不確定性原理の名で呼ばれることになる主張である。不確定性原理がきわめて重大だったのは、アインシュタインの相対性理論と同じく、この原理が物質的世界の本質的性質に関するわれわれの理解に異議を唱えたからであった。
ニュートン物理学の古典論の世界なら、物体の運動を観測することによって、その位置と運動量を同じ精度で求めることができる。たとえば、望遠鏡と時計を使えば、落下する石の位置と落下速度のどちらも測定できる。ごく大ざっぱに言えば、精度の限界を定めるのは、望遠鏡の十字線と時計の計時機構だけである。測定に伴う誤差を極力小さくすれば、落下する石の位置と運動量をきわめて正確に求めることができる。古典物理学では、位置の測定誤差と運動量の測定誤差との積を、原理的にはゼロにすることもできる。だが、量子力学ではこんなことはありえない。
ボーアは、電子は実験のなかで粒子と波動の二つの側面のうち、どちらか一方を見せるが、両方を同時に見せることはない。電子を波動であるかのように扱う実験を行なえば、電子は実験中、波動として振る舞い、粒子として扱えば、粒子として振る舞うだろう。こうした表と裏のような性質をボーアは「相補性」と呼んだ。
ボーアは、相補性は物理学に当てはまるだけでなく、心理学や生命そのものにも当てはまると確信していた。量子力学において言葉の問題がもたらす厄介な状況は、「基本的には、人間が概念を形成するときに主観と客観とを区別することにつきものの一般的困難に似たところがあり、相補性の根底をなす考え方が、この状況を特徴づけるのに適したものであることを期待している」とボーアは述べている。
中国の陰陽の概念と同じように、補完関係にある二つの相補的概念が実在を規定する。実験が実施されるまで、電子が波動としての特性と粒子としての特性の両方をもっていても、そこには何の矛盾もないのである。ボーアには、量子の奇妙な世界では答えが二つのうちの一つでしかないという必要はなく、電子が実際には粒子か波動のどちらかである必要もないことがわかってきた。不確かさだけでなく、中間の状態があってもいいのだ。電子の波動としての側面と粒子としての側面は互いに補完しあっており、両者が合わさったものが電子そのものなのである。このように、電子は相補関係にある対(ペア)――波動と粒子、位置と運動量――からできている。
ボーアは相補性を論じた論文の写しをパウリに送り、校訂と忌憚のない批評を求めた。細かな点でいくつかコメントを付したことを除けば、パウリはボーアの考え方に全面的な賛意を表わした。
もっとも、相補性という考え方を真剣に受け止めたのは、「哲学」にかなり関心をもっている科学者だけであろう。そしてパウリはその一人であった。「知識を獲得する」ために洋の東西で実践されているさまざまな取り組みにも同様の考えが見られるように、パウリは意識を研究するためのもう一つの手段として相補性に注目するようになった。彼は意識と無意識、合理的なものと不合理なものへの関心に加え、こうした相補的なものを理解するのに物理学をどのように利用できるかにも、ますます大きな関心をもつようになった。
一九二六年の秋、一風変わった二四歳のイギリスの物理学者ポール・ディラックがボーアの研究所にやってきた。すでに原子物理学に重要な寄与をしていたディラックは、同世代の物理学者たちと親交を結ぶのを望んでおり、彼らの論文に注意深く目を通していたが、彼がとりわけつぶさに調べたのは、ハイゼンベルクとパウリの論文であった。
ディラックは内々にではあったが、光と物質は波動と粒子のどちらでもあるのかをめぐって、ボーアとハイゼンベルクのあいだで戦わされていた激しい議論にも関与していた。イギリスに戻った彼は一九二七年に、以前に考案した数学的手法を利用して、波動から粒子、および粒子から波動への変化を解明する決定的な説明を与え、それによって「波動による記述と光量子による記述との完全な調和」をもたらした。ディラックが用いた数学的手法は、究極的には電子と光がどのように相互作用するのかを問題にしていた。彼の手法は、科学者たちが『量子電磁力学』と呼ぶ、まったく新しい学問分野の基礎を築いた。パウリとハイゼンベルクは新たに登場したこの領域を発展させるために、夢中になって研究に取り組んだ。
翌一九二八年、ディラックはきわめて重要な方程式を提示した。それがディラック方程式である。電子が光とどのように相互作用するかを表わすディラック方程式は、相対性理論と矛盾することもなかった。ハイゼンベルクの理論とシュレーディンガーの理論は、相対性理論とあい入れなかっただけでなく、無理やりにでもスピンを取り込まなければならなかったのに対して、ディラック方程式には、ごく自然な帰結としてスピンが現われた。こうして、彼の理論はスピンと相対性理論とのつながりをはっきりさせたのである。
だが、パウリたちは納得できなかった。とりわけ問題だったのは、電子を記述するディラック方程式が負のエネルギーをもつ物体の実在を予測していたことである。当時の物理学者たちは、負のエネルギーをもつ粒子は負の時間と同様、絶対に存在するはずがないと考えていた。ハイゼンベルクはパウリヘの手紙のなかで、ディラック方程式は「現代物理学のもっとも嘆かわしい一部です」とコメントしている。加えて、ディラックの理論はパウリの排他原理については何も解明できなかった。
少し話がそれるが、一九三二年の一月に、ユング邸に一人の科学者が足を踏み入れた。この科学者こそパウリその人である。この時からパウリがユングとの秘密研究で探求しようとした、物理学に関する「数」を巡る旅が始まったのかもしれない。
ユング『タイプ論』のなかで内向的思考タイプについて述べている内容は、下記の通りパウリ自身と驚くほどぴったり重なりあうものであった。
「このタイプの人間の判断は、冷淡でかたくなであり、配慮に欠けているように思われる……自分にとって明らかなことが他の人にも同じように明らかだとはかぎらないことを、自身ではなかなか認めることができない……自分を理解してもらえない相手と出会った場合には、人間が計り知れないほど愚かであることを裏づける、さらなる証拠を集めようとし……子どものような心をもつ人間嫌いの独身主義者になることもある……まわりからは、怒りっぽくて打ち解けず、高慢な人間であるように見え……異性に対して漠然とした恐怖感を抱いている。」
また、パウリはユング邸は訪れる前に、彼の著書である『タイプ論』の中の次の一節に三本の縦線を引いている。
「ペルソナが知的である場合、魂は決まって感傷的で……非常に女らしい女性には男性的な魂があり、非常に男らしい男性には女性的な魂がある。この対立状況が生まれるもとは、一例をあげれば、男性は何事においても完全に男性的というわけではなく、女性の特質のいくつかも併せもっているという事実にある」
パウリは一九三四年に、ディラック方程式に代わる新たな方程式を見つけるための研究に着手した。彼とともにこの研究に取り組んだのは、助手を務めていたヴィクター・ヴァイスコップである。二人が提示した方程式は、ディラック方程式に見られる特性の大半を備えており、相対性理論とも整合した。しかし、ディラック方程式が単位量の二分の一のスピンをもつ粒子(電子)を扱っていたのに対して、パウリとヴァイスコップの方程式は、当時まだ検出されていなかったスピンがゼロの粒子についての方程式であった。ところがスピンを取り込むと、彼らの方程式はもはや相対性理論とは両立しなくなってしまった。
なぜ両立しないのだろうか。方程式をあれこれいじくり回していたパウリは、まったく新しい重要な事実に気づいた。それは、スピンがゼロの粒子は、単位量の半奇数倍のスピンをもつ粒子とは根本的に異なる、というものであった。単位量の半奇数倍(すなわち1/2倍、3/2倍など)のスピンをもつ粒子は、イタリアの物理学者エンリコ・フェルミの名にちなんでフェルミオンないしはフェルミ粒子と呼ばれている。フェルミオンはフェルミ統計(一九二六年にフェルミとディラックが発見)にしたがうが、これは、フェルミオンあるいは同種のフェルミオンの集団の量子力学的状態を表わす波動関数が、非対称性を示すことを意味している(量子力学では、「統計」という言葉は、集団の波動関数が粒子の位置とスピンの交換に対して対称か非対称かを表わすのに使われる場合がある)。
当時知られていたフェルミオンは電子、中性子、ニュートリノ、陽子だけであった【ただし、ニュートリノについては、その存在は確実視されていたとはいえ直接証明されてはいなかった】。フェルミオンに対して、単位量の整数倍(0倍、1倍、2倍など)のスピンをもつ粒子のほうは、インドの物理学者サティエンドラ・ボースの名にちなんでボソンまたはボース粒子と呼ばれ、ボース統計(一九二四年にボースとアインシュタインが発見)にしたがう。
ボソンの場合は、系の波動関数は粒子の位置とスピンを入れ替えても不変に保たれる。つまりボソンの系の波動関数は対称なのである。言いかえれば、フェルミオンとボソンの二組の粒子は、対称性に関して異なる性質をもつということである。パウリはこうしたことをもとに、排他原理は単位量の半奇数倍のスピンをもつ粒子には適用できるが、単位量の整数倍のスピンをもつ粒子には適用できないという結論に到達した。
とはいえ、そう結論する明白な根拠は何もなかった。自然はそう言っている、としか言いようがない。波動関数には数学を超える何かがある。物理学者たちは今度は、あらゆる値のスピンをもつ粒子について、その波動関数の特性を探る研究に乗りだした。それに伴う難解な数学を相手にするのは、まさにパウリの好むところであった。
それから六年後の一九四〇年、彼は波動関数とスピンとの関係を考察した研究の要点を的確にまとめた上で、それを一般的な形に拡張した。ディラック方程式や自身の方程式などの特定の波動方程式を使わず、波動関数の数学的特性を利用して、相対性理論、スピン、統計、排他原理を適用した場合に波動関数がどのような挙動を示すかを探ったのである。彼はひたすら数学のなかを突き進み、きわめて重要な結論を導き出した。その結論とは、排他原理は、単位量の整数倍のスピンをもつ粒子(整数のスピンをもつ粒子)を扱う相対論的理論には適用できないが、それでも、この原理は半整数のスピンをもつ粒子を扱う理論には絶対に欠かすことができない、というものであった。
彼は論文の最後に、「スピンと統計を関連づけることは、特殊相対性理論のきわめて重要な応用の一つである」と述べている。何年にもわたってスピン、統計、相対性理論のあいだの関係を明らかにしようとしてきた彼は、いまようやく、その目標を達成した。簡潔でありながらも、数学を使って論理的に厳密に主張を述べたこの論文には、彼の本領がいかんなく発揮されている。多くの物理学者が、この論文をパウリの最高傑作と見なした。
排他原理とスピンの概念――さらに、量子数は三つではなく四つであること――に思い至ってから二年近くの歳月を経て、ついにパウリは、自身が成しとげた最初の大きな発見である排他原理に秘められた重要な意味の一端を何とか突き止めることができた。排他原理の発見当初から、物理学者たちはこの原理によって元素の周期表を説明できることを理解した。今度は、排他原理は半奇数のスピンをもつあらゆる粒子の振る舞いを調べるのには利用できるが、それ以外の粒子にはまったく関係がないことがわかったのである。









