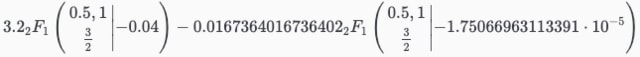Julia: sin33°、cos33°、tan33°はどんな数？ 再び

sin33°、cos33°、tan33°はどんな数？
https://p-suugaku.blogspot.com/2022/01/sin33cos33tan33.html

については，

Julia/SymPy: sin(33°)，cos(33°)，tan(33°)
https://blog.goo.ne.jp/r-de-r/e/5aa2b18080d95d0e6b9213493d8bceb9

に，すでに書いたけど，tan(33°) の simplify をやった結果も書いておこう。

元ページには写し間違いとは思うが，間違いがある。

手入力は間違いの元，コピペするに限る。検算すればいいだけの話です。

using SymPy
@syms a

##### sin(33°)

sind(33) # 0.5446390350150271

s1 = sind(Sym(33)) |> simplify |> together

s2 = s1(√(5-√Sym(5))=>a)

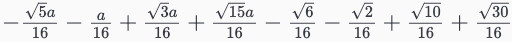
s3 = s2.coeff(a, 1) |> together |> numer

s4 = 2√(expand(s3^2 * (5-√Sym(5)))/4)/16 + s2.coeff(a, 0)
s4.evalf() # 0.544639035015027
sind(33)   # 0.5446390350150271
s4 |> print
# -sqrt(6)/16 - sqrt(2)/16 + sqrt(10)/16 +
# sqrt(-10*sqrt(3) - 2*sqrt(15) + 4*sqrt(5) + 20)/8 + sqrt(30)/16

(a) 式の3行目10√10 は 10√3
(√6 - √2)/4 * √(10 + 2√5)/4 + (√6 + √2)/4 * (√5 - 1)/4        # 0.544639035015027
√2*((√3 - 1) * √(10 + 2√5) + (√3 + 1) * (√5 - 1))/16          # 0.5446390350150271
# (2*√(20 - 10√10 +4√5  - 2√15) - √2 - √6 + √10 + √30) / 16   # error!
  (2*√(20 - 10√3  + 4√5 - 2√15) - √2 - √6 + √10 + √30) / 16   # 0.5446390350150272

##### cos(33°)

cosd(33) # 0.838670567945424

c1 = cosd(Sym(33)) |> simplify |> together

c2 = c1(√(5-√Sym(5))=>a)

c3 = c2.coeff(a, 1) |> together |> numer

c4 = 2√(expand(c3^2 * (5-√Sym(5)))/4)/16 + c2.coeff(a, 0)

c4.evalf() # 0.838670567945424
cosd(33) # 0.838670567945424
c4 |> print
# -sqrt(30)/16 - sqrt(2)/16 + sqrt(6)/16 + sqrt(10)/16 +
#  sqrt(2*sqrt(15) + 4*sqrt(5) + 10*sqrt(3) + 20)/8

(b) 式の3行目の 10√10 も 10√3 の間違い
(√6 + √2)/4 * √(10 + 2√5)/4 - (√6 - √2)/4 * (√5 - 1)/4      # 0.8386705679454239
√2*((√3 + 1) * √(10 + 2√5) - (√3 - 1) * (√5 - 1))/16        # 0.838670567945424
# (2*√(20 + 10√10 + 4√5 + 2√15) - √2 + √6 + √10 - √30) / 16 # error!
  (2*√(20 + 10√3  + 4√5 + 2√15) - √2 + √6 + √10 - √30) / 16 # 0.8386705679454238

##### tan(33°)

tand(33) # 0.6494075931975105

t1 = tand(Sym(33)) |> simplify |> together

numerator = numer(t1)

denominator = denom(t1)

denominator0 = denominator(√Sym(6)=>-√Sym(6))

denominator2 = expand(denominator * denominator0)

denominator00 = denominator2(8=>-8)

denominator = expand(denominator2 * denominator00) # 256
numerator = expand(numerator * denominator0 * denominator00)

t2 = numerator / denominator |> simplify

t3 = -√(50 - 10√Sym(5))/2 - √(10 - 2√Sym(5)) + √(150 - 30√Sym(5))/4 + 3√(30 - 6√Sym(5))/4t3.evalf()

t4 = - √Sym(5) - 2 + √Sym(15)/2 + 3√Sym(3)/2

y = (5 - √Sym(5))*((-2√Sym(10) + √Sym(30) - 4√Sym(2) + 3√Sym(6))/4)^2

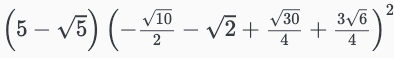
expand(y*4)

t6 = √expand(y*4)/2 + t4

t6.evalf() # 0.649407593197511

tand(33) # 0.6494075931975105

Julia: プログラムを速くするための定石--その6

Julia: プログラムを速くするための定石
https://blog.goo.ne.jp/r-de-r/e/2e21bccd94b2f24cdbc2b54030b13a1a

Julia: プログラムを速くするための定石--その2
https://blog.goo.ne.jp/r-de-r/e/4a815e35e7364368ed963e75a966b595

Julia: プログラムを速くするための定石--その3
https://blog.goo.ne.jp/r-de-r/e/bb84137b4936fb4ab5e76a3cbd7ce9e5

Julia: プログラムを速くするための定石--その4
https://blog.goo.ne.jp/r-de-r/e/6b538afd6188153bf5e7db614b67f5e5

Julia: プログラムを速くするための定石--その5 の続きである
https://blog.goo.ne.jp/r-de-r/e/2aad94a1df626356ffab159eb16f00f4

で，今回は，

素数の末尾の桁の続き
http://commutative.world.coocan.jp/blog5/2021/12/post-507.html

である。

速くするための定石（関数化する，ファイルは読まないなど）は同じである。
しかしその他に，このプログラムにおいては，速くするというのとは直接関係がないが，繰り返し記述を避けるということを挙げておく。
カウントのために n11~n99 という16個の変数を使っているが，その後の 16 段にわたる if-elseif での記述や 16 行の print/println を見ると，二次元配列を使うのがまっとうだとわかる。

なにはともあれ，元のプログラムの出力結果と計算時間は以下のとおりである。

11: 21423878,13: 33479893,17: 33692895,19: 25164853
31: 27517671,33: 20741925,37: 31818060,39: 33687968
71: 28959412,73: 30589282,77: 20731084,79: 33484260
91: 35860558,93: 28954524,97: 27521999,99: 21424245

177.184738 seconds (1.82 G allocations: 33.924 GiB, 1.34% gc time, 0.02% compilation time)

元の 68 行のプログラムを，以下の 16 行のプログラムのように書き換えた。
短いプログラムはそれだけで，見通しが良い。

using Primes, Printf
function g(n=10^10)
  cnt = zeros(Int, 9, 9)
  a = 2
  for p in primes(3, n)
    b = p % 10
    cnt[a, b] += 1
    a = b
  end
  for i in [1, 3, 7, 9]
    for j in [1, 3, 7, 9]
      @printf("  %d%d: %7d", i, j, cnt[i, j])
    end
    println()
  end
end

@time g(10^10)

結果は以下のとおり。

11: 21423878  13: 33479893  17: 33692895  19: 25164853
31: 27517671  33: 20741925  37: 31818060  39: 33687968
71: 28959412  73: 30589282  77: 20731084  79: 33484260
91: 35860558  93: 28954524  97: 27521999  99: 21424245

26.982763 seconds (334 allocations: 5.885 GiB, 0.56% gc time)

177.184738/26.982763 ≒ 6.5 倍速

なお，上の結果は，10^10 までの素数(最初の 455052511 個の素数)，元ページに書かれている結果は最初の 10^8 個の素数についての結果。

@time g(2038074743)

11: 4623041  13: 7429438  17: 7504612  19: 5442344
31: 6010981  33: 4442561  37: 7043695  39: 7502896
71: 6373982  73: 6755195  77: 4439355  79: 7431870
91: 7991431  93: 6372940  97: 6012739  99: 4622916

4.755174 seconds (334 allocations: 1.254 GiB, 3.46% gc time)

Julia: プログラムを速くするための定石--その5

Julia: プログラムを速くするための定石
https://blog.goo.ne.jp/r-de-r/e/2e21bccd94b2f24cdbc2b54030b13a1a

Julia: プログラムを速くするための定石--その2
https://blog.goo.ne.jp/r-de-r/e/4a815e35e7364368ed963e75a966b595

Julia: プログラムを速くするための定石--その3
https://blog.goo.ne.jp/r-de-r/e/bb84137b4936fb4ab5e76a3cbd7ce9e5

Julia: プログラムを速くするための定石--その4 の続きである
https://blog.goo.ne.jp/r-de-r/e/6b538afd6188153bf5e7db614b67f5e5

で，

ボレル予想
http://commutative.world.coocan.jp/blog5/2021/12/post-497.html

√2 の2進表示中の 0 と 1 の個数の勘定

元のプログラムの改善点は，関数にする，global を使わない，BigFloat の使い方，ビット 0/1 は両方数えなくてもよい，Int(floor(X)) より floor(Int, X) のほうが速い，何より，必要な桁数（precision）を正しく見積もる。

元のプログラムの実行結果は，

number of 0s: 500119, number of 1s: 499882
407.799036 seconds (9.55 M allocations: 4.550 TiB, 23.94% gc time)

書き換えたプログラムは以下の通り。

function f(n=1000000; precision=10000000)
  setprecision(precision)
  X = sqrt(big"2") - 1 # 直接求める
  NO = 1 # considering "1...."
  for i=1:n
    X *= 2
    floor(Int, X) == 1 && (NO += 1; X -= 1) # 整数部が 1, Int(floor(X)) より速い
  end
  NZ = n + 1 - NO # NZ は数えなくてよい
  println("number of 0s: $NZ, number of 1s: $NO")
end

@time f(1000000, precision=1000000)

書き換えの経過

このプログラムは，関数化してもたいして速くならない
number of 0s: 500119, number of 1s: 499882
402.086354 seconds (8.55 M allocations: 4.550 TiB, 23.34% gc time)

1 だけを数えれば，計算時間はほぼ半分になると期待される（実際は半分より長い）
number of 0s: 9500119, number of 1s: 499882
271.447004 seconds (7.05 M allocations: 3.413 TiB, 25.05% gc time)

X -= floor(X) するのは無駄
floor(Int, X) は Int(floor(X)) より速い
number of 0s: 500119, number of 1s: 499882
184.315439 seconds (5.05 M allocations: 2.276 TiB, 29.69% gc time)

X は直接 sqrt(big"2") - 1 でよい
for i=1:1000000 で回しているのは，2進数での桁数。よって，precision でも 1000000 で十分(n より多めにとっておく)
number of 0s: 500119, number of 1s: 499882
 18.305939 seconds (5.01 M allocations: 233.246 GiB, 24.00% gc time)

これにより，
402.086354 / 18.305939 = 21.96480355364453 倍速

円周率 π の2進表示中の 0 と 1 の個数の勘定

function g(n=1000000; precision=10000000)
  setprecision(precision)
  X = big(π) - 3 # 直接求める
  NO = 2 # considering "11...."
  for i=1:n
    X *= 2
    floor(Int, X) == 1 && (NO += 1; X -= 1) # 整数部が 1, Int(floor(X)) より速い
  end
  NZ = n + 2 - NO # NZ は数えなくてよい
  println("number of 0s: $NZ, number of 1s: $NO")
end

@time g(1000000, precision=1100000)

元のプログラムは π をファイルで読んでいるので遅いだろう（ファイルを用意できないので再試できない）。
precision は √2 のときより少し多くしておく。

実行結果

number of 0s: 500279, number of 1s: 499723
 21.048134 seconds (5.00 M allocations: 256.281 GiB, 23.65% gc time)

 

Julia: プログラムを速くするための定石--その4

Julia: プログラムを速くするための定石
https://blog.goo.ne.jp/r-de-r/e/2e21bccd94b2f24cdbc2b54030b13a1a

Julia: プログラムを速くするための定石--その2
https://blog.goo.ne.jp/r-de-r/e/4a815e35e7364368ed963e75a966b595

Julia: プログラムを速くするための定石--その3 の続きである
https://blog.goo.ne.jp/r-de-r/e/bb84137b4936fb4ab5e76a3cbd7ce9e5

この記事では，適切な手法を選択する必要性を述べる。

リストがソートされている場合，逐次探索ではなく，二分探索すべし。

さて，

素数の末尾の桁の多連星
http://commutative.world.coocan.jp/blog5/2022/01/post-510.html

まず，四連星

元プログラムを以下のように書き換えた。

using Primes

function g(n)
  cnt = zeros(Int, 9)
  a, b, c = 2, 3, 5
  for p in primes(7, n)
     d = p%10
     a == b == c == d && (cnt[a] += 1)
     a, b, c = b, c, d
  end
  for i in [1, 3, 7, 9]
    println("$i$i$i$i: $(cnt[i])")
  end
end

@time g(10^10)

元のプログラム

1111: 592917
3333: 584632
7777: 584595
9999: 593299
177.256503 seconds (1.37 G allocations: 27.177 GiB, 0.76% gc time, 0.00% compilation time)

改良後

1111: 592917
3333: 584632
7777: 584595
9999: 593299
 27.439484 seconds (18.69 k allocations: 5.886 GiB, 0.30% gc time, 0.07% compilation time)

6.5 倍ほど速くなった。

 

次に重連星を探すが，

元記事に「プログラムは、四連星の場合の自明な変更でいいので、ここには示さない。」と書いてあるが，かなり面倒なことになるだろう。
上のプログラムならば，変更は僅かである。

using Primes

function g11(n)
  cnt = zeros(Int, 9)
  a, b, c, d, e, f, g, h, i, j = 2, 3, 5, 7, 1, 3, 7, 9, 3, 9
  prime_list = primes(31, n)
  for p in prime_list
      k = p%10
      if a == b == c == d == e == f == g == h == i == j == k
        cnt[a] += 1
        pos = searchsortedfirst(prime_list, p)
        println(prime_list[pos-10:pos])
      end
      a, b, c, d, e, f, g, h, i, j = b, c, d, e, f, g, h, i, j, k
  end
  for i in [1, 3, 7, 9]
    println("$i$i$i$i$i$i$i$i$i$i$i: $(cnt[i])")
  end
end

@time g11(10^10)

見つかった11連星を表示しないバージョン

11111111111: 0
33333333333: 1
77777777777: 2
99999999999: 0
 29.098075 seconds (201 allocations: 5.885 GiB, 0.51% gc time)

見つかった11連星を表示するバージョン

ほとんど追加時間なく処理を終える。
なお，searchsortedfirst() は二分探索するので速いのだが，もし indexin() などを使うと，大変なことになるので注意。

 [452942827, 452942837, 452942857, 452942927, 452942947, 452942977, 452943047, 452943097, 452943107, 452943137, 452943157]
 [2820087797, 2820087817, 2820087847, 2820087917, 2820087947, 2820087967, 2820088067, 2820088097, 2820088127, 2820088147, 2820088157]
 [6879806623, 6879806663, 6879806723, 6879806753, 6879806783, 6879806803, 6879806833, 6879806873, 6879806893, 6879806903, 6879806933]
 11111111111: 0
 33333333333: 1
 77777777777: 2
 99999999999: 0
  29.096040 seconds (1.34 k allocations: 5.885 GiB, 0.55% gc time)

 

Julia: プログラムを速くするための定石--その3

Julia: プログラムを速くするための定石

Julia: プログラムを速くするための定石--その2 の続きである

 

さて，

素数の末尾の桁の三連星

http://commutative.world.coocan.jp/blog5/2021/12/post-504.html

元プログラムは，素数リストをファイルから入力する，プログラムを関数化していないなど，実行速度を上げるためには幾つかの改善が必要である。
実行速度は

157.451095 seconds (1.38 G allocations: 27.355 GiB, 1.26% gc time, 0.00% compilation time)
改良プログラムは

関数化，global を除くことにより，
111: 3615401
333: 3553485
777: 3551409
999: 3614711
 45.741210 seconds (455.21 M allocations: 13.581 GiB, 1.24% gc time, 0.03% compilation time)

ファイルからの入力をやめることにより，
111: 3615401
333: 3553485
777: 3551409
999: 3614711
 29.176872 seconds (125 allocations: 5.885 GiB, 0.02% gc time)

&& の代替処理, a, b, c の効率的な使用, カウント用配列
速度には関係ないが表示を for ループで行うなどで，

111: 3615401
333: 3553485
777: 3551409
999: 3614711
 27.276849 seconds (140 allocations: 5.885 GiB, 0.52% gc time)
最終的には 5.8 倍ほど速くなった。

using Primes
function g(n)
  cnt = zeros(Int, 9)
  a, b = 2, 3
  for p in primes(5, n)
     c = p%10
     a == b == c && (cnt[a] += 1)
     a, b = b, c
  end
  for i in [1,3,7,9]
    println("$i$i$i: $(cnt[i])")
  end
end

@time(g(10^10))

Julia: プログラムを速くするための定石--その2

Julia: プログラムを速くするための定石 の続きである

素数の末尾の桁
http://commutative.world.coocan.jp/blog5/2021/12/post-500.html

10^10 までの素数を検査するのに 133.399550 秒かかるが，そのうちの約半分の 60 秒が素数リストをファイルから入力することで費やされている。

global が使われているが，よほど古いバージョンの Julia が動いていない限りは，不要というより，害悪である。

バージョン 1.4 までは，for ループの内部で外部の変数を参照するときに global の指定が必要だった。

Version 1.4.2 (2020-05-23)
julia> count = 0
0

julia> for i in 1:10
         count += 1
       end
ERROR: UndefVarError: count not defined
Stacktrace:
 [1] top-level scope at ./REPL[2]:2

julia>

julia> for i in 1:10
         global count += 1
       end

julia> count
10

しかし，バージョン 1.5 以降では不要である。

Version 1.5.4 (2021-03-11)

julia> count = 0
0

julia> for i in 1:10
       count += 1
     end

julia> count
10

一般的に global が必要な局面は，ほとんど存在しない。関数の引数にするなど，global を使わないで済ますべきだ。

また，別の記事でも書いたが，プログラムをトップレベルに書くのは良くない。どんなプログラムでも，関数にすべきである。

元のプログラムでは，

upto 10^9
last digit = 1: 12711386
last digit = 3: 12712499
last digit = 7: 12712314
last digit = 9: 12711333
 15.177027 seconds (254.25 M allocations: 4.548 GiB, 2.37% gc time)

upto 10^10
last digit = 1: 113761519
last digit = 3: 113765625
last digit = 7: 113764039
last digit = 9: 113761326
133.399550 seconds (2.28 G allocations: 40.703 GiB, 1.33% gc time)

である。

後に示すようにプログラムを書き換えると，次のように，ほぼ 5 倍速くなる。。

upto 10^9
last digit = 1: 12711386
last digit = 3: 12712499
last digit = 7: 12712314
last digit = 9: 12711333
  2.227844 seconds (115 allocations: 643.507 MiB, 0.86% gc time)

upto 10^10
last digit = 1: 113761519
last digit = 3: 113765625
last digit = 7: 113764039
last digit = 9: 113761326
 28.000456 seconds (119 allocations: 5.885 GiB, 0.04% gc time)

 

なお，10^8 までの結果で，元のプログラムでは
last digit = 7: 1440496
になっているが，
last digit = 7: 1440495
ではないだろうか?

using Primes
function g2(n=10^8)
  cnt = zeros(Int, 9)
  prime_list = primes(2, n)
  for p in prime_list
    cnt[p%10] += 1
  end
  println("last digit = 1: $(cnt[1])")
  println("last digit = 3: $(cnt[3])")
  println("last digit = 7: $(cnt[7])")
  println("last digit = 9: $(cnt[9])")
end

Julia: プログラムを速くするための定石

弱いゴールドバッハ予想の計算
http://commutative.world.coocan.jp/blog5/cat122/

Julia プログラムを速くするために何をすべきかの例を示すための素材として取り上げる。
元のプログラムは，上のリンクをクリック。

冒頭 12 行は，素数リストをファイルから詠み込んでいる。
しかしこれは，Using Primes; list = primes(2, prime(1000)) とすれば簡単である（時間はかからない）。使えるものは何でも使おう。

さて，元のプログラムはトップレベルに書かれているが，Julia のプログラムを速くするための定石は，「どんなに短くて，一回しか使わないプログラムでも関数にする」ということである。
関数にするだけで，元のプログラムが 40 秒ほどかかっているのが 0.4 秒と，100 倍速くなる。なお，結果の出力はコメントアウトし，条件を満たす個数のみを勘定するようにしている。

次いで，結果のチェック時に a <= b && b <= c をしているが，素数リストの添字 a, b, c のループの開始値を変えれば，ループ回数も減らせるし，このチェック自体不要になる。
この最適化によって，実行時間は 0.075 秒ほどになる。

k の計算に while を使っているが，これと同じことを 1 行で行う。
この最適化は，計算時間にはあまり効果を持たない。

最後に，3 重の for ループで，無駄なループをしないようにする（それまでの和がすでに r を超えれば，それ以降のループは不要）。
この最適化により，実行時間は 0.025 秒ほどになる。

結果，元のプログラムより 1500 倍ほど速くなった。39.674786 / 0.025536 ≒ 1553 

なお，入出力は通常の計算より 3 桁ほどの処理時間を要するので，結果を出力し，出力時間も含めた合計処理時間にはほとんど変化はないというような場合もある。

参考までに，以下に，書き換えたプログラムを示しておく。

function f(n=1000)
  list = primes(2, prime(n));
  # max = i-1
  num = 0
  for r = 7:2:n+1
    k = sum(list .<= r) + 1
    for a = 1:k
      list[a] >= r && break
      for b = a:k
        list[a] + list[b] >= r && break
        for c = b:k
          t = list[a] + list[b] + list[c]
          t > r  && break
          if t == r
            num += 1
            # print("$r = ")
            # print(list[a])
            # print("+")
            # print(list[b])
            # print("+")
            # println(list[c])
          end
        end
      end
    end
  end
  println("num = $num")
end

@time f()

実行時間の変化

関数にする

num = 198418
  0.407057 seconds (1.19 k allocations: 29.109 KiB)
  39.674786 / 0.407057 # 97.4673964579899 倍速くなった

b, c の初期値を a, b にする

num = 198418
  0.074374 seconds (1.19 k allocations: 29.109 KiB)

k の計算に while を使わない

num = 198418
  0.065854 seconds (2.68 k allocations: 2.171 MiB)

a, b, c の for loop で無駄なループをしない（break する）

num = 198418
  0.025536 seconds (2.68 k allocations: 2.172 MiB)
  39.674786 / 0.025536 # 1553.6805294486214 倍速くなった

Julia: 長精度計算するときの注意事項

Juliaによる累乗根の計算
http://commutative.world.coocan.jp/blog5/2021/04/julia-9.html

setprecision(100)
x = BigInt(2)
T = BigFloat(0.2)
x = x^T
println("2^0.2 = $x")
x = x^5
println("(2^0.2)^5 = $x")

の結果が

2^0.2 = 1.1486983549970350156384116963047
(2^0.2)^5 = 2.0000000000000000769547959311696だったので，x と T の定義を以下のように

x = BigInt(2)
T = one(BigInt)
T /= 5して

2^(1/5) = 1.1486983549970350067986269467779
(2^(1/5))^5 = 2.0が得られたとして，

> JuliaのBigFloatの計算において、多倍長浮動小数点数の指数は、可能な限り、BigInt/BigIntの分数として与えるべきであり、下手にそれを割り算して多倍長浮動小数点数にしてしまわない方がいいということである。

> なぜそうなのかと問うても仕方ない。それが(現バージョンの)Juliaの仕様ということである。

対応法としては間違いがないが，「BigInt/BigIntの分数として与えるべき」というのは不正確である。

要するに，長精度計算をする場合でも，BigFloat(0.2) は「64bit 浮動小数点数においては不正確な 0.2 を長精度で表しただけということだ。これを避けるには「BigInt/BigIntの分数として与える」のも正しいが，いつも整数の分数として与えることができるとは限らないこともある。そのような場合には， BigFloat の引数を文字列にするのである。上の例だと BigFloat("0.2") そうすれば，長精度の 0.2 が得られるのだ。big"0.2" でもよい（カッコを付けてはいけないので注意）。

BigFloat(0.2)    # 0.20000000000000001110223024625157
BigFloat("0.2")　# 0.20000000000000000000000000000004
big"0.2"         # 0.20000000000000000000000000000004

Julia/SymPy: 数値代入法による係数の決定

数学検定の準１級１次に出題された「数値代入法」の問題

https://existence-scholar.com/modules/d3diary/index.php?page=detail&bid=2140

using SymPy
@syms a b c d x

左辺

l = 9/(x-1)^2/(x+2)^2

分数の和として表示(apart)

l2 = l |> apart

もうこれで，答えは出た。
l2 の係数を取り出す。

l2.coeff(1/(x-1))   |> print # -2/3 ... a
l2.coeff(1/(x-1)^2) |> print # 1    ... b
l2.coeff(1/(x+2))   |> print # 2/3  ... c
l2.coeff(1/(x+2)^2) |> print # 1    ... d

このやり方は，係数比較法というのだったかな。

別のやりかたの数値代入法は，右辺 a, b, c, d を未知数として

r = a/(x-1) + b/(x-1)^2 + c/(x+2) +d/(x+2)^2

l, r 式の x に 4 通りの値を与え，連立方程式を構成する。

eq1 = Eq(l(x=>2), r(x=>2))
eq2 = Eq(l(x=>3), r(x=>3))
eq3 = Eq(l(x=>4), r(x=>4))
eq4 = Eq(l(x=>5), r(x=>5))

eq1 |> print # Eq(9/16, a + b + c/4 + d/16)
eq2 |> print # Eq(9/100, a/2 + b/4 + c/5 + d/25)
eq3 |> print # Eq(1/36, a/3 + b/9 + c/6 + d/36)
eq4 |> print # Eq(9/784, a/4 + b/16 + c/7 + d/49)

連立方程式を解く

solve([eq1, eq2, eq3, eq4], [a, b, c, d])

結果

Dict{Any, Any} with 4 entries:
  a => -2/3
  d => 1
  c => 2/3
  b => 1

連立方程式を解く別法

係数行列（1//2 などは分数）

A = [1//1 1//1 1//4 1//16
     1//2 1//4 1//5 1//25
     1//3 1//9 1//6 1//36
     1//4 1//16 1//7 1//49]

右辺

constant = [9//16, 9//100, 1//36, 9//784]

A * [a, b, c, d] = constant を解けば解が求められる。

A \ constant # 逆行列を使わない Julia での記法

解（a, b, c, d の順）

4-element Vector{Rational{Int64}}:
 -2//3
  1//1
  2//3
  1//1

左辺から右辺を引くと 0 になることを確認

l - r(a=>-2//3, b=>1, c=>2//3, d=>1) |> simplify |> print # 0

Atkin の篩と，チューンナップした Eratosthenes の篩 速度はほぼ同等！！

タイトルどおり。

エラトステネスの篩も，さらなるチューニングはあるが，まあ程々で。
C で書いたプログラムをコールすれば結果は変わる。
Julia の primes は atkin の篩によるものらしいが，速い（コンパイラ言語のプログラムを読んでいるのだろう）。

Julia の Primes.primes による場合

using Primes
@time p = primes(10^9); # 2.205441 seconds

アトキンの篩

#=
The MIT License (MIT)
    Copyright (c) 2022/01/09 r-de-r
    Permission is hereby granted, free of charge, to any person obtaining a copy
    of this software and associated documentation files (the "Software"), to deal
    in the Software without restriction, including without limitation the rights
    to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
    copies of the Software, and to permit persons to whom the Software is
    furnished to do so, subject to the following conditions:
    The above copyright notice and this permission notice shall be included in all
    copies or substantial portions of the Software.
    THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
    IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
    FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
    AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
    LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
    OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
    SOFTWARE.
=#

function Atkin(limit=10^6)
    """ n 以下の素数をアトキンの篩で生成 """
    sqrt_limit = isqrt(limit)
    isprime = falses(limit)
    for z in [1, 5]
        for y in z:6:sqrt_limit
            y² = y*y
            max_x = floor(Int, sqrt((limit - y²) / 4))
            for i in 1:max_x
                n = 4i*i + y²
                isprime[n] = !isprime[n]
            end
            x = y + 1
            max_x = floor(Int, sqrt((limit + y²) / 3))
            if x <= max_x
                for i in x:2:max_x
                    n = 3i*i - y²
                    isprime[n] = !isprime[n]
                end
            end
        end
    end
    for z in [2, 4]
        for y in z:6:sqrt_limit
            y² = y*y
            max_x = floor(Int, sqrt((limit - y²) / 3))
            for i in 1:2:max_x
                n = 3i*i + y²
                isprime[n] = !isprime[n]
            end
            x = y + 1
            max_x = floor(Int, sqrt((limit + y²) / 3))
            if x <= max_x
                for i in x:2:max_x
                    n = 3i*i - y²
                    isprime[n] = !isprime[n]
                end
            end
        end
    end
    for y in 3:6:sqrt_limit
        y² = y*y
        for x in 1:2
            max_x = floor(Int, sqrt((limit - y²) / 4))
            for i in x:3:max_x
                n = 4i*i + y²
                isprime[n] = !isprime[n]
            end
        end
    end
    for n in 5:2:sqrt_limit
        if isprime[n]
            for i in n*n:n*n:limit
                isprime[i] = false
            end
        end
    end
    isprime[2] = isprime[3] = true
    (1:limit)[isprime]
end

@time a2 = Atkin(10^9); # 3.080654 seconds

エラトステネスの篩

#=
The MIT License (MIT)
    Copyright (c) 2022/01/09 r-de-r
    Permission is hereby granted, free of charge, to any person obtaining a copy
    of this software and associated documentation files (the "Software"), to deal
    in the Software without restriction, including without limitation the rights
    to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
    copies of the Software, and to permit persons to whom the Software is
    furnished to do so, subject to the following conditions:
    The above copyright notice and this permission notice shall be included in all
    copies or substantial portions of the Software.
    THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
    IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
    FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
    AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
    LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
    OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
    SOFTWARE.
=#

# https://qiita.com/peria/items/54499b9ce9d5c1e93e5a を参考に

""" 偶数は対象としないバージョン """
function Eratosthenes(n)
    tbl = trues(ceil(Int, n / 2))
    tbl[1] = false
    sqrt_x = isqrt(n)+1
    sqrt_xi = floor(Int, sqrt_x / 2)
    for i in 2:sqrt_xi
        if tbl[i]
            for mult in 2i * (i - 1) + 1:2i - 1:length(tbl)
                tbl[mult] = false
            end
        end
    end
    pushfirst!(((1:length(tbl))[tbl]) .* 2 .- 1, 2)
end
@time S = Eratosthenes(10^9);  # 3.084727 seconds

 

Julia/SymPy: 無限級数の極限--2

using SymPy
@syms n

summation(1/2^n, (n, 0, oo)) # 2

summation(1/2^n, (n, 1, oo)) # 1

summation(1/((2n+1)*(2n+3)), (n, 1, oo)) # 1/6

summation(1/(n*(n+2)), (n, 1, oo)) # 3/4

summation(1/3^(n-1) - 1/4^n, (n, 1, oo)) # 7/6

summation(1/3^n, (n, 0, oo)) # 3/2

summation(n/(2n+1), (n, 1, oo)) # ∞

summation(1/(n*(n+2)*(n+3)), (n, 1, oo)) # 5/36

summation(cos(n*π/2)/2^n, (n, 1, oo)) |> print  # Sum(cos(pi*n/2)/2^n, (n, 1, oo))
summation(cos(n*π/2)/2^n, (n, 1, 1000)).evalf() # -1/5

summation(π/12 *(1/9)^(n-1), (n, 1, oo)) # 0.294524311274043
3/32*π # 0.2945243112740431

summation(1/(n*(n+1)), (n, 1, oo)) # 1

summation(9*10^(-n), (n, 1, oo)) # 1

summation(1/factorial(n), (n, 0, oo)) # ℯ ネイピアの定数

summation(1/(2n+1)^2, (n, 0, oo)) # π²/8

summation(1/n^2, (n, 1, oo)) # π²/6

summation(1/n^4, (n, 1, oo)) # π⁴/90

summation(1/n^6, (n, 1, oo)) # π⁶/945

summation(1/n^8, (n, 1, oo)) # π⁸/9450

summation(1/n^3, (n, 1, oo)) # ζ(3) = 1.20205690315959

summation(1/n^5, (n, 1, oo)) # ζ(5) = 1.03692775514337

summation(1/n^7, (n, 1, oo)) # ζ(7) = 1.00834927738192

summation(1/n^9, (n, 1, oo)) # ζ(9) = 1.00200839282608

Julia/SymPy: 無限級数の極限

using SymPy

@syms n

1. log(2)

e1 = summation((-1)^(n-1)/n, (n, 1, oo));

e1 |> print # log(2)

e1.evalf()  # 0.693147180559945

2. フーリエ級数

e2 = summation(1/n^2, (n, 1, oo));

e2 |> print # pi^2/6

√(e2 * 6).evalf() # 3.14159265358979

3. グレゴリー・ライプニッツ級数

e3 = summation((-1)^(n-1) / (2n - 1), (n, 1, oo));

e3 |> print  # pi/4

4*e3.evalf() # 3.14159265358979

4. マチンの公式

e4 = summation(16*(-1)^n/(2n+1)*(1/5)^(2n+1) - 4*(-1)^n/(2n+1)*(1/239)^(2n+1), (n, 0, oo))

e4 |> print # 3.2*hyper((0.5, 1), (3/2,), -0.04) - 0.0167364016736402*hyper((0.5, 1), (3/2,), -1.75066963113391e-5)

e4.evalf() # 3.14159265358979

hyper((a, b), (c,), z) は Gauss hypergeometric function の ₂F₁(a, b, c, z)

using HypergeometricFunctions

3.2 * _₂F₁(0.5, 1, 3/2, -0.04) - 0.0167364016736402 * _₂F₁(0.5, 1, 3/2, -1.75066963113391e-5) # 3.1415926535897936

Python の sympy では以下で評価できるが，Julia では（いまのところ）できない。

>>> (3.2*hyper((0.5, 1), (3/2,), -0.04) - 0.0167364016736402*hyper((0.5, 1), (3/2,), -1.75066963113391e-5)).evalf() # 3.14159265358979

5. ラマヌジャン式

e5 = (-1)^n*factorial(4n)*(1123 + 21460n) / 882^(2n+1) / (4^n * factorial(n))^4

4/summation(e5, (n, 0, 0)).evalf() # 3.14158504007124
4/summation(e5, (n, 0, 1)).evalf() # 3.14159265359762
4/summation(e5, (n, 0, 2)).evalf() # 3.14159265358979

収束の速さは目を瞠るものがある。

res = 0
for n = 0:12
    res += (-1)^n * factorial(big(4)n) * (1123 + 21460n) / big(882)^(2n+1) / (4^n * factorial(big(n)))^4
    println("$n $(4/res)")
end
println("pi:", big(pi))

0 3.14158504007123775601068566340160284951024042742653606411398040961709706144257
1 3.141592653597622014268275179202291563387123765940278924800131654234958957780921
2 3.141592653589793229887677088812011582500396626398585829522573327158139832285541
3 3.141592653589793238462653137021443968203070363083330244371464119910981874588252
4 3.141592653589793238462643383268142159665117427792501809002405604153156497729344
5 3.141592653589793238462643383279502897644492229727493144410492231930577371459383
6 3.141592653589793238462643383279502884197153296192775704368162768434095479750287
7 3.141592653589793238462643383279502884197169399394559174859992564888677720166504
8 3.141592653589793238462643383279502884197169399375105797313049395317182201783169
9 3.141592653589793238462643383279502884197169399375105820974973531650835366122329
10 3.141592653589793238462643383279502884197169399375105820974944592272262921459799
11 3.14159265358979323846264338327950288419716939937510582097494459230781645012978
12 3.141592653589793238462643383279502884197169399375105820974944592307816406286094
pi:3.141592653589793238462643383279502884197169399375105820974944592307816406286198

Julia/SymPy: 立方根の方程式

立方根の方程式
https://p-suugaku.blogspot.com/2021/09/rippoukon-houteishiki.html

a = 1/3 のとき，以下の方程式 f(x) = 0 を解けという問題。要するに立方根を含む問題である。
f(x) = (3x+2)^a - (x-2)^a - (x+2)^a

素直に SymPy で解いてみると

using SymPy
@syms a, x

solve((3x+2)^(1/3) - (x-2)^(1/3) - (x+2)^(1/3)) |> float

で，-2.0，2.074772708486752 という 2 つの解が示される（後で示すが，3 つあるはず）。

件の解答例は (2 ± √19) / 3 になっているが，明らかにおかしい。
(2+√19)/3 #  2.119632981180225
(2-√19)/3 # -0.7862996478468913
f((2+√19)/3)(a=>1/3) # −0.0663385359996638
f((2-√19)/3)(a=>1/3) # -1.41493963273732 - 0.60319058562597i
どのようにおかしいか，図にしてみようと plot() で描こうとしたが，x の値によって，上で示した Base で定義した関数 f(x) が計算できない（虚数になる）ので，とりあえず中断。

回答例のどこがおかしいのかな?と追試してみると

>   問の方程式の両辺を 3 乗したものは

　　　　

>   となります。これを整理して

　　　　

としているが，1 行目の右辺が 3 乗されていないのがそもそもの間違い。

正しく計算すれば，5*x^3 + 3*x^2 - 21*x - 14 = 0 となる。

a1 = 5x^3 + 3x^2 - 21x - 14
a2 = solve(a1)
# Sym[-2, 7/10 - 3*sqrt(21)/10, 7/10 + 3*sqrt(21)/10]

a2[2].evalf() # −0.674772708486752
a2[3].evalf() #  2.07477270848675
a1(x=>a2[1]) # 0
a1(x=>a2[2]).evalf() # 3.0 * 10^(-123)
a1(x=>a2[3]).evalf() # -1.0 * 10^(-122)

図に描いてみよう。

plot(a1, xlims=(-2.1, 2.2), labels="")
hline!([0], labels="")
vline!(a2, labels="")

しかし，そもそもは立方根を含む元の式，以下の a3 に代入して 0 になるか確認しなければならない。

a3 = ((3x+2)^a - (x-2)^a - (x+2)^a)(a => 1/3)
a3(x=>a2[1]).evalf() |>print # 0
a3(x=>a2[2]).evalf() |>print # -1.64761112632243 - 0.951248727302079*I
a3(x=>a2[3]).evalf() |>print # -5.73973140632228e-17

つまり，x = −0.674772708486752 の場合には虚数になるので，不適解ということで，
x = -2, 2.07477270848675 の 2 つが解であるということ。
https://www.wolframalpha.com によってもこの 2 つの解が示される。

Julia/SymPy: sin(42°)，cos(42°)，tan(42°)

Julia/SymPy: sin(42°)，cos(42°)，tan(42°)

Julia/SymPy: sin(39°)，cos(39°)，tan(39°)

Julia/SymPy: sin(39°)，cos(39°)，tan(39°)