数学問題

Python では sympy を使う
WolframAlpha の「高等学校 数学」の例題を解いてみる
https://ja.wolframalpha.com/examples/mathematics/koukousugaku/

問題　(1/8)^x ≦ 7(1/2)^x-6をみたす実数ｘを求める

>>> from sympy import *
>>> from sympy.plotting import plot
>>> var('a:z')
(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z)
>>> func1 = (1/8)**x
>>> func2 = 7*(1/2)**x - 6
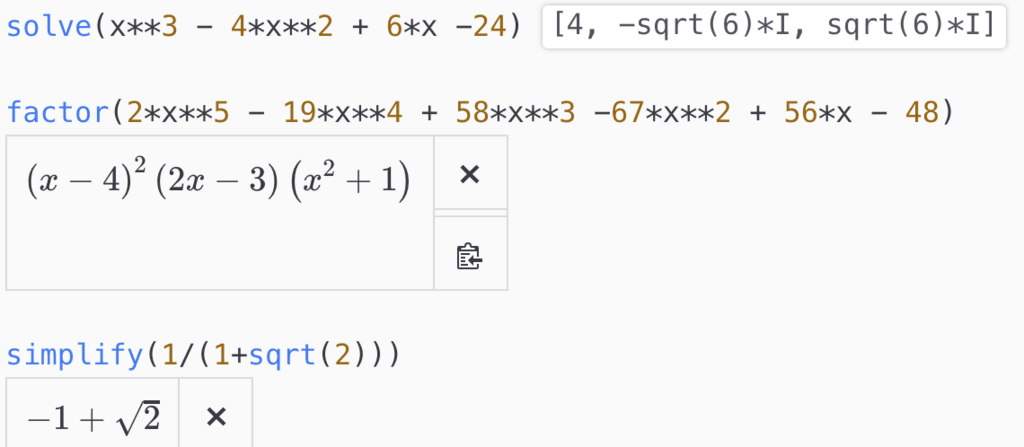
>>> solve(Eq(func1, func2), x)
[-1.00000000000000, 0.0, -1.58496250072116 + 4.53236014182719*I]

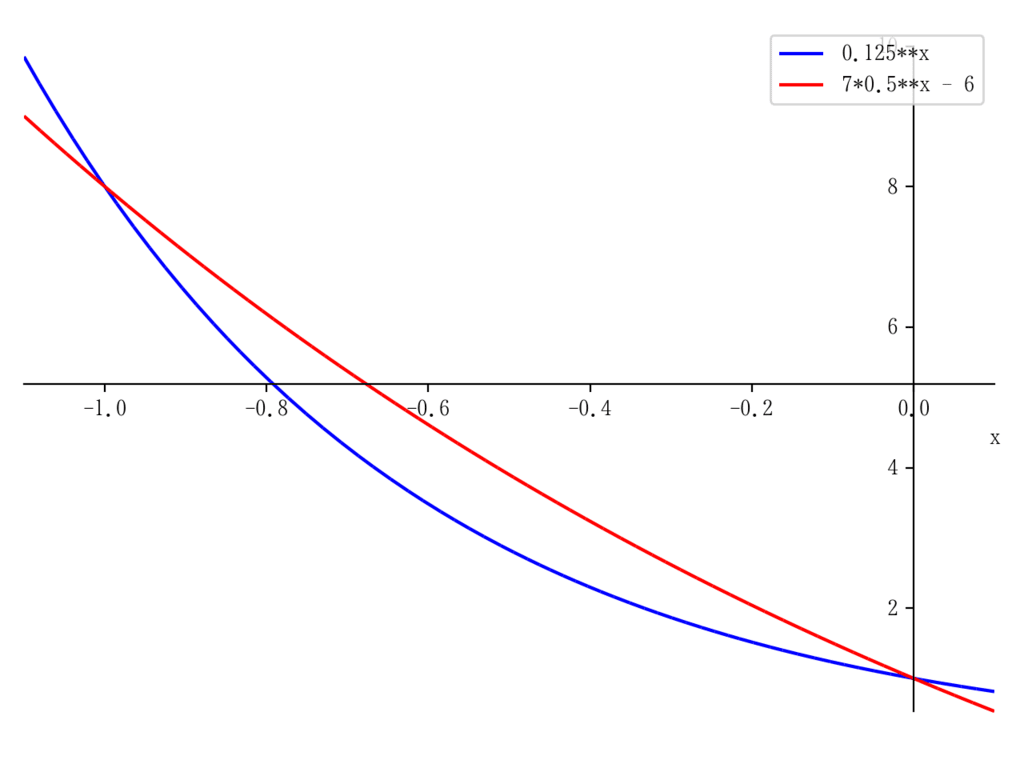
以下のように図を描いて，答えは -1 ≦ x ≦ 0 であることがわかる

>>> p = plot(func1, func2, (x, -1.1, 0.1), legend=True, ylabel='', show=False)
>>> p[0].line_color = 'b'
>>> p[1].line_color = 'r'
>>> p.show()

数式処理-3

Python では sympy を使う
WolframAlpha の「代数」の例題 3 題を解いてみる
https://ja.wolframalpha.com/examples/mathematics/

>>> from sympy import *
>>> var('a:z')
(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z)

問題 1.　方程式を解く　x^3 - 4x^2 + 6x - 24 = 0

>>> solve(x**3 - 4*x**2 + 6*x -24)
[4, -sqrt(6)*I, sqrt(6)*I]

問題 2.　 多項式を因数分解する　2x^5 - 19x^4 + 58x^3 - 67x^2 + 56x - 48

>>> factor(2*x**5 - 19*x**4 + 58*x**3 -67*x**2 + 56*x - 48)
(x - 4)**2*(2*x - 3)*(x**2 + 1)

問題 3.　式を簡約する　1/(1+√2)

>>> simplify(1/(1+sqrt(2)))
-1 + sqrt(2)

数式処理-2

Python では sympy を使う
WolframAlpha の「微積分と解析」の例題 3 題を解いてみる
https://ja.wolframalpha.com/examples/mathematics/

>>> from sympy import *
>>> var('a:z')
(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z)

問題 1.　0 から π の範囲で sin(x)を積分

>>> integrate(sin(x), (x, 0, pi))
2

問題 2.　x^4 * sin(x) の導関数

>>> diff(x**4 * sin(x))
x**4*cos(x) + 4*x**3*sin(x)

問題 3.　常微分方程式 y'' + y = 0 を解く

>>> f = symbols('f', cls=Function)
>>> f(x).diff(x, x) + f(x)
f(x) + Derivative(f(x), (x, 2))
>>> dsolve(f(x).diff(x, x) + f(x), f(x))
Eq(f(x), C1*sin(x) + C2*cos(x))

数式処理

Python では sympy を使う

WolframAlpha の「高等学校 数学」の例題 3 題を解いてみる

https://ja.wolframalpha.com/examples/mathematics/

>>> from sympy import *
>>> var('a:z')
(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z)

問題 1.　y=-x^2+2x+8の頂点の座標

>>> expr = -x**2 + 2*x + 8
>>> a = solve(diff(expr))[0]
>>> b = expr.subs(x, a)
>>> [a, b]
[1, 9]

問題 2.　log(4,x+4)=log(2,2x-7)+log(8,1/(5√5))を解く ※ 第1引数が底

>>> expr = log(x + 4, 4) - log(2 * x - 7, 2) - log(1 / (5 * sqrt(5)), 8)
>>> expr
log(x + 4)/log(4) - log(2*x - 7)/log(2) - log(sqrt(5)/25)/log(8)
>>> solve(expr)
[29/4]

問題 3.　x が 0 に近付くときの (sin x - x)/x^3 の極限

>>> limit((sin(x) - x) / x**3, x, 0)
-1/6

変数のスコープ

ちゃんと理解していないとドツボにはまる（実際嵌まった）

$> cat f1.py
def f1():
  y = x*2
  print("関数の中: x =", x)

x = 10
print("関数を呼ぶ前: x =", x)
f1()
print("関数を呼んだ後: x =", x)

$> python3 f1.py
関数を呼ぶ前: x = 10
関数の中: x = 10
関数を呼んだ後: x = 10

$> cat f2.py
def f2():
  x = x*2
  print("関数の中: x =", x)

x = 10
print("関数を呼ぶ前: x =", x)
f2()
print("関数を呼んだ後: x =", x)

$> python3 f2.py
関数を呼ぶ前: x = 10
Traceback (most recent call last):
  File "f2.py", line 7, in <module>
    f2()
  File "f2.py", line 2, in f2
    x = x*2
UnboundLocalError: local variable 'x' referenced before assignment

$> cat f3.py
def f3(x):
  x = x*2
  print("関数の中: x =", x)

x = 10
print("関数を呼ぶ前: x =", x)
f3(x)
print("関数を呼んだ後: x =", x)

$> python3 f3.py
関数を呼ぶ前: x = 10
関数の中: x = 20
関数を呼んだ後: x = 10

$> cat f4.py
def f4():
  global x
  x = x*2
  print("関数の中: x =", x)

x = 10
print("関数を呼ぶ前: x =", x)
f4()
print("関数を呼んだ後: x =", x)

$> python3 f4.py
関数を呼ぶ前: x = 10
関数の中: x = 20
関数を呼んだ後: x = 20

$> cat f5.py
def f5():
  global x
  x = 100
  print("関数の中: x =", x)

x = 10
print("関数を呼ぶ前: x =", x)
f5()
print("関数を呼んだ後: x =", x)

$> python3 f5.py
関数を呼ぶ前: x = 10
関数の中: x = 100
関数を呼んだ後: x = 100