算額（その2125）

算額（その2125）

一八 大里郡岡部村岡 稲荷社 文化14年(1817)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円5個，外円，弦3本
#Julia, #SymPy, #算額, #和算

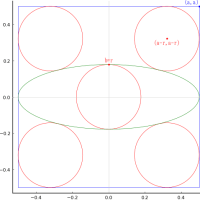
外円の中に 3 本の弦を引き，区画された領域に甲円 1 個，乙円 1 個，丙円 2 個を容れる。甲円の直径が 5 寸，丙円の直径は甲円の直径の 1/3 のとき，乙円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, r1 - R)
乙円の半径と中心座標を r2, (0, R - r2)
丙円の半径と中心座標を r3, (x3, R - 2r2 + r3)
弦と外円の交点座標を (x01, sqrt(R^2 - x01^2)), (x02, sqrt(R^2 - x02^2)), (x03, sqrt(R^2 - x03^2))
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, x01::positive, x02::positive;
R = r1 + r2
r3 = r1/3
eq1 = dist(x01, sqrt(R^2 - x01^2), x02, -sqrt(R^2 - x02^2), 0, R - r2) - r2^2
eq2 = dist(x01, sqrt(R^2 - x01^2), x02, -sqrt(R^2 - x02^2), 0, r1 - R) - r1^2
eq3 = dist(x01, sqrt(R^2 - x01^2), x02, -sqrt(R^2 - x02^2), x3, R - 2r2 + r3) - r3^2
eq4 = x3^2 + (R - 2r2 + r3)^2 - (R - r3)^2;
# res = solve([eq1, eq2, eq3, eq4], (r2, x3, x01, x02))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (r2, x3, x01, x02) = u
   return [
       -r2^2 + (-x01 - (-x01 + x02)*(-x01*(-x01 + x02) + (r1 - sqrt(-x01^2 + (r1 + r2)^2))*(-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2)))/((-x01 + x02)^2 + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))^2))^2 + (r1 - sqrt(-x01^2 + (r1 + r2)^2) - (-x01*(-x01 + x02) + (r1 - sqrt(-x01^2 + (r1 + r2)^2))*(-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2)))*(-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))/((-x01 + x02)^2 + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))^2))^2,  # eq1
       -r1^2 + (-x01 - (-x01 + x02)*(-x01*(-x01 + x02) + (-r2 - sqrt(-x01^2 + (r1 + r2)^2))*(-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2)))/((-x01 + x02)^2 + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))^2))^2 + (-r2 - sqrt(-x01^2 + (r1 + r2)^2) - (-x01*(-x01 + x02) + (-r2 - sqrt(-x01^2 + (r1 + r2)^2))*(-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2)))*(-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))/((-x01 + x02)^2 + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))^2))^2,  # eq2
       -r1^2/9 + (-x01 + x3 - (-x01 + x02)*((-x01 + x02)*(-x01 + x3) + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))*(4*r1/3 - r2 - sqrt(-x01^2 + (r1 + r2)^2)))/((-x01 + x02)^2 + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))^2))^2 + (4*r1/3 - r2 - sqrt(-x01^2 + (r1 + r2)^2) - ((-x01 + x02)*(-x01 + x3) + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))*(4*r1/3 - r2 - sqrt(-x01^2 + (r1 + r2)^2)))*(-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))/((-x01 + x02)^2 + (-sqrt(-x01^2 + (r1 + r2)^2) - sqrt(-x02^2 + (r1 + r2)^2))^2))^2,  # eq3
       x3^2 - (2*r1/3 + r2)^2 + (4*r1/3 - r2)^2,  # eq4
   ]
end;

r1 = 5/2
R = r1 + r2
r3 = r1/3
iniv = BigFloat[1.5, 2.89418, 1.2121, 2.90904]
res = nls(H, ini=iniv)

   ([1.5, 2.581988897471611, 1.2103072956898178, 2.9047375096555625], true)

甲円の直径が 5 寸のとき，乙円の直径は 3 寸である。

すべてのパラメータは以下のとおりである。

   r1 = 2.5;  r2 = 1.5;  r3 = 0.833333;  x3 = 2.58199;  x01 = 1.21031;  x02 = 2.90474;  R = 4

function draw(r1, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = r1/3
   (r2, x3, x01, x02) = res[1]
   R = r1 + r2
   @printf("甲円の直径が %g のとき，乙円の直径は %g である。\n", 2r1, 2r2)
   @printf("r1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  x01 = %g;  x02 = %g;  R = %g\n", r1, r2, r3, x3, x01, x02, R)
   plot()
   circle(0, 0, R)
   circle(0, R - r2, r2, :blue)
   circle(0, r1 - R, r1, :magenta)
   circle2(x3, R - 2r2 + r3, r3, :orange)
   y01 = sqrt(R^2 - x01^2)
   y02 = -sqrt(R^2 - x02^2)
   segment(x01, y01, x02, y02, :green)
   segment(-x01, y01, -x02, y02, :green)
   y03 = R - 2r2
   x03 = sqrt(R^2 - y03^2)
   segment(-x03, y03, x03, y03, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, "R", :red, :center, :bottom, delta=delta/2)
       point(x01, y01, "(x01,y01)", :green, :left, :bottom, delta=delta/2)
       point(x02, y02, "(x02,y02)", :green, :left, delta=-delta/2)
       point(x03, y03, "(x03,y03) ", :green, :right, delta=-delta/2)
       point(0, r1 - R, "甲円:r1,(0,r1-R)", :magenta, :center, delta=-delta/2)
       point(0, R - r2, "乙円:r2,(0,R-r2)", :blue, :center, delta=-delta/2)
       point(x3, R - 2r2 + r3, "丙円:r3\n(x3,R-2r2+r3)", :orange, :center, :bottom, delta=delta/2)
   end  
end;

draw(5/2, true)