算額（その1345）

算額（その1345）

岐阜県垂井町 西法寺 令和6年(2024)
http://www.wasan.jp/gifu/saihoji.html

キーワード：円4個，デカルトの円定理
#Julia, #SymPy, #算額, #和算

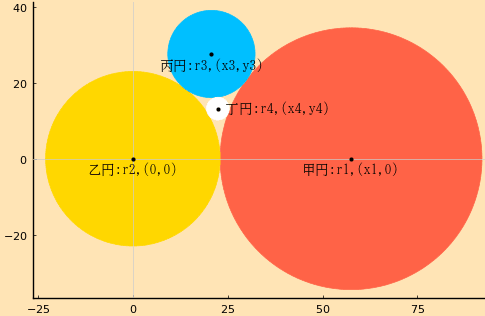
甲円，乙円，丙円が互いに接しており，中央部の隙間に小円が甲円，乙円，丙円に接して入っている。甲円，乙円，丙円の直径がそれぞれ 69 寸，46 寸，23 寸のとき，小円の直径はいかほどか。

1.　デカルトの円定理を用いる場合

甲円，乙円，丙円，小円の半径を r1, r2, r3, r4 とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, r3::positive, r4::positive
(r1, r2, r3) = (69, 46, 23) .//2
eq1 = 1/r1 + 1/r2 + 1/r3 + 2sqrt(1/(r1*r2) + 1/(r2*r3) + 1/(r3*r1)) - 1/r4
solve(eq1, r4)[1] |> println

   3.00000000000000

小円の半径は 3，直径は 6 である。

2.　全てのパラメータを連立方程式で求める場合

甲円の半径と中心座標を r1, (x1, 0); x1 = r1 + r2
乙円の半径と中心座標を r2, (0, 0)
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (x4, y4)
とおき，以下の連立方程式を解く。

using SymPy
@syms r1::positive, x1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive,
     r4::positive, x4::positive, y4::positive;
x1 = r1 + r2
eq1 = (x1 - x4)^2 + y4^2 - (r1 + r4)^2
eq2 = (x1 - x3)^2 + y3^2 - (r1 + r3)^2
eq3 = x3^2 + y3^2 - (r2 + r3)^2
eq4 = x4^2 + y4^2 - (r2 + r4)^2
eq5 = (x3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5], (r4, x3, y3, x4, y4))

SymPy では一度に解くことができないので，まず eq1, eq2, eq3, eq4 を連立させ，x3, y3, x4, y4 を求める。

res = solve([eq1, eq2, eq3, eq4], (x3, y3, x4, y4))[1]

   ((r1*r2 - r1*r3 + r2^2 + r2*r3)/(r1 + r2), 2*sqrt(r1)*sqrt(r2)*sqrt(r3)*sqrt(r1 + r2 + r3)/(r1 + r2), (r1*r2 - r1*r4 + r2^2 + r2*r4)/(r1 + r2), 2*sqrt(r1)*sqrt(r2)*sqrt(r4)*sqrt(r1 + r2 + r4)/(r1 + r2))

得られた解を eq5 に代入し，r4 について解く。

eq15 = eq5(x3 => res[1], y3 => res[2], x4 => res[3], y4 => res[4]);
res2 = solve(eq15, r4)[1];  # 1 of 2

小円の半径 r4 は，甲円，乙円，丙円の r1, r2, r3 の関数で表すことができる（長いが）。

res2 |> println

   (-2*r1^(3/2)*r2^(3/2)*r3^(3/2)*sqrt(r1 + r2 + r3) + r1*r2*r3*(r1*r2 + r1*r3 + r2*r3))/(r1^2*r2^2 - 2*r1^2*r2*r3 + r1^2*r3^2 - 2*r1*r2^2*r3 - 2*r1*r2*r3^2 + r2^2*r3^2)

甲円，乙円，丙円の直径がそれぞれ 69 寸，46 寸，23 寸のとき，小円の直径は 6 寸である。

res2(r1 => 69/2, r2 => 23, r3 => 23/2).evalf() * 2 |> println

   6.00000000000001

全てのパラメータは以下のとおりである。

   r1 = 34.5;  r2 = 23;  r3 = 11.5;  r4 = 3;  x4 = 22.4;  y4 = 13.2;  x1 = 57.5;  x3 = 20.7;  y3 = 27.6

function draw(r1, r2, r3, more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r4 = (-2*r1^(3/2)*r2^(3/2)*r3^(3/2)*sqrt(r1 + r2 + r3) + r1*r2*r3*(r1*r2 + r1*r3 + r2*r3))/(r1^2*r2^2 - 2*r1^2*r2*r3 + r1^2*r3^2 - 2*r1*r2^2*r3 - 2*r1*r2*r3^2 + r2^2*r3^2)
   (x3, y3, x4, y4) = ((r1*r2 - r1*r3 + r2^2 + r2*r3)/(r1 + r2), 2*sqrt(r1)*sqrt(r2)*sqrt(r3)*sqrt(r1 + r2 + r3)/(r1 + r2), (r1*r2 - r1*r4 + r2^2 + r2*r4)/(r1 + r2), 2*sqrt(r1)*sqrt(r2)*sqrt(r4)*sqrt(r1 + r2 + r4)/(r1 + r2))
   x1 = r1 + r2
   @printf("r1 = %g;  r2 = %g;  r3 = %g;  r4 = %g;  x4 = %g;  y4 = %g;  x1 = %g;  x3 = %g;  y3 = %g", r1, r2, r3, r4, x4, y4, x1, x3, y3)
   plot(background_color=:moccasin)
   circlef(x1, 0, r1, :tomato)
   circlef(0, 0, r2, :gold)
   circlef(x3, y3, r3, :deepskyblue)
   circlef(x4, y4, r4, :white)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, 0, "甲円:r1,(x1,0)", :black, :center, delta=-delta)
       point(0, 0, "乙円:r2,(0,0)", :black, :center, delta=-delta)
       point(x3, y3, "丙円:r3,(x3,y3)", :black, :center, delta=-delta)
       point(x4, y4, " 丁円:r4,(x4,y4)", :black, :left, :vcenter)
   end  
end;

draw(69/2, 46/2, 23/2, true)