首都圏直下型地震の予測計算

数日前、新聞社各紙がほぼ一斉に、マグニチュード7クラスの直下型地震が今後4年以内に70％の確率で起きるという予想を報道し、テレビ局もフォローしていました。
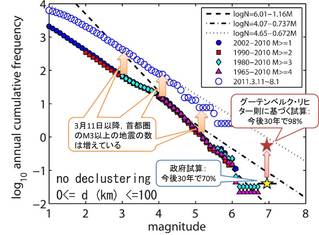
Ｍ３クラスの地震発生頻度が大震災後5.5倍になり、一日当たり1.48回になった。地震はＭが1大きくなると頻度が1/10になるという経験則が有り、これによって計算すると、そのような予測になるとのことでした。

単純に加減乗除の範囲で計算してみると、Ｍ7クラスの地震が18年に1回の比率で生じることになります。
従来は30年に1回と言われていたそうですから、頻度が大きくなったことを示していますが、4年以内に70％という数字とは違い過ぎます。

「18年」は周期ではありません。「18年に1回」も確率ではありません。
「4年以内に70％」という確率はどのように計算したら求まるのか、興味が有ります。

18年にしろ30年にしろ、それが確率過程の周期だとすれば、今直ぐ地震が起きる確率密度も0ではないという点では同じです。
もしかして、現に今、どこかで発生していて、もうすぐ此処も揺れ始めるかも。
真に受けて「今か、今か、・・・」と精神を集中して待ち受けるということを1分でも続けたら、心臓はドキドキし、治まっても不安神経症が後遺症として残りかねない・・・とまで考えたら過剰反応でしょうか。

確率をどのようにして計算したかが不明なら、注意を呼びかけた親切な予測があったと云うより、無用の混乱を招く間違った速報だったと言うべきでしょう。
18年どころか、30年以内にも直下型大地震は起きないと云う、もしかしたら脳天気な考え方を正すべき理由にならないと思うのです。

気象庁の観測データを基礎に、東大の地震研が計算し、そのホームページに公開してあると書いてあったので、検索してみましたが、見当たりませんでした。

仮に、地震発生の確率過程が例えばポワソン分布し、18年がそのパラメータだと云うように考えるとしても、4年間の累積確率が70％になるというのは大き過ぎます。
ポワソン分布は兵隊が馬に蹴られて死ぬという事故の発生頻度の研究から導かれたものだそうです。
ドイツから発射されたミサイルがロンドン市内に落下する分布に適用して評価され、今日では工業の品質管理などで良く利用されていると聞いたことが有ります。

地震発生の研究は地下の構造の変化との対応が最も重要でしょうから、定型の理論分布を仮定して素人でも計算できるようなものではないのでしょう。
そんな風に納得しようとしていたら、ようやくか、偶々か、
「2011年東北地方太平洋沖地震による首都圏の地震活動の変化について」と題したサイトが見つかりました。
http://outreach.eri.u-tokyo.ac.jp/eqvolc/201103_tohoku/shutoseis/

新聞報道には間違いが有ることを指摘し、実際の地震研の研究について紹介しています。
一連の報道は誤報に端を発し、各社からの問い合わせがあって、更に新たな誤解や中途半端な解釈を含んだものが速報とかとして流されることになったのだと知れます。
編集者はサイエンス・ライターに相談しなくても理解できることと思ったのでしょうか。
さすが専門家の言っていることとメディアの文章との間には大きな落差があります。
誤解は一度生じると再生産され、完全に正すことはいつも難しいと思います。

地震研の広報活動は「地震に備えろ」という警告に熱心なためか、データの意味するところについての説明はおろそかです。
掲載してあるグラフを見れば誰にでも理解できるだろうと言うことかも知れませんので転載します。
Ｍ４を境として発生頻度に異なる傾向があり、今後30年でのＭ７の試算には無理が有る、早い話が「間違いだ」と読み取れます。

コメント

  

 

 

 

 

• 
• 
• 
•