連立方程式 と グラフ ～ の 関係

中学２年になって、連立方程式 というものを習います。

連立方程式！

いかにも難しそうなこの 言葉のひびき！

分かってしまえば  たいしたことはないのですが・・・

実はこの連立方程式の 解（答えですね）は、

グラフに書いて求める方法も あったのです！

 

たとえば、Y＝２X－２    と    Y=－X＋４   の 連立方程式の解は

この２つの関数をグラフに書いて、それらが交差した点の

X座標と、Y座標が  連立方程式の 解 になります。

このグラフを書いてみますと、（２，２）の点で交差します。

これで、X=２，Y=２  と  解けるのです。

この交点の座標は、どちらの関数にも属しますので

この交点の座標が、２つの関数に共通のX と Y の値です。

 

このように、グラフを書いてすぐに分かる場合もあるのですが

X と Y の値が、整数ではない場合

これはもう式を計算するしかありません。

ということで、今回の問題は

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

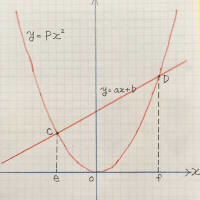
グラフ上に ４点 A（-2.-、-1）、B(5、6）、C（-2、7）、D（2、1）

が あります。

線分AB と 線分CD が 交差する点の座標を 求めましょう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

前置きが長かったので、迷ってしまうでしょうか？

作図か、計算か？

あなたなら どうする？