1次関数、傾きの 有効範囲とは？

前回の問題をもう一度読み返しますと

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

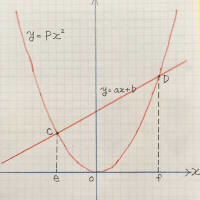
座標平面で、点A（-3、5）を通る直線を、 Y=ｍX＋ｎ とする。

この直線が ２点（-5、2）と（6、-1）を結ぶ線分（両端を含む）と

共有点を持つとき、ｍの取り得る値の範囲を求めなさい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

 

この文章は、どう考えたって日常会話の言葉づかいではないですね。

しかも、なんだか怒られてるみたいだし、上から目線だし・・・・

でも、この独特の表現は  暗号だと思えば 我慢もできるかも・・・

 

では、その暗号を解いていきましょう～

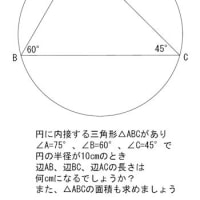
この問題は、1次関数の傾きの有効範囲を求める問題です。

前回ヒントに書きました座標に少し線を書いてみます。

（-3、5）を通る線は、無数にありますが、ためしに２本引いてみますと

Aの場合は、線分と交わらないので 共有点がありません。

Bの場合は、交わりますので OKですね。

では交点ができるギリギリのところを探して線を引きますと

このようになります。

と、このようになります。

 

今回の、暗号解き  すっきりしましたか？