素因数分解 と 平方根

平方根の問題が出るときに、よく使うのが

素因数分解！です

1つの数字を 素数の積に書き換えることです。

 

たとえば、１８０ を素因数分解すると

（小さな素数で順に割っていきます）

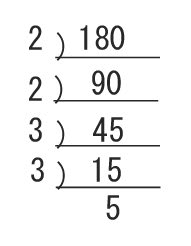
このように端からかじっていくような計算をして、１８０＝2×2×3×3×5

と、なります。

この他にも、

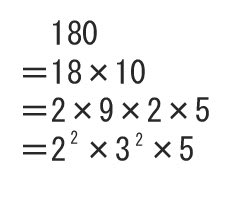
と、せんべいを割って食べるように、おおまかに割っていって求める方法

また、これと同じですが メモ書きするときに

と、このように葉っぱが広がるような図を描く方法などあります。

問題によりますが、出てくる最初の数字によっては

最初に何で割ったら割り切れるのか？分かりにくいものもあります。

偶数ならば２で割れますが、たとえば ４４１ という数字なら

最初に何で割ったら 割り切れるのか？

悩みますね～

こんな時は、数の各桁の数字を足して３の倍数になれば３で割り切れる！

という法則を使います。

４４１なら、  ４＋４＋１＝９  ９は３の倍数なので  ４４１は３で割り切れる！

と、分かります。

どんな大きな数字でも同じ！１４５７３１だと、各桁の数字の合計は２１

２１は ３の倍数なので、 １４５７３１は、３で割り切れます。

これは、便利な法則なので覚えておいて損はしないと思います～

 

また、平方根の問題で ルートの中にある数を素因数分解するときは

４（２の２乗）とか、９（３の２乗）とか、２５（５の２乗）とか、１００（１０の２乗）などで

割ることができれば、あとの計算が楽になります。

 

今回は、先にヒントを書きました。ここからが問題！（過去の入試問題より）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

２３４に３桁の自然数 ｎ をかけて、ある整数の２乗になるようにしたい。

このような３桁の自然数 ｎ のうち、最も小さい自然数を求めなさい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ところで、

数の各桁の数字を足して３の倍数になれば３で割り切れる！

どうしてなのか？わかりますか？